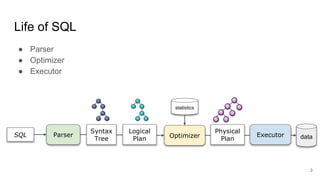
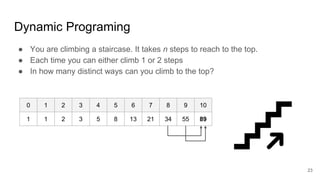
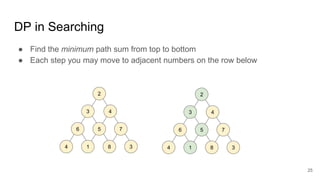
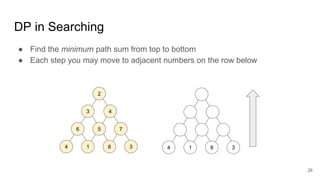
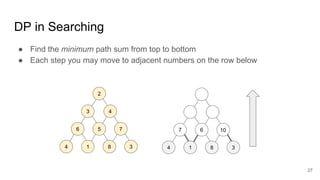
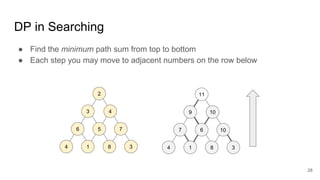
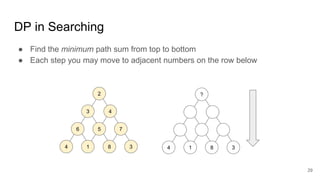
The document describes the Volcano/Cascades query optimizer. It uses dynamic programming to efficiently search the large space of possible query execution plans. The optimizer represents queries as logical and physical operators connected by transformation and implementation rules. It explores the logical plan space and then builds physical plans by applying these rules. The search is guided by estimating physical operator costs. The optimizer memoizes partial results to avoid redundant work. This approach allows finding optimal execution plans in a principled way that scales to complex queries and optimizer extensions.

1. The Volcano/Cascades Optimizer
Eric Fu
2018-11-14

2. Outline
● Background
● Dynamic Programming
● Components
● Search Engine
● Summary
2

3. Life of SQL
SQL Parser Optimizer Executor
Syntax
Tree
Logical
Plan
Physical
Plan data
● Parser
● Optimizer
● Executor
statistics
3

4. Query Optimization Strategies
● Choice #1: Heuristics
○ INGRES, Oracle (until mid 1990s)
● Choice #2: Heuristics + Cost-based Join Search
○ System R, early IBM DB2, most open-source DBMSs
● Choice #3: Randomized Search
○ Academics in the 1980s, current Postgres
● Choice #4: Stratified Search
○ IBM’s STARBURST (late 1980s), now IBM DB2 + Oracle
● Choice #5: Unified Search
○ Volcano/Cascades in 1990s, now MSSQL + Greenplum
4

5. Problem
● Why query optimizing is such a hard problem?
● It’s not difficult to find a feasible solution
● It’s almost impossible to find a optimal solution
5

6. Why So Many Choices?
● Equivalence Rules
● Various Implements
Join
Join D
Join C
A B
Join
JoinA
JoinB
DC
Join
Join
A
Join
B DC
ABCD, ABDC, ACBD, ACDB, ADBC, ADCB,
BACD, BADC, BCAD, BCDA, BDAC, BDCA,
CABD, CADB, CBAD, CBDA, CDAB, CDBA,
DABC, DACB, DBAC, DBCA, DCAB, DCBA
6

7. Why So Many Choices?
● Equivalence Rules
● Various Implements
HashJoin
NestedLoopJoin
SortMergeJoin
IndexScan
TableScan
Join
JoinA
JoinB
DC
In Total: 24 * 3 * 2^4 * 3^3 = 31104 !!!
7

8. Which one is better?
● Given a physical plan, we can estimate its total cost
● Cost of an operator is related to input rows
● Selectivity Factors
SELECT *
FROM Reviews
WHERE 7/1< date < 7/31 AND
rating > 9
8

9. Summary of Background
Good News
● We known how to construct the search space
Bad News
● It’s almost impossible to exhaust the search space
● We need an elegant & smart way to do the search
9

10. Dynamic Programing
in Algorithm
10

11. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
11

12. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1
12

13. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 2
13

14. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 2 3
14

15. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 2 3 5 8 13 21 34 55 89
15

16. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 ?
It’s fine to go reversely...
16

17. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 ? ?
17

18. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 ? ? ?
18

19. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 2 ? ? ? ?
19

20. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 2 ? ? ? ? ?
20

21. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 2 3 ? ? ? ?
21

22. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 2 3 5 ? ? ?
22

23. Dynamic Programing
● You are climbing a staircase. It takes n steps to reach to the top.
● Each time you can either climb 1 or 2 steps
● In how many distinct ways can you climb to the top?
0 1 2 3 4 5 6 7 8 9 10
1 1 2 3 5 8 13 21 34 55 89
23

24. Define Dynamic Programing (DP)
● DP is solving a problem by solving a sub-problem
● DP is only appliable for Optimal Substructure
○ Optimal solution of current solution can be calculated from optimal solution of sub-problems
● DP can be done in both directions
○ Filling a table
○ DFS with memo
24

25. DP in Searching
● Find the minimum path sum from top to bottom
● Each step you may move to adjacent numbers on the row below
2
3 4
6 5 7
4 1 8 3
2
3 4
6 5 7
4 1 8 3
25

26. DP in Searching
● Find the minimum path sum from top to bottom
● Each step you may move to adjacent numbers on the row below
2
3 4
6 5 7
4 1 8 3 4 1 8 3
26

27. DP in Searching
● Find the minimum path sum from top to bottom
● Each step you may move to adjacent numbers on the row below
2
3 4
6 5 7
4 1 8 3
7 6
4 1 8 3
10
27

28. DP in Searching
● Find the minimum path sum from top to bottom
● Each step you may move to adjacent numbers on the row below
2
3 4
6 5 7
4 1 8 3
9
7 6
4 1 8 3
10
10
11
28

29. DP in Searching
● Find the minimum path sum from top to bottom
● Each step you may move to adjacent numbers on the row below
2
3 4
6 5 7
4 1 8 3
?
4 1 8 3
29

30. Dynamic Programing
30

31. Apply DP in Optimization?
Sort
Join
A B
Sort
HashJoin
Scan A Scan B
SortMergeJoin
Scan B
SELECT * FROM A, B WHERE A.bid = B.bid ORDER BY A.bid
Scan A
Sort
Optimal Plan!
Order by aid
Order by bid
Order by bid
31

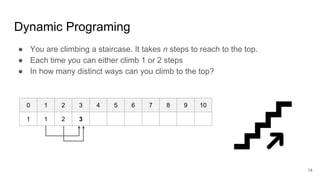
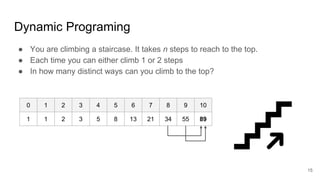
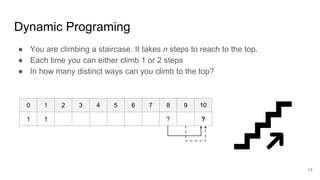
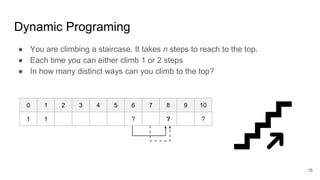
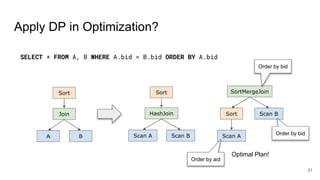
32. Apply DP in Optimization?
Sort
Join
A B
Sort
HashJoin
Scan A Scan B
SortMergeJoin
Scan B
Scan A
Sort
Optimal Plan of [AB]
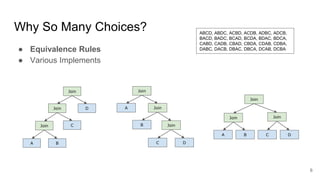
You cannot just apply DP straightforwardly
32

33. RelSet[ABCD]
System-R Optimizer
● Dynamic Programing
● Interesing Orders
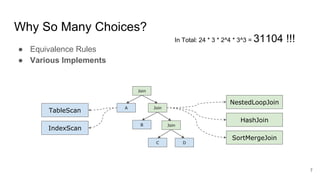
The main contribution: Optimal Substructure is defined so DP is feasible.
ABCD, ABDC, ACBD, ACDB,
ADBC, ADCB, BACD, BADC,
BCAD, BCDA, BDAC, BDCA,
CABD, CADB, CBAD, CBDA,
CDAB, CDBA, DABC, DACB,
DBAC, DBCA, DCAB, DCBA
Access Path Selection in a Relational Database Management System (SIGMOD 1979)
33

34. RelSet[ABCD]
System-R Optimizer
● Dynamic Programing
● Interesing Orders
The main contribution: Optimal Substructure is defined so DP is feasible.
SortBy[A]ASC SortBy[A]DESC SortBy[B]ASC
······ ··· ···
34

35. Optimal Substructures
● Based on assumption that cost function is polynomial
● Stores Best Plan for each pair of (Relation Set, Physical Properties)
● Instead of O(n!) plans, only O(n·2n-1) plans need to be enumerated.
RelSet[ABCD]
Order1 Order2 Order3
RelSet[ABC]
Order1 Order2 Order3
RelSet[BCD]
Order1 Order2 Order3
Goal
35

36. Volcano/Cascades Optimizer (1993)
● Implemented as a code generator (operators, rules, etc) and dynamic-link
library (the search engine)
● Top-down Search (Directed Search)
○ Start with the final outcome that you want
○ Search path could be guided by heuristics
● Relatively, System-R’s approach is in bottom-up style
36

37. Graefe Goetz
● Volcano - An Extensible and Parallel Query
Evaluation System (1990)
● The Volcano Optimizer Generator: Extensibility and
Efficient Search (1991)
● The Cascades Framework for Query Optimization
(1995)
37

38. Components
Operators
● logical operators
● algorithms
● enforcers
Rules
● transformation rules
● implementation rules
Properties
● logical properties
● physical properties
Interfaces of Operators
● property function
● applicability function (physical-only)
● cost function (physical-only)
38

39. Operators
● logical operators
○ e.g. Join, Scan
● algorithms
○ e.g. HashJoin, SortMergeJoin, FileScan, IndexScan
● enforcers
○ e.g. Sort, Shuffle
39

40. Rules
● transformation rules
○ Tha algebraic rules of expression equivalence
○ e.g. associativity rule, commutative rule
● implementation rules
○ Rules mapping logical operator to algorithms
○ Possible to map multiple logical operators to a single physical operator
● Specify how to match rules to plan tree
○ Sime pattern matching
○ Other condition code is also allowed
40

41. Properties
● logical properties
○ Can be derived from the logical algebra expression
○ Attached to logical equivalent set: [LogExpr]
○ e.g. schema, expected size
● physical properties
○ Depend on algorithms
○ Attached to physical equivalent set: [LogExpr, PhyProp]
○ e.g. sort order, partitioning
physical properties vector
41

42. Interfaces of Operators
● applicability function
○ Physical property vectors that it can deliver with
○ Physical property vectors that its input must satisfy
● cost function
○ Estimate its cost
○ Cost is an abstract data type in Volcano. e.g. (CPU cost, IO cost)
● property function
○ Determine logical properties e.g. schema, row count
■ selectivity estimate
○ Determine physical properties e.g. sort order
only applicable for
algorithms & enforcers
42

43. Components
Operators
● logical operators
● algorithms
● enforcers
Rules
● transformation rules
● implementation rules
Properties
● logical properties
● physical properties
Interfaces of Operators
● property function
● applicability function (physical-only)
● cost function (physical-only)
43

44. Search Engine
Define goal as [LogExpr, PhysProp]
Logically we may divide the searching procedure into 2 stages:
1. Explore: Apply transformation rules to explore expression space
2. Build: Apply implementation rules to build physical plans and find best one
44

45. Explore
● Apply transformation rules to explore expression space
● e.g. [ABC] = { (A⨝B)⨝C, (B⨝A)⨝C, (A⨝C)⨝B …}
Join
Join C
A B
Join
Join C
B A
Join
JoinA
CB
Join
JoinC
AB
····
Generated Logical PlansGoal.LogExpr
45

46. Build
● Apply implementation rules to build physical plans
● For every [LogExpr, PhyProp] record the physical plan to Memo table
● e.g. [AB]⨝C ➡ SortMergeJoin v.s. HashJoin
LogExpr PhyProp BestPlan
[ABC]
-
x⬆
x⬇
[AB] -
… …
Memo Table
HashJoin
[AB] Scan(C)
SMJ
Scan(C)
[AB]
Sort
SMJ
Scan(C)[AB] x⬆
Total Cost = ? Total Cost = ? Total Cost = ?
46

47. Some Facts
● Volcano do Explore then Build
● While Cascades have only one stage
Actually exploring almost happens before building even in Cascades. Why?
47

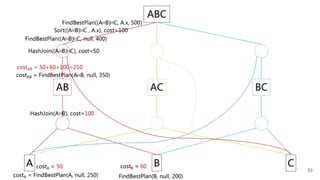
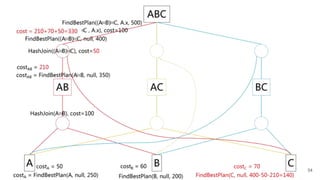
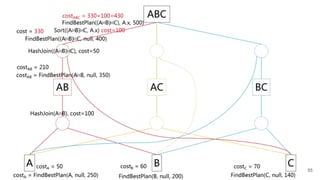
48. Example
Logical Expression Space:
[ABC]
[AB], [AC], [BC]
[A], [B], [C]
Our Mission:
FindBestPlan((A⨝B)⨝C, A.x, 500)
Logical Expression Order Limit
48

49. 49

50. 50

51. 51

52. 52

53. 53

54. 54

55. 55

56. 56

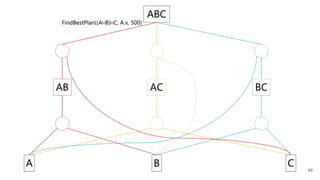
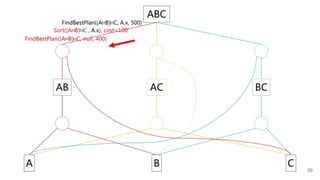
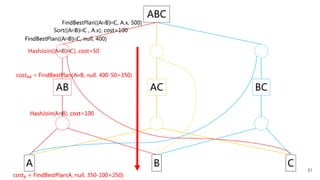
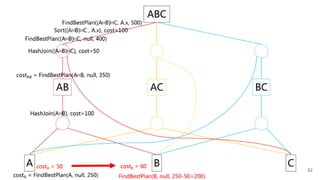
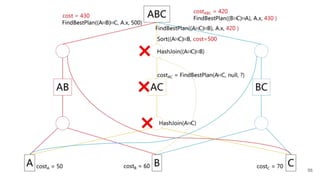
57. FindBestPlan(LogExpr, PhysProp)
If Memo[LogExpr, PhysProp] is not empty:
● return BestPlan or Failures
Possible moves =
● applicable transformations
● algorithms that give the required PhysProp
● enforcers for required PhysProp
ForEach (Move = pop the most promising moves)
● is transformation: Cost = FindBestPlan(LogExpr, PhysProp)
● is algorithm: Cost = Costself + Sum(Costinput)
● is enforcer: Cost = Costself + Costinput
Memo[LogExpr, PhysProp] = Best Plan
return Best Plan
57

58. Some Details
● Use cost limit to do branch-and-bound pruning
○ By default set to unlimited
● Mark (LogExpr, PhysProp) as in-progress to prevent dead loop
○ e.g. A JOIN B <=> B JOIN A
● Use prioirity queue to do heuristic ordering of moves
○ Calcite prioritizes RelSet with less depth and higher cost
58

59. Summary
Volcano/Cascades Optimizer …
● use Rules to build all logical or physical plans
● use Cost to evaluate a physical plan
● use Dynamic Programming to search for the optimal physical plan
59

60. Compared with RBO
Here are my personal opinions …
● Cost-based: Could find better physical plans
● Rule-independent: Provide an elegant interface for DB implementors
● Still Heuristic: May performs bad in some corner cases
60

61. Thanks!
Q&A