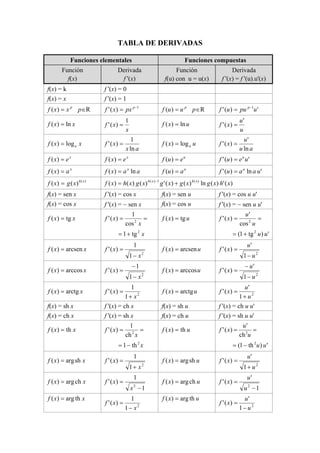
The document contains a table of derivatives that lists common functions and their derivatives. It provides the derivative formulas for elementary functions like polynomials, logarithms, exponentials, trigonometric functions, inverse trigonometric functions, hyperbolic functions, and inverse hyperbolic functions. It also includes the chain rule for finding the derivative of composite functions where the inner function is composed of x.

1. TABLA DE DERIVADAS
Funciones elementales
Funciones compuestas
Función
f(x)
Derivada
f '(x)
Función
f(u) con u = u(x)
Derivada
f '(x) = f '(u).u'(x)
f(x) = k
f '(x) = 0
f(x) = x
f '(x) = 1
pxxf=)( p∈R
1)('−=ppxxf
puuf=)( p∈R
' )('1upuufp−=
xxfln)(= xxf1)('=
uxfln)(= uuxf')('=
xxfalog)(= axxfln1)('=
uxfalog)(= auuxfln')('=
xexf=)(
xexf=)(
ueuf=)(
' )('ueufu=
xaxf=)(
aaxfxln)(=
uauf=)(
' ln)('uaaufu=
)()()(xhxgxf= ) (' )(ln)()(')( )()()(1)(xhxgxgxgxgxhxfxhxh+=−
f(x) = sen x
f '(x) = cos x
f(x) = sen u
f '(x) = cos u u'
f(x) = cos x
f '(x) = − sen x
f(x) = cos u
f '(x) = − sen u u'
xxftg)(= == xxf2cos1)('
x2tg1+=
uxftg)(= == uuxf2cos')('
' )tg1(2uu+=
xxfarcsen)(= 211)(' xxf− =
uxfarcsen)(= 21')(' uuxf− =
xxfarccos)(= 211)(' xxf− − =
uxfarccos)(= 21')(' uuxf− − =
xxfarctg)(= 211)(' xxf+ =
uxfarctg)(= 21')(' uuxf+ =
f(x) = sh x
f '(x) = ch x
f(x) = sh u
f '(x) = ch u u'
f(x) = ch x
f '(x) = sh x
f(x) = ch u
f '(x) = sh u u'
xxfth )(= == xxf2ch1)('
x2th1−=
uxfth )(= == uuxf2ch')('
' )th1(2uu−=
xxfsh arg)(= 211)(' xxf+ =
uxfsh arg)(= 21')(' uuxf+ =
xxfch arg)(= 11)(' 2− = xxf
uxfch arg)(= 1')(' 2− = uuxf
xxfth arg)(= 211)(' xxf− =
uxfth arg)(= 21')(' uuxf− =