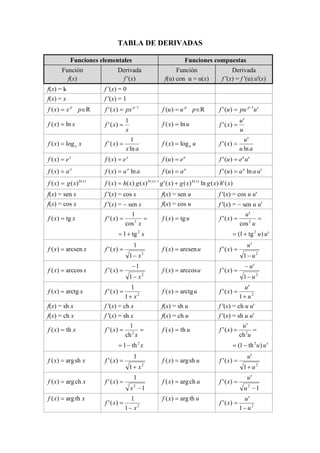
This table summarizes the derivatives of common elementary and composite functions. For elementary functions, the derivative is given. For composite functions f(u) with u = u(x), the derivative is the derivative of the inner function u' multiplied by the derivative of the outer function evaluated at u.

1. TABLA DE DERIVADAS
Funciones elementales Funciones compuestas
Función
f(x)
Derivada
f '(x)
Función
f(u) con u = u(x)
Derivada
f '(x) = f '(u).u'(x)
f(x) = k f '(x) = 0
f(x) = x f '(x) = 1
p
xxf =)( p∈R 1
)(' −
= p
pxxf p
uuf =)( p∈R ')(' 1
upuuf p−
=
xxf ln)( =
x
xf
1
)(' = uxf ln)( =
u
u
xf
'
)(' =
xxf alog)( =
ax
xf
ln
1
)(' = uxf alog)( =
au
u
xf
ln
'
)(' =
x
exf =)( x
exf =)( u
euf =)( ')(' ueuf u
=
x
axf =)( aaxf x
ln)( = u
auf =)( 'ln)(' uaauf u
=
)(
)()( xh
xgxf = )(')(ln)()(')()()( )(1)(
xhxgxgxgxgxhxf xhxh
+= −
f(x) = sen x f '(x) = cos x f(x) = sen u f '(x) = cos u u'
f(x) = cos x f '(x) = − sen x f(x) = cos u f '(x) = − sen u u'
xxf tg)( = ==
x
xf 2
cos
1
)('
x2
tg1+=
uxf tg)( = ==
u
u
xf 2
cos
'
)('
')tg1( 2
uu+=
xxf arcsen)( =
2
1
1
)('
x
xf
−
= uxf arcsen)( =
2
1
'
)('
u
u
xf
−
=
xxf arccos)( =
2
1
1
)('
x
xf
−
−
= uxf arccos)( =
2
1
'
)('
u
u
xf
−
−
=
xxf arctg)( = 2
1
1
)('
x
xf
+
= uxf arctg)( = 2
1
'
)('
u
u
xf
+
=
f(x) = sh x f '(x) = ch x f(x) = sh u f '(x) = ch u u'
f(x) = ch x f '(x) = sh x f(x) = ch u f '(x) = sh u u'
xxf th)( = ==
x
xf 2
ch
1
)('
x2
th1−=
uxf th)( = ==
u
u
xf 2
ch
'
)('
')th1( 2
uu−=
xxf sharg)( =
2
1
1
)('
x
xf
+
= uxf sharg)( =
2
1
'
)('
u
u
xf
+
=
xxf charg)( =
1
1
)('
2
−
=
x
xf uxf charg)( =
1
'
)('
2
−
=
u
u
xf
xxf tharg)( =
2
1
1
)('
x
xf
−
=
uxf tharg)( =
2
1
'
)('
u
u
xf
−
=