The document discusses parallelizing image processing algorithms for effective image analysis. It aims to design parallel algorithms for common image processing tasks like filtering and edge detection to reduce processing time. The key aspects of parallel algorithm design discussed are partitioning, communication, agglomeration, and mapping tasks to processors. Performance analysis metrics like Amdahl's law and Gustafson-Barsis' law are also covered to understand speedup from parallelization and ensure algorithms remain cost effective as the number of processors increases.

1. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
PARALLELIZATION OF IMAGE PROCESSING
ALGORITHMS FOR EFFECTIVE IMAGE
ANALYSIS
S.M. Jaisakthi
September 9, 2009

2. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Research Motivation
Research Motivation
Image processing is the technique used to manipulate the
image in order to enhance, restore or interpret the image.
Sequential.
Computationally intensive.
Hence image analysis algorithms need more response time and
lack scalability.

3. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Research Motivation
Research Motivation
These issues can be solved by parallelizing the existing sequential
algorithms by exploiting the massive computational power of the
parallel computers.

4. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Research Motivation
Research Objective
Research Objective
To design parallel algorithms for image processing operations such
as filtration, histograms, edge detection, image segmentation etc.,
cost effectively in terms of reduced parallel overheads and applying
these algorithms for effective parallelization of image analysis
applications.

5. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Parallel Algorithm Design
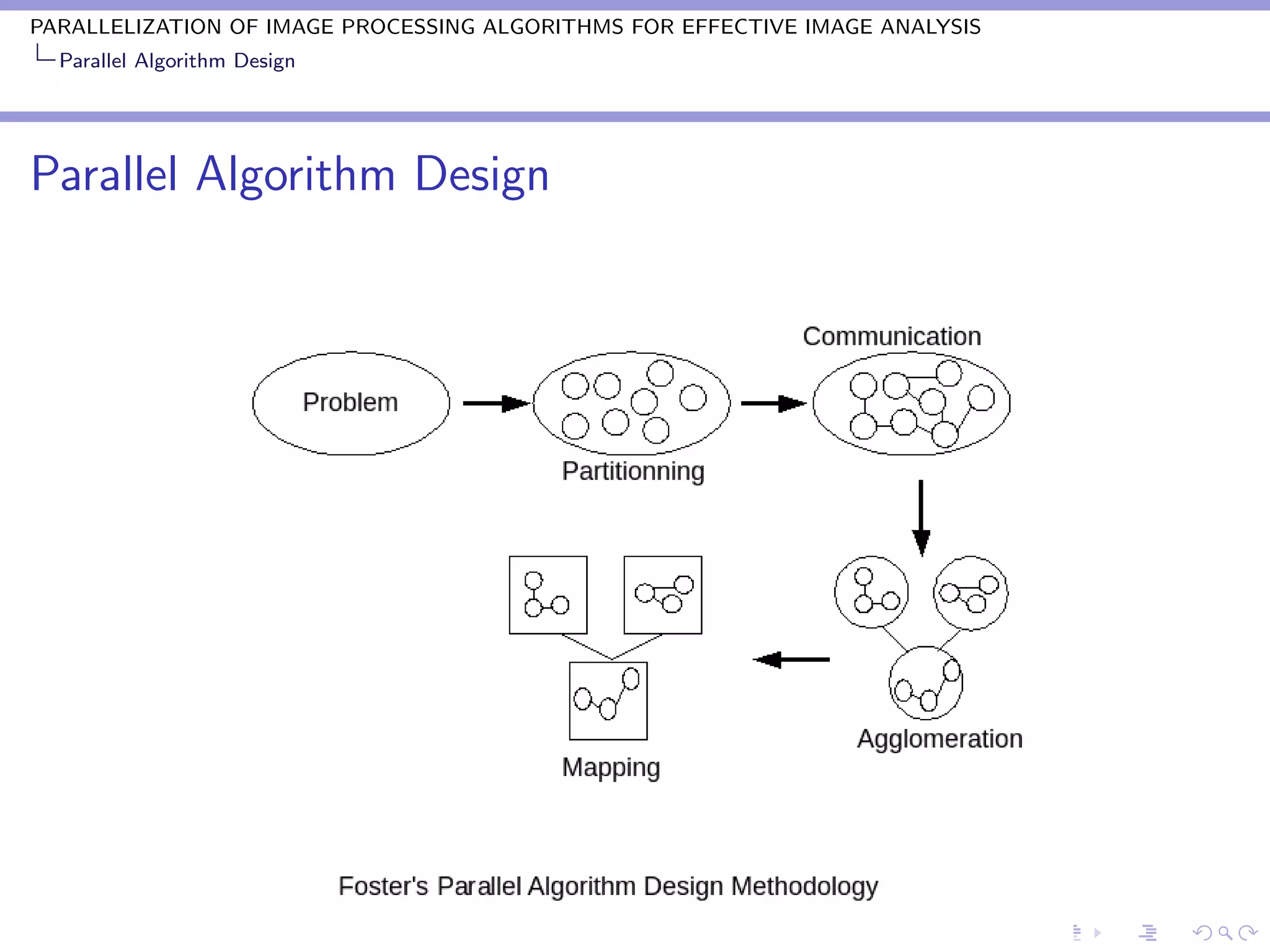
Parallel Algorithm Design
According to Foster the design of parallel algorithm consist of 4
stages[13] :
Partitioning
Communication
Agglomeration
Mapping

6. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Parallel Algorithm Design
Parallel Algorithm Design

7. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Parallel Algorithm Design
Partitioning
Partitioning
Decompose given problem into primitive task.
Domain Decompositon
Divide data into pieces
Determine how to associate computations with the data
Functional Decomposition
Divide computation into pieces
Determine how to associate data with the computations
Design Strategy
Redundant computation and redundant data structure storage
are minimized.
Tasks are roughly same size.
Number of tasks is an increasing function of problem size.

8. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Parallel Algorithm Design
Communication
Communication
Determine communication structure between tasks.
Local Communication
Global Communication
Design Strategy
Communication operations are balanced among Tasks.
Each Task communicate with only small group of neighbours.
Tasks can perform communications concurrently.
Tasks can perform computations concurrently.

9. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Parallel Algorithm Design
Agglomeration
Agglomeration
Combining task into larger task.
Goal
Reduces the communication overheads.
Maintains scalability.
Reduces software engineering cost.
Design Strategy
Replicated computations take less time.
Agglomerated tasks have similar computational and
communications costs.

10. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Parallel Algorithm Design
Mapping
Mapping
Process of assigning task to processors.
Goal
Maximize processor utilization
Minimize Interprocessor Communication.
Design Strategy
One task per processor and multiple task per processor design
have been considered

11. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Performance Analysis
Understand the barriers to higher performance.
Calculates how much improvement can be obtained by
increasing number of processors.
Performance can be analysised using
Amdahl’s Law
Gustafson-Barsis’s Law
The Karp-Flatt Metric
Isoefficiency Metric

12. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Cost Effectiveness of a Parallel Algorithm
The cost of a parallel algorithm is the product of its run time
Tp and the number of processors used p.
A parallel algorithm is cost optimal when its cost matches the
run time of the best known sequential algorithm Ts for the
same problem.
SequentialExecutionTime
Speedup S = ParallelExecutionTime
Speedup
Efficiency ε = Numberofprocessorsused
A cost optimal parallel algorithm has speed up p and
efficiency 1.

13. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Amdahl’s Law
Amdahl’s Law
If F is the fraction of a calculation that is sequential, and (1-F) is
the fraction that can be parallelised, then the maximum speedup
that can be achieved by using P processors is
1
(1−F )
F+ p
Shows how execution time decreases as number of processors
increases.
Provides maximum speedup required to solve fixed size
problem with respect to number of processors.
Limitations
Ignores parallel overhead - overestimates speedup
Assumes problem as fixed size, so underestimates speedup
achievable

14. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Amdahl’s Effect
Amdahl’s Effect
As the problem size increases, the inherently sequential
portion decreases
As the problem size increases, computation dominates the
communication
As the problem size increases, the speedup increases

15. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Gustafson-Barsis’s Law
Gustafson-Barsis’s Law
Given a parallel program solving a problem of size n using p
processors, let s denote the fraction of total execution time spent in
serial code. The maximum speedup ψ achievable by this program is
ψ ≤ p + (1 − p)s

16. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Gustafson-Barsis’s Law
Gustafson-Barsis’s Law
Begin with parallel execution time
Estimate sequential execution time to solve same problem
Problem size is an increasing function of p
Predicts scaled speedup

17. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Karp-Flatt Metric
The Karp-Flatt Metric
Amdahls Law and Gustafson-Barsis Law ignore
Communication overhead
They can overestimate speedup or scaled speedup
Karp and Flatt proposed another metric

18. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Experimentally Determined Serial Fraction
Experimentally Determined Serial Fraction
Given a parallel computation exhibiting speedup Ψ on p processors,
where p ≥ 1, the experimentally determined serial fraction e is
defined to be the Karp - Flatt Metric
1 1
ψ
−p
e= 1
1− p
Takes into account parallel overhead
Detects other sources of overhead or inefficiency ignored in
speedup model
Process startup time
Process synchronization time
Imbalanced workload
Architectural overhead

19. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Isoefficiency Metric
Isoefficiency Metric
Scalability of a parallel system: measure of its ability to
increase performance as number of processors increases
A scalable system maintains efficiency as processors are added
Isoefficiency: Measures scalability

20. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Isoefficiency Metric
Isoefficiency Metric
In order to maintain the same level of efficiency as the number of
processors increases, n must be increased so that the following
inequality is satistied :
T (n, 1) ≥ CT0 (n, p)
where
ε(n,p)
C = (1−ε(n,p))
T0 (n, p) = (p − 1)σ(n) + pk(n, p)

21. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Isoefficiency Metric
References
Amir Hosein Kamalizad, Chengzhi Pan, Nader Bagherzadeh: Fast
Parallel FFT on a Reconfigurable Computation Platform.
SBAC-PAD 2003: 254-259
Bruno Galile, Franck Mamalet, Marc Renaudin, Pierre-Yves
Coulon: Parallel Asynchronous Watershed Algorithm-Architecture.
IEEE Trans. Parallel Distrib. Syst. 18(1): 44-56 (2007)
Chan, K.L.Tsui, W.M.Chan, H.Y.Wong, H.Y.Lai, H.C.,
Parallelising image processing algorithms, IEEE Region 10
Conference on Computer, Communication, Control and Power
Engineering, 1993, Vol. 2, PP. 942-944.
Cristina Nicolescu, Pieter Jonker: EASY PIPE: An “EASY to use”
Parallel Image processing Environment based on algorithmic
skeletons. IPDPS 2001:

22. PARALLELIZATION OF IMAGE PROCESSING ALGORITHMS FOR EFFECTIVE IMAGE ANALYSIS
Performance Analysis
Isoefficiency Metric
THANK YOU