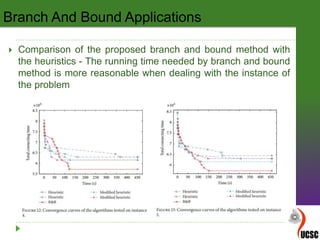
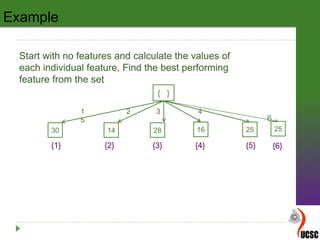
This document discusses feature selection algorithms and self-organizing maps (SOM). It begins by introducing concepts related to feature selection, including the curse of dimensionality and feature reduction. It then provides details on the branch and bound algorithm for feature selection, including its steps, properties, and an example application. Finally, it discusses the beam search algorithm for feature selection as an alternative to branch and bound, comparing their observations and recommendations.


































































![ A two‐layer network - A two‐dimensional input and m
output neurons
Two dimensional input
- defines the coordinates of the waste disposal sites (WDS) in
the two dimensional Euclidian space
- are fully connected to every output neuron
To get the scaled coordinates for WDS, range [0‐1] was
performed using the equation
SOM Algorithm To solve TSP problem - Steps](https://image.slidesharecdn.com/dataanalyticsconcepts-170804104816/85/Data-analytics-concepts-69-320.jpg)










![[1]"A Branch and Bound Algorithm for the Exact Solution of the Problem of
EMU Circulation Scheduling in Railway Network", Hindawi, 2015.
[2]"Beam-ACO—hybridizing ant colony optimization with beam search: an
application to open shop scheduling", ELSEVIER, 2017.
[3]"Kohonen Self-Organizing Map for the Traveling Salesperson Problem",
2017.
References](https://image.slidesharecdn.com/dataanalyticsconcepts-170804104816/85/Data-analytics-concepts-80-320.jpg)