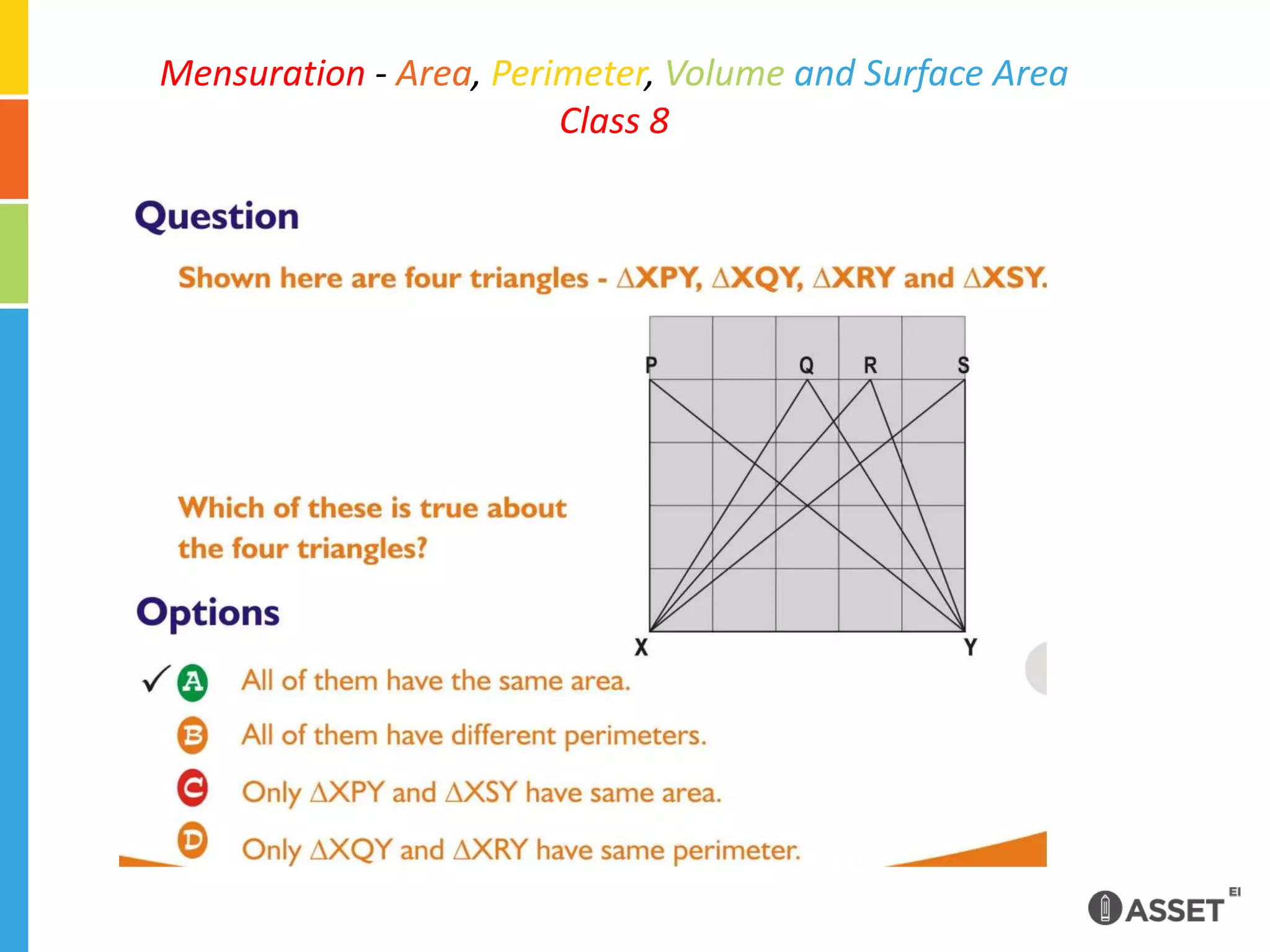
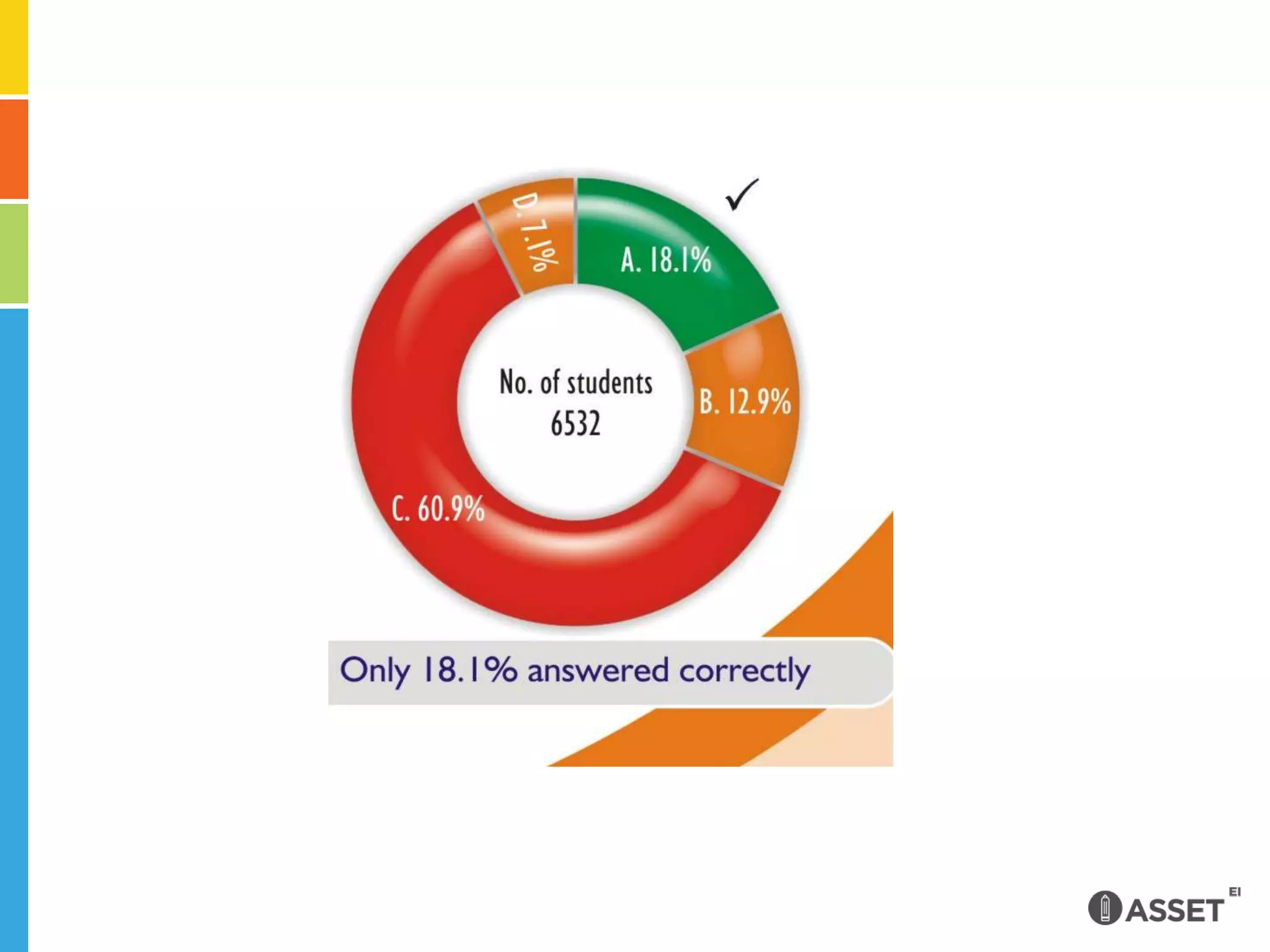
The document discusses a math assessment question about the areas of four right-angled triangles with the same base. Most students incorrectly answered that the triangles had different areas, likely because the altitudes were not drawn and they failed to visualize them. To improve understanding, teachers should expose students to more open-ended problems and facilitate discussion to investigate their reasoning, such as computing areas directly or applying the concept of congruent triangles.

1. Student MisconceptionsinMATHS – Part 6

2. Do your Student Learn or Mug up ?Students of all ages seem to have a mind of their own when it comes to responding to any situation or performing any task.As teachers, most of us go back home thinking that our students have understood every concept that we teach them. It is only when we test them that we find that some concepts have not been understood as clearly as they should have been.It is this desire to understand student thinking that prompted us to examine ASSET questions of the past rounds, in Maths, examining the most common wrong answers to understand what could have made students select the options they did.

3. Mensuration - Area, Perimeter, Volumeand Surface Area Class 8

5. Why was the question asked?The question checks if students understand that different triangles with the same base and height, would have the same area (a corollary of a formula they are familiar with i.e. area of a triangle = × base × height)What did students answer?Only 18% of students answered A, correctly. 61% chose the most common wrong answer, C.Possible reason for choosing B: These students probably felt that all the 4 triangles are not congruent to each other, and so concluded that they have different perimeters. They don’t seem to have noticed that DXPY and DXSY are congruent and so have the same perimeter.Possible reason for choosing C: These students may have seen that the given right angled triangles are congruent or may have computed their areas, to conclude that their areas are the same. These students have not been able to see that the areas of DXQY and DXRY are also equal (i.e. areas of all 4 triangles are equal), probably because the altitudes are not drawn, and they fail to visualize them.Possible reason for choosing D: Very few students have selected this option and are most probably making a random guess.

6. LearningsFor the given question, students could have done the following: Step 1: See that the base of all the given 4triangles is the same. Since area of triangle is × base × height, comparing their areas involves only comparing their altitudes. Step 2: The altitudes of all the triangles are equal, so the areas are also equal. They could also take the smallest squares on the grid as unit squares and actuallycompute areas to answer this question as shown here. The response data show that they were unable to analyze the question and solve it by taking any of the two approaches. They seem to have taken the easy way out to conclude that DXPY and XSY have the same area. They are also going purely by visual appearance to conclude that DXQY and DXRY have different areas. As the side lengths and altitudes are not mentioned explicitly, students have failed to compute the actual areas/perimeters. While it is important to develop proficiency with formulae and procedures, being able to see patterns that they imply leads to a deeper understanding and is also enriching and motivating to students.

7. 4. How do we handle this?The teacher may expose the students to open-ended problems like the ones given as opposed to routine drill problems.Activity 1: Give them this ASSET question. Investigate the strategies students adopt to solve the problem. You may facilitate the process by posing the following questions:• What can be said about the areas and perimeters of DXPY and DXSY? (Investigate if students are actually computing the areas/perimeters or are using the notion of congruence to infer their areas/perimeters being identical.)• What are areas of DXQY and D XRY?Also, • If students have been exposed to Pythagorean Theorem earlier, ask them to determine perimeters of DXQY and DXRY.• Ask them to draw at least one more triangle in the given grid having the same area as the given triangles.• Ask them to draw at least one more triangle in the given grid having the same perimeter as that of DXRY. (Check if students can apply the notion of congruence of triangles.)

8. THANKYOU(www.ei-india.com)