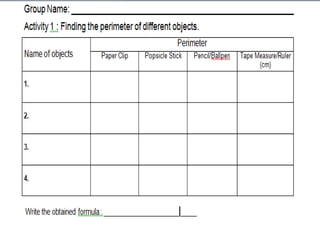
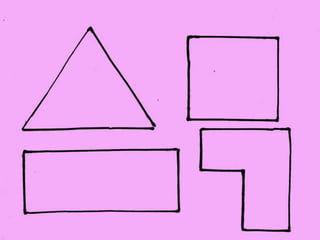
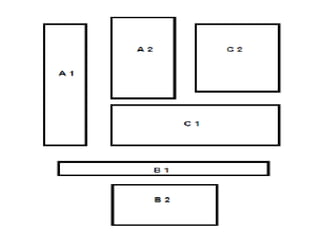
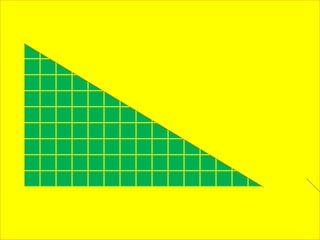
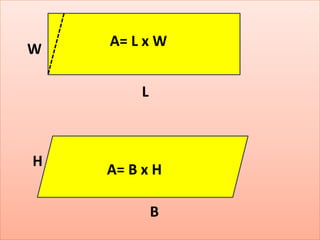
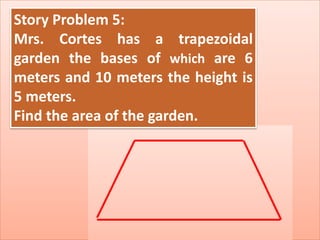
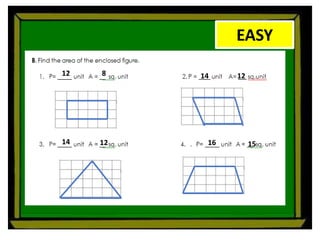
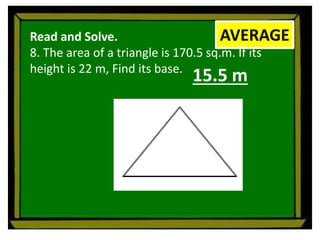
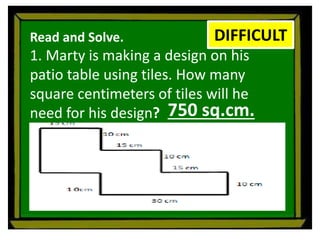
The document defines perimeter and area. Perimeter is a one-dimensional length measured in units like meters, while area is a two-dimensional measurement expressed in square units like square meters. Some issues students face in learning about area and perimeter are seeing them as just formulas, mixing up the concepts, not understanding standard units, and not linking mathematical concepts to real-world experiences. The document then describes activities to help students learn about perimeter and area through measuring real objects, finding perimeters and areas of shapes, decomposing complex figures, and solving word problems.

3. DEFINITION OF TERMS
PERIMETER
 comes from the Greek words peri (which
means around) and meter (which means
measure).
 is a length, which is one-dimensional and
measured in units of length such as meters,
centimeters or inches.

4. DEFINITION OF TERMS
AREA
 the amount of space inside the boundary of a
flat (2-dimensional) object.
https://www.mathsisfun.com/definitions/area.html
 is the number of unit squares equal in measure
to the surface.
 is measured in squares with bases of a certain
length and hence is expressed in two-dimensional
units such as m² (meters squared or square
meters).

5. ISSUES WITH LEARNING ABOUT AREA
AND PERIMETER
1. They may see area, and also sometimes
perimeter, as purely an application of
formulae without understanding what
area and perimeter actually are.
2. They sometimes mix up the concepts of
area and perimeter.

6. ISSUES WITH LEARNING ABOUT AREA
AND PERIMETER
3. They might not have the experience of
measuring with unconventional/non-
standard units of measurement such as
hands, twigs, etc. and therefore do not
know why it is better to use standard
units of measurement – for example
using meters instead of hand-spans,
which vary between individuals.

7. ISSUES WITH LEARNING ABOUT AREA
AND PERIMETER
4. They have difficulty developing an
understanding of dimension. Often,
they do not understand that perimeter
is a length, which is one-dimensional
and measured in units of length while
area is measured in square units and is
expressed in two-dimensional units such
as m².

8. ISSUES WITH LEARNING ABOUT AREA
AND PERIMETER
5. They may not link their everyday
experiences and intuitive understanding
of area and perimeter to what they
learn in the mathematics classroom.
www.TESS-India.edu.in
Teacher’s Guide – General Suggestions: Growing Up with
Math (4th Edition)

10. Activity 1: Finding the perimeters of objects
that surround us.
Procedures:
1. Find the perimeter (measure the length and
width) of at least 3 objects around the classroom
using non-standards and standard units (e.g.
paper clips, pencils, tape measure or ruler cm.)
2. Write the perimeter on the activity sheet
provided.

12. Activity 2: Finding the perimeters of
different polygons
Materials: Grid paper, cut outs of different polygons
Procedures:
1. Place 1 cut out of a polygon on a grid paper. Count
the number of units on each side.
2. Calculate the perimeter of each polygon. Write the
perimeter on the respective polygons.
3. Derive the formula of the perimeter of each polygon.

14. Activity 3: Working out the area of shapes using the
counting of squares method.
Materials: Cut outs of rectangles with different sizes, grid paper
Procedures:
1. Compare and manipulate the different cut outs of rectangle.
Arrange the rectangles according to their area (least to greatest).
2. Next, find the area of the rectangles using the grid paper. Trace
the rectangles on the grid paper and shade the squares covered by
the rectangles . Get the area of each rectangle by counting the
number of squares shaded then write the area on the rectangles.
3. Compare the areas of various rectangles, e.g. A1 < A2.
4. Using the length and width, derive the formula for the area of
rectangle.

16. Activity 4: Finding the area of different
polygons using grid paper.
Procedures:
1. Facilitator will provide story problems.
2. Visualize the given story problem using grid
paper.
3. Compute the area of polygons based on
your drawing
4. Derive the formulas for the areas of
different polygons.

17. Story Problem 1:
Nica has a square handkerchief
measuring 4 cm on each side. Find the
area of the handkerchief.
Story Problem 2:
The length and width of Marc’s
vacant lot are 6 m and 3 m respectively.
What is the area of Marc’s vacant lot?

18. Story Problem 3:
Mr. Torres has a
triangular field of palay
whose base is 15 meters
and whose height is 9
meters. Find the area of the
triangular field.

22. Roy planted vegetables in his
backyard to prevent soil erosion. His
vegetables garden is a
parallelogram. It has a base of 6
meters and a height of 4 meters.
What is the area of vegetable
garden?

25. W
L
A= L x W
A= B x H
H
B

26. Story Problem 5:
Mrs. Cortes has a trapezoidal
garden the bases of which are 6
meters and 10 meters the height is
5 meters.
Find the area of the garden.

28. Activity 5: Finding the Areas of Complex
Figures
Procedures:
1. Find the area of large, rectilinear figure by
decomposing it into smaller rectangles.
2. Label the dimensions of the rectangles.
3. Find the area of the figure. (see the
figures in the activity sheets)

31. EASY
48 cm
17 cm
10 cm
36 cm

32. EASY
12 8 14 12
14 12 16 15

33. EASY
Read and Solve.
1. A rectangular place mat is 45 cm long
and 30 cm wide. What is its a.
perimeter? _______ b. area? _____
2. A table runner is shaped like an isosceles
triangle. The base is 90 cm and each of the
equal sides is 50cm. How much lace can be
placed around it?
150 cm 1350 cm2
190 cm

34. EASY
Read and Solve.
3. When the perimeter of a regular polygon is divided
by 5, the length of a side is 25 cm. What is the name
of the polygon?
What is the perimeter?
pentagon
125 cm

35. EASY
Read and Solve.
4. The Mathematics Club was given a small lot 9m by
6 m in the school yard to be made into a
mathematics garden.
a. If the officers wish to fence it, how much wire will
they need?
b. What is the area of the lot?
5. A rectangular lawn is 28 m by 12 m. If you walk
around it, how many meters will you walk?
30 m
54 sq.m
80 m

36. Read and Solve.
1. A rectangular garden is 12 m wide. If the
length is 5m longer than its width what
is its perimeter?
What is its area?
AVERAGE
58 m
204 sq.m

37. Read and Solve.
1. The triangular front of a cabin has a base
of 9m and a height of 5m . What is the area
of the front part of the cabin?
3. The height of a rectangular blackboard is
half the length of the blackboard. Find its
area if the length is 11 meters.
AVERAGE
22.5 sq.m
60.5 sq.m

38. Read and Solve.
4. What is the area of a trapezoid with
bases 2.4 cm and 5.6 cm and a height of
4.2 cm?
AVERAGE
16.8 sq.m

39. Read and Solve.
5. A football square field is 400 sq. meters
and has to be enclosed by a fence.
a. Find the length of a side of the
football field.
b. How much fencing material will be
needed to enclose the football field?
AVERAGE
20 m
80 m

40. Read and Solve.
6. A picture measures 15 cm by 18 cm. It is
placed on a colored cardboard where 3 cm
of the card board is seen around the
picture. What area of the card board is
seen?
AVERAGE
234 sq. m

41. Read and Solve.
7. Four equal squares are placed side by
side as shown. The perimeter of the
rectangle formed is 150 centimeters. Find
the area of each square.
AVERAGE
225 sq.cm

42. Read and Solve.
8. The area of a triangle is 170.5 sq.m. If its
height is 22 m, Find its base.
AVERAGE
15.5 m

43. Read and Solve.
9. What is the relation of the area of a triangle
to the area of a parallelogram if they have the
same base and height?
AVERAGE
The area of a triangle is ½ the area of the
Parallelogram Or the area of a parallelogram
is twice the area of the triangle

44. Read and Solve.
10. A subdivision lot is shaped like a
trapezoid. If the parallel sides measure 53.7 m
and 78.4 m and bases are 30.2 m apart, what
is the area of the lot?
AVERAGE
3989.42 sq.m

45. Read and Solve.
1. Marty is making a design on his
patio table using tiles. How many
square centimeters of tiles will he
need for his design?
DIFFICULT
750 sq.cm.

46. Read and Solve.
2. A garden measures 12 feet by 10
feet. It is surrounded by a walkway
that is 2 feet wide. Find the area of ;
a) the garden -
b) the walkway,
a) the entire space.
DIFFICULT
120 sq.ft.
104 sq.ft.
224 sq.ft.

47. Read and Solve.
3. Mario has 48 meters of fencing
material.
a. He plans to make a rectangular
garden whose dimensions are whole
numbers. How many different garden
can he make?
b. Mario plans to use posts 2m
apart. How many posts does he need
for each of the garden he could make?
DIFFICULT
12 gardens
12 posts

48. DIFFICULT

49. Read and Solve.
4. A floor of a library is shaped like a
parallelogram with the dimensions of
its side shown. It will be covered by
tiles with the same shape as the floor.
If the sides of the tiles are 1dm by ½
dm, how many tiles will be needed?
DIFFICULT
150 x 180 = 27 000 tiles

50. Read and Solve.
5. A chain of rectangles is formed when 1, 2, 3, … 50
squares are joined side by side. Each side of a
squares is 3cm long.
a. What is the perimeter of a square? a chain of 2
squares?
b. What is the perimeter of a chain of 3, 4 , 5
squares? Do you see a pattern?
c. What is the perimeter of a chain of 50 squares ?
d. Can you find a formula to find the perimeter of
a rectangle formed by a square?
DIFFICULT
1 sq. = 12cm 2 sq. = 18cm
3 sq. = 24cm
102 x 3 = 306 cm
2(n+1) 3cm ---
n is the no. of squares