Geometry & mensuration 1

08/22/11 GEOMETRY & MENSURATION Concepts To be remembered The lines are parallel and a transversal cuts these lines. If Angle 1 = Ѳ , A ngle2 = [180 – Ѳ ] 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1

08/22/11 GEOMETRY & MENSURATION Concepts To be remembered Lines AB & CD are parallel. E is a point such that Ľ BAE = 45 0 and Ľ ECD = 30 0 . Find Ľ AEC Draw a line GF passing through E parallel to AB F G 45 0 30 0 Ľ AEG = 45 0 Ľ GED = 30 0 Ľ AEC = 75 0 A D B C E 45 0 30 0

08/22/11 GEOMETRY & MENSURATION Concepts To be remembered Lines AB & CD are parallel. AE and CE are internal angular bisectors . Find Ľ AEC Let ĽFAB = 2x 0 Ľ ACD = 2x 0 . Ľ BAC = 2y 0 2x+2y = 180 0 Ľ CAE = y 0 Ľ ACE = x 0 X + Y = 90 From ∆ AEC, Ľ AEC = 90 0 2x A D B C E F y y x x

What is the sum of all internal angles in the figure? There are 8 triangles and hence the sum of all internal angles is 1440. 08/22/11 GEOMETRY & MENSURATION Concepts To be remembered What is the Sum Of all internal angles in Figure A,B,C & D? A = 720 B = 540 C = 360 D = 900 A B C D A J I H G F E D C B 1 6 7 8 5 4 3 2 1 4 3 2 1 3 2 1 2 1 5 4 3 2

08/22/11 Sum of all internal angles = (n-2) π Sum of all External angles = 2 π In a regular n sided figure, Each internal angle = (n-2) π /n Each external angle = 2 π /n GEOMETRY & MENSURATION N Sum of all internal Angles Average 3 180 60 4 360 90 5 540 108 6 720 120 7 900 900/7 8 1080 135 9 1260 140 10 1440 144

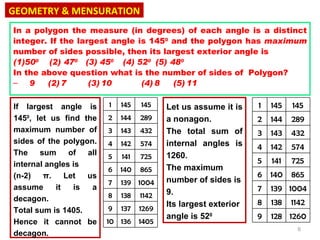
In a polygon the measure (in degrees) of each angle is a distinct integer. If the largest angle is 145 0 and the polygon has maximum number of sides possible, then its largest exterior angle is (1)50 0 (2) 47 0 (3) 45 0 (4) 52 0 (5) 48 0 In the above question what is the number of sides of Polygon? 9 (2) 7 (3) 10 (4) 8 (5) 11 GEOMETRY & MENSURATION If largest angle is 145 0 , let us find the maximum number of sides of the polygon. The sum of all internal angles is (n-2) π . Let us assume it is a decagon. Total sum is 1405. Hence it cannot be decagon. Let us assume it is a nonagon. The total sum of internal angles is 1260. The maximum number of sides is 9. Its largest exterior angle is 52 0 1 145 145 2 144 289 3 143 432 4 142 574 5 141 725 6 140 865 7 139 1004 8 138 1142 9 137 1269 10 136 1405 1 145 145 2 144 289 3 143 432 4 142 574 5 141 725 6 140 865 7 139 1004 8 138 1142 9 128 1260

The internal angles of a convex polygon are in arithmetic Progression. The smallest angle measures 50 0 and the common difference is 10 0 . The polygon has maximum number of sides “n”. n= 1) 3 2) 24 3) 3 0r 24 4) none of these. 08/22/11 Sn = n / 2 {100+10 (n-1)} =(n-2)180 50n+5n(n-1) = 180(n-2) 10n+n(n-1) = 36(n-2) n 2 +9n = 36n -72 n 2 - 27n+72 = 0 n = 3 Or 24 Answer : 3 Why? GEOMETRY & MENSURATION

The internal angles of a polygon are in arithmetic Progression. The smallest angle measures 65 0 and the common difference is 18¾ 0 . The number of sides of the polygon is 1) 8 2) 9 3) 10 4) 7 5) 11 08/22/11 Sn = = As the value on the right hand side is an integer, n or (n-1) should be divisible by 8. Hence substituting n= 9 , we get 1260 as the sum of all internal angles of a 9 sided figure. GEOMETRY & MENSURATION = (n-2)180 = (n-2)180 n 2 [ 130 + 75 4 (n -1) ] [ 65 n + 75 8 n(n -1) ]

For the side ED there can be only one triangle. For each side there will be only one triangle. Totally there are 5 such triangles 08/22/11 In a Pentagon how many triangles , using the vertices of Pentagon, can be formed such that only one side of the triangle is same as one side of the Pentagon. GEOMETRY & MENSURATION

In a Hexagon how many triangles , using the vertices of Hexagon, can be formed such that only one side of the triangle is same as one side of the hexagon. For the side ED there can be 2 triangles. For each side there will be 2 triangles. Totally there are 12 such triangles 08/22/11 GEOMETRY & MENSURATION In a Heptagon how many triangles , using the vertices of Heptagon, can be formed such that only one side of the triangle is same as one side of the Heptagon. For side ED there can be 3 triangles. For each side there will be 3 triangles. Totally there are 21 such triangles A B F C E D A B F C E D G

In a Decagon how many triangles , using the vertices of a Decagon can be formed such that only one side of the triangle is same as one side of the Decagon. For the side AB there can be 6 triangles. For each side there will be 6 triangles. Totally there are 60 triangles. 08/22/11 In a n sided figure ,how many triangles, using the vertices of the n sided figure, can be formed such that only one side of the triangle is same as one side of the n sided figure. For each side there will be (n – 4 ) triangles. Totally there will be n ( n – 4) triangles. GEOMETRY & MENSURATION A B

In a Pentagon how many triangles , using the vertices of Pentagon, can be formed such that two sides of the triangle are same as two sides of the Pentagon. There are 5 such triangles. 08/22/11 GEOMETRY & MENSURATION In a hexagon how many triangles , using the vertices of hexagon, can be formed such that two sides of the triangle are same as two sides of the hexagon. There are 6 such triangles. 08/22/11 A B C D E A B C D E F

In a heptagon how many triangles , using the vertices of heptagon, can be formed such that two sides of the triangle are same as two sides of the heptagon. There are 7 such triangles. 08/22/11 GEOMETRY & MENSURATION In a Decagon, how many triangles , using the vertices of Decagon, can be formed such that two sides of the triangle are same as two sides of the Decagon. There are 10 such triangles. In a n sided figure, how many triangles , using the vertices of n sided figure, can be formed such that two sides of the triangle are same as two sides of the n sided figure. There are n such triangles.

In a n sided figure, Let “x” represent the no. of triangles that can be formed, using the vertices of n sided figure, such that two sides of the triangle are same as two sides of the n sided figure. Let “Y” represent the no. of triangles that can be formed, using the vertices of n sided figure, such that only one side of the triangle is same as one side of the n sided figure. If x + y = 28. What is the value of n? X + Y = n + n(n-4) = 28 n 2 – 3n – 28 =0 (n – 7) (n +4) = 0 n = 7 08/22/11 GEOMETRY & MENSURATION

08/22/11 GEOMETRY & MENSURATION Certain Basic Notations & Facts. BC = a , CA = b & AB = c a + b > c b + c > a c + a > b ABC is called a right angled ∆ , if either Ĺ A or Ĺ B or Ĺ C equals 90 0 . b 2 = a 2 + c 2 ABC is called an acute angled ∆ , if Ĺ A , Ĺ B & Ĺ C are less than 90 0 . a 2 < b 2 + c 2 b 2 < c 2 + a 2 c 2 < a 2 + b 2 ABC is called an obtuse angled ▲ , if either Ĺ A or Ĺ B or Ĺ C is more than 90 0 . a 2 > b 2 + c 2 or b 2 > c 2 + a 2 or c 2 > a 2 + b 2 C A B a b c a b c C A B a b c C A B C A B c b a

08/22/11 GEOMETRY & MENSURATION How many obtuse angled ∆ can be drawn if two of the sides are 8 & 15 respectively. Let the third side be “x”. 8 ≤ x ≤ 22. Case 1: 15 is not the longest side x 2 > 8 2 +15 2 > 289 :: x 2 > 289 x > 17 :: x < 23 X can take values 18,19,20,21,22– 5 values. Case 2 : 15 is the longest side 225 > 8 2 + x 2 x 2 < 161 x < 13 x > 7 X can take values 8,9,10,11& 12 – 5 values Totally 10 triangles can be drawn. C A B 8 15 C A B 8 15

08/22/11 GEOMETRY & MENSURATION How many obtuse angled ∆les can be drawn if two of the sides are 6 & 10 respectively. Let “X” be the third side. 5 ≤ x ≤ 15. Case 1: 10 is the longest side 100 > 6 2 + x 2 x 2 < 64 x < 8 x > 4 X can take values 5,6 & 7 – 3 values Case 2: 10 is not the longest side x 2 > 6 2 +10 2 > 136 x > 11 x < 16 X can take values 12,13,14&15 – 4 values. Totally 7 triangles can be drawn. C A B 6 10 C A B 6 10

08/22/11 GEOMETRY & MENSURATION ∆ ABC & ∆ DEF are similar as Ĺ A = Ĺ D :: Ĺ B = Ĺ E :: ĹC = Ĺ F Then AB / DE = BC / EF = CA / FD ∆ ABC & ∆ DEF are similar as AB / DE = BC / EF = CA / FD = ¾ Then Ĺ A = Ĺ D :: Ĺ B = Ĺ E :: ĹC = Ĺ F C A B ǿ δ θ F D E ǿ δ θ C A B 6 8 12 F D E 3 4 6

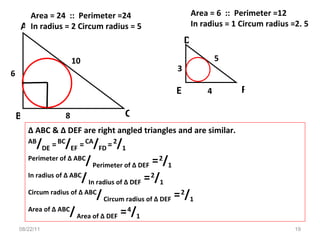
08/22/11 ∆ ABC & ∆ DEF are right angled triangles and are similar. AB / DE = BC / EF = CA / FD = 2 / 1 Perimeter of ∆ ABC / Perimeter of ∆ DEF = 2 / 1 In radius of ∆ ABC / In radius of ∆ DEF = 2 / 1 Circum radius of ∆ ABC / Circum radius of ∆ DEF = 2 / 1 Area of ∆ ABC / Area of ∆ DEF = 4 / 1 Area = 24 :: Perimeter =24 In radius = 2 Circum radius = 5 Area = 6 :: Perimeter =12 In radius = 1 Circum radius =2. 5 F D E C A B 3 4 5 6 8 10

08/22/11 GEOMETRY & MENSURATION ∆ ABC & ∆ DEF are similar as Ĺ A = Ĺ D :: Ĺ B = Ĺ E :: ĹC = Ĺ F AB / DE = BC / EF = CA / FD = m / n Perimeter of ∆ ABC / Perimeter of ∆ DEF = m / n In radius of ∆ ABC / In radius of ∆ DEF = m / n Circum radius of ∆ ABC / Circum radius of ∆ DEF = m / n Area of ∆ ABC / Area of ∆ DEF = m 2 / n2 C A B ǿ δ θ F D E ǿ δ θ

08/22/11 GEOMETRY & MENSURATION ABC &  EFD are similar. AB = 12 , EF = 8 . If BC = 18 , Find DF. ABC and  EFD are similar. AB / EF = AC / DE = BC / DF 12 / 8 = 18 / DF DF = 18*8 / 12 DF = 12 ABC and  ADE are similar and  ADE = area of quadrilateral DECB implies  ADE /  ABC = ½ AD / AB = √1 / √2. AD = 6√2 DB = AB - AD = 12 - 6√2 = 6 (2 - √2). In  ABC, let D & E be points on AB & AC such that  ABC and  ADE are similar and  ADE = area of quadrilateral DECB. If AB = 12 , Find DB. C A B ǿ δ θ F D E ǿ δ θ E C A B D ǿ δ θ δ θ

08/22/11 GEOMETRY & MENSURATION ▲ ABD = ⅟ 2 (BD) (Alt. from A to BC) ▲ ADC =⅟ 2 (DC) (Alt. from A to BC) ▲ ABD / ▲ADC = BD / DC = m / n If the base is divided in the ratio m : n, area of the 2▲ les so formed are in the ratio m : n. 1600 If area of triangle ABC is 100 sq units, what is the area of triangle ADE given that BD = 3 AB & CE =4 AC? Let us join DC. Consider ▲ ACD. AB:BD:: 1 : 3 ▲ BCD = 300 sq units ▲ ACD = 400 sq units Consider ▲ CDE. AC : CE :: 1 : 4 ▲ CDE= 1600 Sq.units ▲ ADE=2000 Sq.units A B C D m n A B C D E 3 100 1 300 4 1

08/22/11 GEOMETRY & MENSURATION If area of triangle ABC is 20 sq units, what is the area of triangle ADE given that BD = 9 AB & CE =19AC? Let us join DC. Consider ∆ACD. AB:BD::1:9 ∆ BCD= 180 sq units. ∆ACD =200 sq units AC: CE:: 1:19 ∆ CDE= 3800 Sq.units ∆ ADE=4000 Sq.units If area of triangle ABC is “x” sq units, what is the area of triangle ADE given that BD = k AB & CE =m AC? Let us join DC. Consider ∆ACD. AB:BD::1:k ∆ BCD = k x sq units ∆ ACD = x + kx sq units AC: CE:: 1:m ∆ CDE= m(x+kx )Sq.units ∆ ADE=(k+1)(m+1)x 180 9 20 1 A B C D E 19 1 3800 A B C D E 1 1 K m x kx m(x+kx)

In a  ABC, AD is median from A to BC.  ABD =  ADC (Why?) BE is median from B to CA. CF is median from C to AB The point of concurrence is Centroid (G) Centroid divides the median in the ratio 2:1  AGF =  BGF =  BGD CGD =  CGE =  AGE = X AB 2 +AC 2 =2(AD 2 +BD 2 ) BA 2 +BC 2 =2(BE 2 +CE 2 ) CA 2 +CB 2 =2(CF 2 +AF 2 ) A B C E G F D GEOMETRY & MENSURATION 08/22/11

GEOMETRY & MENSURATION 08/22/11 AB 2 + AC 2 = 2(AD 2 +BD 2 ) 16 2 + 8 2 = 2(AD 2 +6 2 ) AD 2 = 124 In ∆ ABC, AB = 16,BC= 12, AC = 8. Find AD, BE & CF (Medians) BC 2 + BA 2 = 2(BE 2 +CE 2 ) 16 2 + 12 2 = 2(BE 2 +4 2 ) BE 2 = 184 CB 2 + CA 2 = 2(CF 2 +BF 2 ) 12 2 + 8 2 = 2(BE 2 +8 2 ) CF 2 = 40 BE > AD > CF BE 2 + AD 2 + CF 2 = 348 AB 2 + BC 2 + CA 2 = 464 [ BE 2 + AD 2 + CF 2 ] /[ AB 2 + BC 2 + CA 2 ] = ¾ D G A B E F C

GEOMETRY & MENSURATION 08/22/11 AD 2 = 6 2 + 4 2 = 52 CF 2 = 8 2 + 3 2 = 73 BE 2 = 25 In a right angled  ABC, AB = 6 BC = 8 & AC = 10. Let AD , BE & CF be medians. CF > AD > BE BE 2 + AD 2 + CF 2 = 150 AB 2 + BC 2 + CA 2 =200 [ BE 2 + AD 2 + CF 2 ] / [ AB 2 + BC 2 + CA 2 ] = ¾ D G A B E F C

08/22/11 BC = 10 ABC . CA = 26.The given triangle is divided into 2 triangles whose areas are equal. What is the maximum possible sum of perimeter of the 2 triangles so formed? The given triangle can be divided into 2 triangles whose areas are equal if we draw a median . As maximum perimeter of the 2 triangles so formed is sought, the longest median is to be drawn. Longest Median is to the shortest side. AF = √601. Maximum possible perimeter of the 2 triangles so formed is 60+2 √601 A C B GEOMETRY & MENSURATION 5 5 F 24 √ 601

In the triangle given alongside, AD, BE & CF are medians. GECD is a cyclic quadrilateral, find the ratio of AE:GD. GECD is a cyclic quadrilateral implies that the vertices G, E, C & D lie on a circle. Therefore AG * AD = AE * AC If GD = Y AG = 2Y & AD = 3Y If AE = X ,EC = X , AC = 2X X * 2 X = 2Y *3 Y X= √3 Y. The ratio is √3 : 1 08/22/11 A B C E G F D GEOMETRY & MENSURATION

In the triangle given alongside, D,E & F are midpoints of sides BC, CA & AB. AK is ┴ r from A to BC. Find ĹFKD +Ĺ FED. 08/22/11 A B K D F E C X X X X GEOMETRY & MENSURATION Consider ∆AFE & ∆ ABC L AFE = L ABC = X Consider ∆CED & ∆ ABC L FED = L AFE = X Consider ∆ABK, FK is median to Hyp AB. Hence FK = FB. Hence L FKB = X L FKD = (180 -X) L FED + L FKD = 180

Medians – Points to remember A median divides a triangle into 2 triangles whose areas are equal Three medians divide the triangle into 6 triangles whose areas are equal. The point of concurrence is called centroid. Centroid divides the median in the ratio 2:1 AB 2 +AC 2 =2(AD 2 +BD 2 ) BA 2 +BC 2 =2(BE 2 +CE 2 ) CA 2 +CB 2 =2(AF 2 +BF 2 ) where AD,BE & CF are Medians Median to hypotenuse in a right angled  is half the hypotenuse. Shortest median is to the longest side. Longest Median is to the shortest side. Ratio of Sum of squares of medians to sum of squares of sides is 3:4 08/22/11

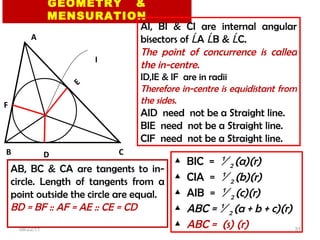
GEOMETRY & MENSURATION 08/22/11 A B C I D E F AI, BI & CI are internal angular bisectors of Ĺ A Ĺ B & Ĺ C. The point of concurrence is called the in-centre. ID,IE & IF are in radii Therefore in-centre is equidistant from the sides. AID need not be a Straight line. BIE need not be a Straight line. CIF need not be a Straight line. AB, BC & CA are tangents to in-circle. Length of tangents from a point outside the circle are equal. BD = BF :: AF = AE :: CE = CD ▲ BIC = ⅟ 2 (a)(r) ▲ CIA = ⅟ 2 (b)(r) ▲ AIB = ⅟ 2 (c)(r) ▲ ABC = ⅟ 2 (a + b + c)(r) ▲ ABC = (s) (r)

GEOMETRY & MENSURATION 08/22/11 A B C I D BI & CI are internal angular bisectors of Ĺ B & Ĺ C respectively. I is the in-centre & L BAC = 70 0 , find the angle BIC. Consider ∆ ABC, 2X+2Y = 110 X+Y = 55 Consider ∆ BIC, Ø+X+Y = 180 Ø = 125 0 :: Ø = 90+ ½ Ĺ A 70 ø AI, BI & CI are internal angular bisectors of Ĺ A Ĺ B & Ĺ C. ĹBIC = 90+ ⅟ 2 A ĹCIA = 90+ ⅟ 2 B ĹAIB = 90+ ⅟ 2 C X Y X Y

GEOMETRY & MENSURATION 08/22/11 A B C I D E F AI, BI & CI are internal angular bisectors of Ĺ A Ĺ B & Ĺ C. ID,IE & IF are in radii. If AB=20, AC=22 &BC= 24. Find BD. AB=20 AC=22 BC= 24. Let BD = X :: BF = X AF =AB – BF = 20 – X AE = 20 – X CE = AC – CE = X + 2 CD= X+2 BD+CD = 2X+2 = 24 2X = 22 X =11 BD = BF = [BC + BA – AC] / 2 CD = CE = [CB + CA – AB] / 2 AF = AE = [AB + AC – BC] / 2 X X 20 - x 20 - x 2+ x 2+ x

In the given AB = 6, BC = 8 & AC = 10 and angle B is 90 0 . Find radius of the circle inscribed in the Triangle. Area of Triangle ABC = ⅟ 2 (6)(8) = 24 sq. units Semi perimeter = 12 units Area of Triangle ABC = (12)(r) = 24 sq. units :: r= 2 2r+4 = 8 implies r = 2 units 08/22/11 GEOMETRY & MENSURATION In a  ABC, AB = 17, BC = 25, CA = 28, find in-radius S = [17 + 25 + 28] / 2 = 35  35*18*10*7 = 35*r 35*18*10*7=35 2 * r 2 r 2 = 36. r = 6 o B A C r r r r 6-r 6-r r+4 r+4 B A C

ABCD is a square. E is the midpoint of BC. Find the ratio of in-radius of the circle inscribed in the ∆ DCE, to the side of the square. AB = BC = CA=DA = 2a In radius of circle = “r”. Consider ∆ DCE. CE = a ::CD = 2a :: DE = √5 a “ s” = (3+ √5 ) a / 2 ∆ DCE = ½ (2a)(a) ∆ DCE = ½ (3+√5)a r r / 2a = 1 / (3+√5) 2a A B √ 5 a E c D 2a 08/22/11 a r GEOMETRY & MENSURATION

∆ ABC,AB=16,BC=18 &AC = 20. If AD is an internal angular bisector, Find BD ∆ ABC, AB=16, BC=18 AC=20. Let CE be parallel to AD ∆ ABD III r ∆ EBC BD / DC = AB / AC = 16 / 20 BD = 4K CD = 5K BD = 4K = 8 ∆ ABC, internal angular bisector divides the BC in the ratio in the ratio of sides. BD / DC = AB / AC 08/22/11 A B C ø ø ø ø E D GEOMETRY & MENSURATION

08/22/11 E B C D A Given ABC is any triangle.AD is external angular bisector of L EAC. BD is internal angular bisector of L ABC. What is the value of L ADB - ½L ACB? Let L ABC = 2X L ACB = 2Y L BAC = 2Z. 2x+2y+2z = 180 L EAC = 2X+2Y L DAC = X+Y. From ∆ ADB, ǿ+x+2z+x+y = 180 ǿ - y = 0 L ADB - ½L ACB = 0 x x 2z 2y x + y x + y ǿ GEOMETRY & MENSURATION

ABC is a right angled triangle L B = 90 0. AB = 24. BC = 7. AD is external angular bisector, D is a point on BC Extended. Find CD. Let AD be the external angular bisector. Draw BE ║ l to AD LAEB = LABE = X AE = AB = 24 EC = 1 ∆ CEB ||| r ∆ CAD CE /EA = CB/BD BD = 168 CD = 175 08/22/11 7 168 1 24 24 A B c D E GEOMETRY & MENSURATION X X X X

ABC is a right angled triangle L B = 90 0. AB = 15. BC = 8. AD is external angular bisector, D is a point on BC Extended. Find CD. Let AD be the external angular bisector. Draw BE parallel to AD LAEB = LABE = X AE = AB = 15 EC = 2 ∆ CEB ||| r ∆ CAD CE /EA = CB/BD BD = 60 CD = 68 08/22/11 8 60 2 15 15 A B c D E GEOMETRY & MENSURATION X X X X

GEOMETRY & MENSURATION 08/22/11 y xy/(z-x) z -x x x A B c D E ABC is a right angled triangle L B = 90 0. AB = x. BC = y. AD is external angular bisector, D is a point on BC Extended. Find CD. Let AD be the external angular bisector. Draw BE parallel to AD LAEB = LABE = x AE = AB = x EC = z -x ∆ CEB ||| r ∆ CAD CE /EA = CB/BD BD = x y / (z-x) ø ø ø ø

ABC is a right angled triangle L B = 90 0. AB = 8. BC = 6. AD is external angular bisector, D is a point on BC Extended. Find AD. Let AD be the external angular bisector. Draw BE parallel to AD LAEB = LABE = X AE = AB = 8 EC = 2 ∆ CEB ||| r ∆ CAD CE /EA = CB/BD BD = 24 AD = √640 08/22/11 6 24 2 8 8 A B c D X E GEOMETRY & MENSURATION √ 640 X X X

Area of ∆ ABC Let AD be the altitude from A to BC. Sin C= AD/AC = AD/b AD = b Sin C Area of ∆ ABC = ½ (BC) (AD) = ½ (a) (AD) = ½ a b Sin C 08/22/11 A B C D ┐ GEOMETRY & MENSURATION ABC is a triangle with AB = 7 & AC = 5. Given L BAD= L CAD = 60 0. Find AD. ∆ ABD = ½ (7) (AD) Sin 60 ∆ ADC = ½ (5) (AD) Sin 60 ∆ ABC = ½ (7) (5) Sin 120 ∆ ABC = ∆ ABD+ ∆ ADC = ½{7(AD)Sin60+5(AD)Sin60} = ½ (7) (5) Sin 120 AD = 35/12 A B D C 5 7 60 60

ABC is a triangle with AB = α & AC = β . Given L BAD= L CAD = X 0. Find AD. ∆ ABD = ½ ( α ) (AD) Sin 60 ∆ ADC = ½ ( β ) (AD) Sin 60 ∆ ABC = ½ ( α ) ( β ) Sin 120 ∆ AB C = ∆ ABD+ ∆ ADC = ½{ α (AD)Sin x+ β (AD)Sin x } = ½ ( α ) ( β ) Sin 2x AD = α β Sin 2x / [ α + β ] Sin x 08/22/11 A B C D β α x x GEOMETRY & MENSURATION

GEOMETRY & MENSURATION 08/22/11 A B C I D E F AI, BI & CI are internal angular bisectors of Ĺ A Ĺ B & Ĺ C. ID,IE & IF are in radii. If BF=6, CE=8 and ID = 4. Find AB+AC. ∆ ABC = √s(s-a)(s-b)(s-c) ∆ ABC = √(14+x)(x)(8)(6) ∆ ABC = “s” “r” s = 14+x ∆ ABC = (14+x) (4) (14+x)(x)(8)(6) = (14+x) 2 (16) 48x = (14+x) (16) 3x = (14+x) 2x = 14 :: x = 7 AB+AC = 28 6 8 6 8 x x

In a  ABC, AD is altitude from A to BC. BE is altitude from B to CA. CF is altitude from C to AB The point of concurrence is orthocentre (H) AFHE is a cyclic quadrilateral DHEC is a cyclic quadrilateral DHFB is a cyclic quadrilateral Geometry & Mensuration A B C E H F D If ĹFAE = 70 o , what is Ĺ BHC? FHEA is a Cyclic Quadrilateral. ĹFAE = 70 o ĹFHE = 110 o ĹBHC = 110 o 08/22/11

In a triangle ABC, one of the side is 10 units .The longest side is 20 units. Area is 80 sq units.Find the third side. Geometry & Mensuration A B C D Let AD be the altitude  ABC = ½ (20) (AD) = 80 AD = 8 units From  ABD, BD 2 = AB 2 – AD 2 = 10 2 – 8 2 = 36 = 6 DC = 14 From  ADC , AC2 = AD 2 + DC 2 = 8 2 + 14 2 = 260 AC = √260 14 8 10 6 √ 260 08/22/11

In a triangle ABC, one of the sides is 10 units & another side is 20 units. Area is 80 sq units. Find the longest side. Geometry & Mensuration A B C D Let AD be the altitude  ABC = ½ (20) (AD) = 80 AD = 8 units  ADB, DB 2 = AB 2 – AD 2 = 10 2 – 8 2 = 36 DB = 6 :: DC = 26  ADC , AC 2 = AD 2 + DC 2 = 8 2 + 26 2 = 740 AC = √ 740 20 8 10 6 √ 740 08/22/11

In a  ABC, AB = AC = 100 units, the area of the triangle is not less than 4800 sq units. What is the difference between maximum and minimum perimeter of such a triangle? Geometry & Mensuration A B C D y x 100 y 100 Let AD be the altitude & AD = X. The altitude bisects the base in an isosceles triangle. Let BC = 2Y x = √ 100 2 – y 2 ½ { (2y) (x) } ≥ 4800 y {√100 2 – y 2 } ≥ (4800) y 2 (√ 100 2 – y 2 ) 2 ≥ (4800) 2 y 4 – 10000y 2 + (4800) 2 ≤ 0 (y 2 – 3600) (y 2 – 6400) ≤ 0 3600 ≤ y 2 ≤ 6400 :: 60 ≤ y ≤ 80 60 ≤ y ≤ 80 Min perimeter 320. Max perimeter 360 . Diff 40. 08/22/11

ABC is a right angled triangle. AB = 6 BC = 8 CA = 10 . BE is a median & BD is ┴ r from B to AC. Find DE. Let BD & BE be altitude & Median respectively. BE =5.0 ½(6)(8) = ½(10)(BD) BD = 4.8 units DE=√{(5.0) 2 - (4.8) 2 } = √1.96 = 1.4 08/22/11 A B C 10 8 6 D E 5 4.8 Geometry & Mensuration ABC is a right angled triangle. ĹB = 90. BD is ┴ r from B to AC. AE = 4 EC = 9 . Find BE. Consider ∆ AEB & ∆ BEC. Ĺ AEB = 90 = Ĺ BEC Ĺ ABE = ø = Ĺ ECB. The other angle must be equal ∆ AEB ||| r ∆ BEC. BE / AE = EC / BE. BE 2 = (AE) (EC)=4*9 :: BE = 6 ø ø A B C 9 4 E

ABC is a right angled triangle. Ĺ B = 90. BE is ┴ r from B to AC. Consider ∆ AEB & ∆ BEC. Ĺ AEB = 90 = Ĺ BEC. Ĺ ABE = ø = Ĺ ECB. The other angle must be equal ∆ AEB ||| r ∆ BEC. BE / AE = EC / BE :: BE 2 = (AE) (EC) ABC is a right angled triangle. Ĺ B = 90. BE is ┴ r from B to AC. Consider ∆ AEB & ∆ ABC. Ĺ AEB = 90 = Ĺ BEC. Ĺ ABE = ø = Ĺ ACB. The other angle must be equal ∆ AEB ||| r ∆ ABC. AE / AB = AB / AC = BE / BC ABC is a right angled triangle. Ĺ B = 90. BE is ┴ r from B to AC. Consider ∆ CEB & ∆ ABC. Ĺ CEB = 90 = Ĺ ABC. Ĺ CBE = ø = ĹC AB. The other angle must be equal ∆ AEB ||| r ∆ ABC. BE / AB = BC / AC = CE / BC 08/22/11 A B C E ┐ ┘ Geometry & Mensuration ø ø

ABC is a right angled triangle. Ĺ B = 90. BE is ┴ r from B to AC. We get 3 sets of similar triangles. ∆ ∆ AEB ||| r ∆ BEC ∆ AEB ||| r ∆ ABC ∆ BEC ||| r ∆ ABC 08/22/11 A B C E ┐ ┘ Geometry & Mensuration ø ø In  ABC, D, E & F are midpoints of BC, CA & AB. Let L 1 , L 2 , L 3 represent ┴r passing through D, E, F.L 1 , L 2 , L 3 are ┴r bisectors of BC, CA & AB.The point of concurrence is “s”, circumcentre SA – SB = SC Circumcentre is equidistant from vertices A B F D C E S

Area of  ABC = ½ (b) (c) Sin A. Let BD be the diameter of the circum circle Then L A = L D and BD = 2R,where R is the circum radius. From  BDC, Sin D = a / 2R = Sin A Area of  ABC = abc / 4R Geometry & Mensuration a c b Area of  ABC = ½ (b) (c) Sin A. Let BD be the diameter of the circum circle Then L A = L D and BD = 2R,where R is the circum radius. From  BDC, Sin D = a / 2R = Sin A Similarly a / SinA = b / SinB = c / SinC = 2R 08/22/11 A B D C S A B D C S

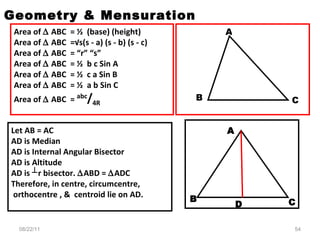
Area of  ABC = ½ (base) (height) Area of  ABC =√s(s - a) (s - b) (s - c) Area of  ABC = “r” “s” Area of  ABC = ½ b c Sin A Area of  ABC = ½ c a Sin B Area of  ABC = ½ a b Sin C Area of  ABC = abc / 4R a / SinA = b / SinB = c / SinC = 2R COS A = [b 2 + c 2 - a 2 ] / 2bc COS B = [c 2 + a 2 - b 2 ] / 2ca COS C = [a 2 + b 2 - c 2 ] / 2ab Area of  ABC = ( √3 / 4 ) ( a 2 ) if  ABC is equilateral triangle of side “a”. Geometry & Mensuration 08/22/11 A B C b c a

Area of  ABC = ½ (base) (height) Area of  ABC =√s(s - a) (s - b) (s - c) Area of  ABC = “r” “s” Area of  ABC = ½ b c Sin A Area of  ABC = ½ c a Sin B Area of  ABC = ½ a b Sin C Area of  ABC = abc / 4R Geometry & Mensuration Let AB = AC AD is Median AD is Internal Angular Bisector AD is Altitude AD is ┴r bisector.  ABD =  ADC Therefore, in centre, circumcentre, orthocentre , & centroid lie on AD. A B C 08/22/11 A B D C

Geometry & Mensuration Let ABC be a right angled triangle ĹABC = 90 . AD is Median. BE is Median. AE = EC. B is orthocentre.E is circumcentre Centroid lies on BE.G is Centroid. BG/GE = 2/1. In any triangle, Centroid divides the line joining Orthocentre and circumcentre in the ratio 2:1 . The proof is indicative . Let ABC be an Equilateral triangle. AD, BE & CF are Medians, Altitudes ,┴r bisectors, & internal angular bisectors . G is Centroid ,incentre , Circumcentre and Orthocentre Let AB = AC . AD is Median . AD is Internal Angular Bisector . AD is Altitude AD is ┴r bisector.  ABD =  ADC Therefore, in centre, circumcentre, orthocentre , & centroid lie on AD. 08/22/11 A B G C D E A B F E D C G A B D C

Geometry & mensuration 1

More Related Content

What's hot

Similar to Geometry & mensuration 1

Recently uploaded

Geometry & mensuration 1