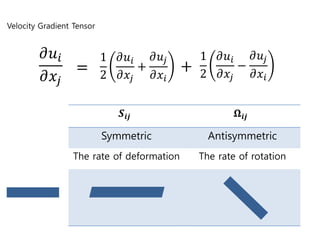
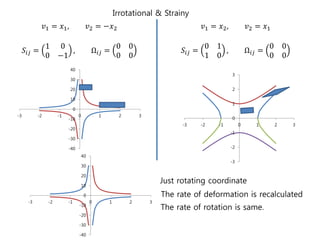
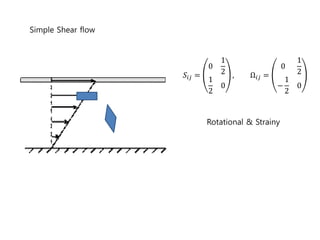
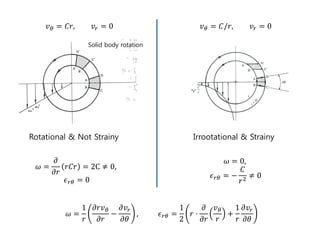
1) The velocity gradient tensor decomposes the rate of deformation tensor (Sij) and the rate of rotation tensor (Ωij). Sij is symmetric and represents straining motions while Ωij is antisymmetric and represents rotational motions. 2) Simple examples are analyzed to demonstrate irrotational and rotational flows, and how the tensors decompose them into straining and rotational parts. 3) Solid body rotation is shown to be purely rotational without strain, while other examples like plane shear flow contain both straining and rotational motions.

1. Class Review (3/13)
Jong su, Kim

2. Velocity Gradient Tensor
𝜕𝑢 𝑖 1 𝜕𝑢 𝑖 𝜕𝑢 𝑗 1 𝜕𝑢 𝑖 𝜕𝑢 𝑗
= + + 2 𝜕𝑥 𝑗
−
𝜕𝑥 𝑖
𝜕𝑥 𝑗 2 𝜕𝑥 𝑗 𝜕𝑥 𝑖
𝑺 𝒊𝒋 𝛀 𝒊𝒋
Symmetric Antisymmetric
The rate of deformation The rate of rotation

3. 𝑺 𝒊𝒋 𝛀 𝒊𝒋
𝑛 𝑠 𝑠 Connected with dual vector
𝑠 𝑛 𝑠 𝐴
1 𝜕𝑣 𝑘
𝑠 𝑠 𝑛 def. Ω 𝑗𝑖 = 2 𝜖 𝑖𝑗𝑘 𝑤 𝑘 , 𝑤 𝑖 = 𝜖 𝑖𝑗𝑘
𝜕𝑥 𝑗
𝐴
𝜕𝑣 𝑘
s : Shear Strain 𝑤 𝑖 = 𝜖 𝑖𝑗𝑘 = 𝜖 𝑖𝑗𝑘 Ω 𝑗𝑘
𝜕𝑥 𝑗
n : Normal Strain
𝜖 𝑖𝑙𝑚 𝑤 𝑖 = 𝜖 𝑖𝑙𝑚 𝜖 𝑖𝑗𝑘 Ω 𝑗𝑘 = 𝛿 𝑖𝑗 𝛿 𝑚𝑘 − 𝛿 𝑙𝑘 𝛿 𝑚𝑗 Ωjk
= Ω 𝑙𝑚 − Ω 𝑚𝑙
= 2Ω 𝑙𝑚
1
Ω 𝑙𝑚 = 𝜖 𝑖𝑙𝑚 𝑤 𝑖
2

4. Irrotational & Strainy
𝑣1 = 𝑥1 , 𝑣2 = −𝑥2 𝑣1 = 𝑥2 , 𝑣2 = 𝑥1
1 0 0 0 0 1 0 0
𝑆 𝑖𝑗 = , Ω 𝑖𝑗 = 𝑆 𝑖𝑗 = , Ω 𝑖𝑗 =
0 −1 0 0 1 0 0 0
40
3
30
20 2
10
1
0
-3 -2 -1 0 1 2 3
-10 0
-3 -2 -1 0 1 2 3
-20
-1
-30
-40 -2
40
-3
30
20
10
Just rotating coordinate
0 The rate of deformation is recalculated
-3 -2 -1 0 1 2 3
-10
The rate of rotation is same.
-20
-30
-40

5. Simple Shear flow
1 1
0 0
𝑆 𝑖𝑗 = 2 , Ω 𝑖𝑗 = 2
1 1
0 − 0
2 2
Rotational & Strainy

6. 𝑣 𝜃 = 𝐶𝑟, 𝑣𝑟 = 0 𝑣 𝜃 = 𝐶/𝑟, 𝑣𝑟 = 0
Solid body rotation
Rotational & Not Strainy Irrootational & Strainy
𝜕 𝜔 = 0,
𝜔= 𝑟𝐶𝑟 = 2C ≠ 0, 𝐶
𝜕𝑟 𝜖 𝑟𝜃 =− 2≠0
𝜖 𝑟𝜃 = 0 𝑟
1 𝜕𝑟𝑣 𝜃 𝜕𝑣 𝑟 1 𝜕 𝑣𝜃 1 𝜕𝑣 𝑟
𝜔= − , 𝜖 𝑟𝜃 = 𝑟⋅ +
𝑟 𝜕𝑟 𝜕𝜃 2 𝜕𝑟 𝑟 𝑟 𝜕𝜃