This document discusses the improvement of interleaved methods for estimating ranking function outcomes using statistical hypothesis testing, particularly in scenarios with long-tailed query distributions. The paper reproduces and evaluates previous work on interleaved methods, proposing two variations for the δab score estimator: stat-pruning and stat-weight, to enhance evaluation accuracy. Experiments reveal the limitations and benefits of these methods across differing query distributions, highlighting challenges in reproducing original findings due to incomplete information.

1. ECIR 2023
05/04/2023
Alessandro Benedetti, Director @ Sease
Anna Ruggero, R&D Software Engineer @ Sease
Stat-Weight: Improving the Estimator
of Interleaved Methods Outcomes with
Statistical Hypothesis Testing

2. ONLINE EVALUATION
Online evaluation estimates the best ranking function for a
system, observing a live instance with real users and data.
Previous works have been evaluated
on a uniform distribution of
queries.
In real-world applications, the same
query is executed multiple times
by different users and in different
sessions, leading to a long tail
distribution.

3. 100%
Model A Model B
2
1 3 1 2 3
1 2 3 4
INTERLEAVING

4. OUTCOME ESTIMATOR
Outcome: which ranker is the best (A or B)
wins(A) = #queries where ranker A received more clicks than B
ties(A,B) = #queries where ranker A and B received the same number of clicks
wins(B) = #queries where ranker B received more clicks than A
> 0 winner A
< 0 winner B
= 0 tie

5. REPRODUCIBILITY PAPER
This paper aims to reproduce and then replicate:
Hofmann, Katja, Shimon Whiteson, and Maarten De Rijke
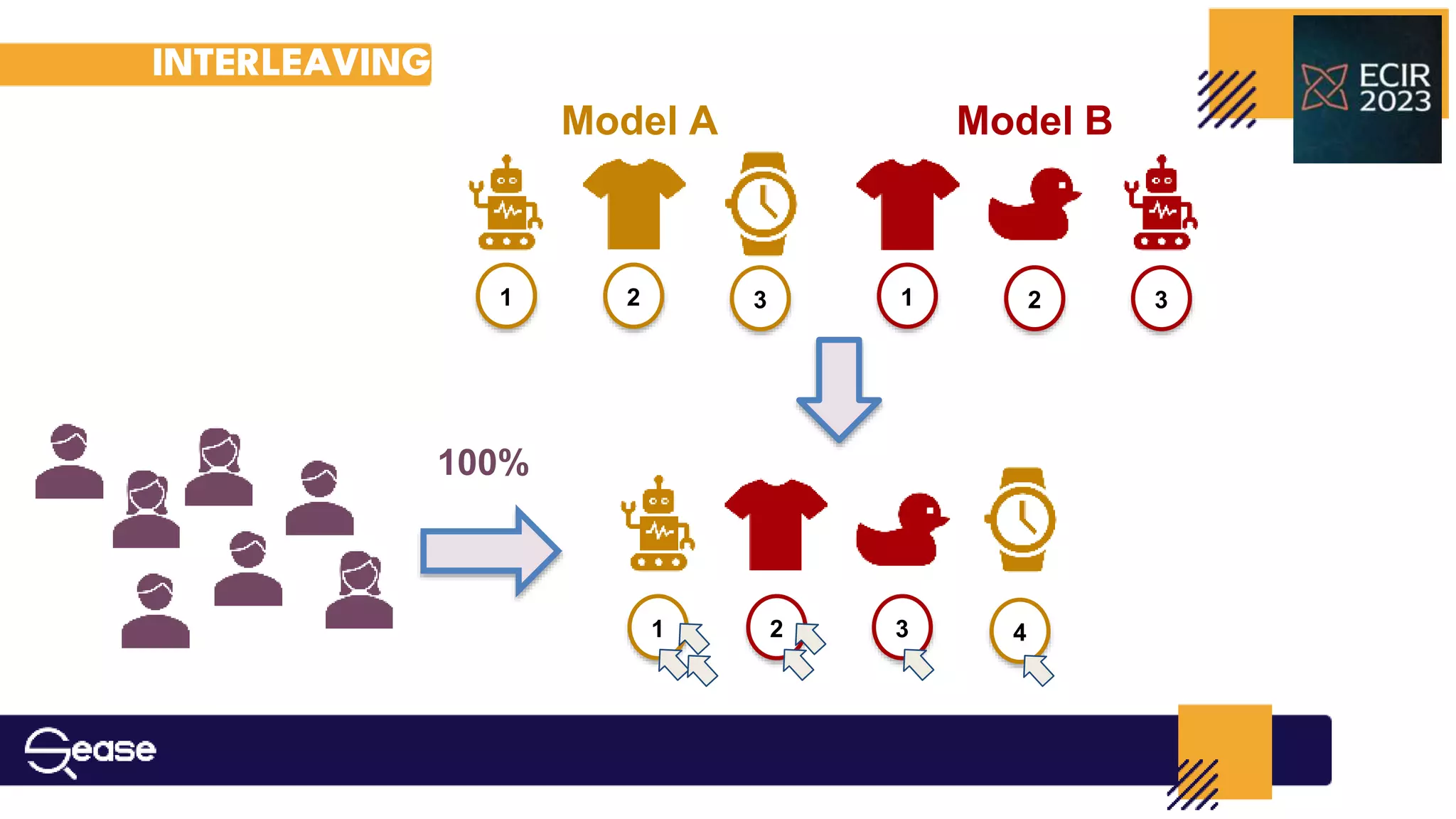
"A probabilistic method for inferring preferences from clicks." [¹]
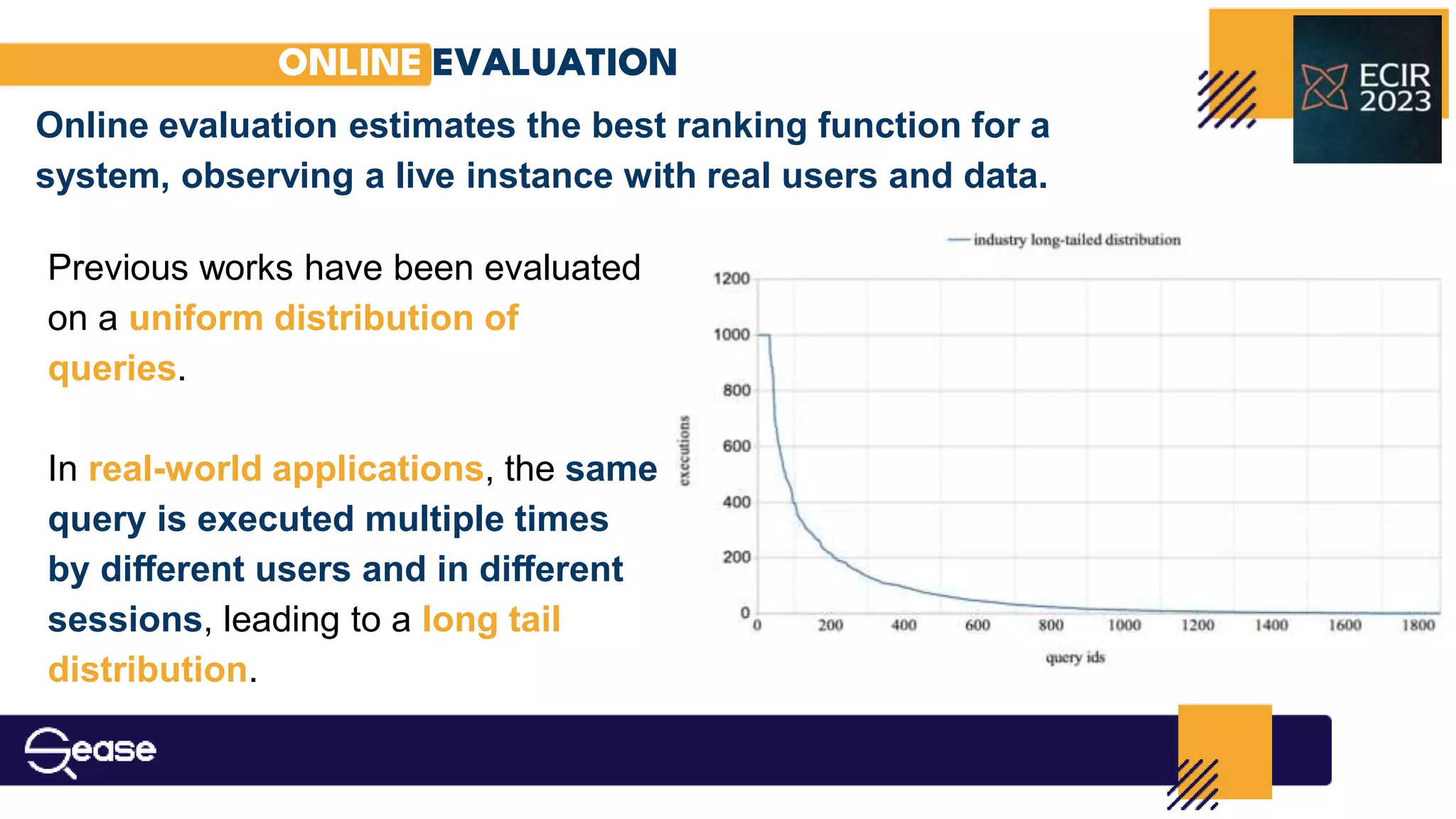
investigating the effect that different query distributions have on the
accuracy of interleaving.
Reason:
It is one of the most prominent surveys on interleaved methods and presents
an experimental setup that felt perfect to evaluate the long-tailed real-world
scenario.
[¹] https://dl.acm.org/doi/abs/10.1145/2063576.2063618

6. RESEARCH QUESTIONS
- RQ1: Is it possible to reproduce the original paper experiments?
- RQ2: How does the original work generalise in the real-world scenario where
queries have a long-tailed distribution?
- RQ3: Does applying statistical hypothesis testing improve the evaluation
accuracy in such a scenario?

7. OUR CONTRIBUTION
The ΔAB score estimator considers all queries equal (each win has credit 1)
This may include wins with
- few clicks: clicks A = 3 total clicks = 5 -> win(A)
- similar preferences: clicks A = 5001 total clicks = 10000 -> win(A)
To mitigate this problem, this paper proposes two variations for the ΔAB score:
stat-pruning and stat-weight.

8. Our null hypothesis:
the two ranking functions we are comparing are equivalent
i.e. the probability of each ranking function winning is 0.5
For each query:
- we observe the number of clicks collected
- we calculate a p-value, 0 < p-value < 0.5
- 0 = observed clicks are very unlikely to have happened by chance
- 0.5 = observed clicks are very likely to have happened by chance
STATISTICAL HYPOTHESIS TESTING

9. Total n° of clicks Clicks for winning ranker A P-value credit win A
5000 2501 0.01
4 3 0.38
5000 2600 0.99
STATISTICAL HYPOTHESIS TESTING

10. STAT - PRUNING
Simplest and most aggressive:
we keep
Significance level α = 0.05.
If the p-value is below the threshold, the result is considered significant.
The queries not reaching significance are discarded before the ΔAB score
calculation (credit = 0)

11. STAT - WEIGHT
The idea is to assign a different credit to each win and tie in the
original ΔAB score.
This credit is the estimated probability of the
win/tie to have not happened by chance:
the p-value is normalised with a min-max normalization
(min = 0 and max = 0.5) to be between 0 and 1

12. STAT - WEIGHT
The proposed updates to the ΔAB score formula are the following:
- qa is in the query set showing a
preference for the rankerA.
- qb is in the query set showing a
preference for the rankerB.
- qt belongs to the query set
showing a tie.

13. RESEARCH QUESTIONS
- RQ1: Is it possible to reproduce the original paper experiments?
- RQ2: How does the original work generalise in the real-world scenario where
queries have a long-tailed distribution?
- RQ3: Does applying statistical hypothesis testing improve the evaluation
accuracy in such a scenario?

14. EXPERIMENTS - SETUP
First set of experiments: we address RQ1 with the same settings and data as the
original work (uniform query distribution).
Second set of experiments: we address RQ2 and RQ3 introducing a long-tailed
query distribution.

15. DATASET
Dataset:
fold 1 from MSLR-WEB30k dataset: 18, 919 queries, with an average of 119.96
judged documents per query.
Each <query, document> pair is described by 136 features.
Long Tail Distribution: extracted from the query log of an e-commerce search
engine
Each query is associated with the number of times it was executed.
The amount of users collected per query is capped to 1000.
Fully anonymised

16. - Uniform query distribution
- Perfect click model
- 136 rankers =
9180 comparisons
- Long tail query distribution
- Perfect click model
- Long tail query distribution
- Realistic click model
- 136 rankers = 9180 comparisons
RESULTS

17. CHALLENGES
- Substantial amount of work and discussions with the original authors
required to try to figure out the exact parameters and code used in the
original runs
- Not possible to exactly reproduce the reported accuracy for TDI due to
missing information and code unavailability.

18. CONCLUSIONS
Stat-weight
● consistent across realistic uniform and long-tailed query distributions
● sensitive to small differences between the rankers
● robust to noise.
Stat-pruning
● doing well in long-tailed query distributions
● too aggressive
● hyper-parameter α that can be tricky to tune

19. THANK YOU!
@seaseltd @sease-
ltd
@seaseltd @sease_ltd