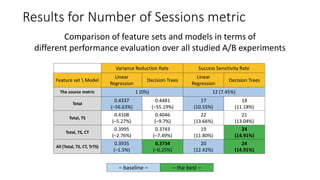
The document discusses using machine learning techniques to improve the sensitivity of A/B testing. It describes how A/B testing works by splitting users randomly into groups A and B that are exposed to different variants of a service. Key measures are calculated for each user and the groups are compared to determine if one variant is better. The document then discusses challenges with detecting small effects with limited user traffic. It proposes learning sensitive combinations of existing A/B testing metrics and predicting metrics to reduce variance as ways to improve sensitivity and the ability to detect smaller effects. Results show these machine learning approaches can increase sensitivity by detecting effects with less user data compared to traditional metrics.

1. Pavel Serdyukov
Machine learning
powered A/B
testing

2. A/B testing methodology

3. Group
A
Group
B
Split
them
randomly
trafficofusers
Variant for A
Variant for B
Expose to one of
two variants of the service
e.g., the current production version
e.g., an evaluated update
Calculate a key
measure for each user
X(uA1)
…
Calculate the OEC for each
group as the mean value
e.g., X(u) is the number
of sessions of the user u
X(uA2)
X(uA3)
X(uA4)
X(uA5)
X(uB1)
…
X(uB2)
X(uB3)
X(uB4)
X(uB5)
μA(X)=avgu in AX(u)
μB(X)=avgu in BX(u)
Overall Evaluation Criterion
(OEC) for the group B
Overall Evaluation Criterion
(OEC) for the group A

4. μA(X)=avgu in AX(u)
μB(X)=avgu in BX(u)
Overall Evaluation Criterion
(OEC) for the group B
Overall Evaluation Criterion
(OEC) for the group A
Calculate the OEC for each
group as the mean value
Δ(x) VS 0
Δ(X) = μB(X) – μA(X)
the evaluated update is
positive or negative
Statistical
significance test
the difference is caused
by a noise or
the treatment effect
(e.g., Student’s t-test)
Overall Evaluation
Criterion (OEC)
[Kohavi et al., DMKD’2009]
Overall Acceptance
Criterion (OAC)
[Drutsa et al., CIKM’2015]

5. Major challenges in online evaluation
Major goal of online evaluation is to detect…
as many changes as possible as soon as possible
▌ Most changes do not affect the user experience dramatically
› So we have to move our service quality forward incrementally
› Hence we need to detect even very small effects
▌ The more changes we experiment with, the sooner we find a successful one
› We are limited in experimental units – all experiments share the same user traffic
› We need to detect those small effects with small experimental groups

6. Learning sensitive metric
combinations
Learning Sensitive Combinations of A/B Test Metrics.
Kharitonov, Drutsa, Serdyukov, WSDM 2017

7. Metric sensitivity
• One way to deal with those challenges  improve metric sensitivity
• But, all state-of-the-art online metrics used to detect changes are
simple and well-known “hand-made” statistics (proposed by
analytics, common sense, etc.)

8. Typical (per user) online metrics
• Number of sessions
• Session time
• Absence time
• Number of Clicks
• Clicks per query
• Number of queries
• Time to first click
Learn a “one-to-rule-them-all”
more sensitive metric
by combining them?

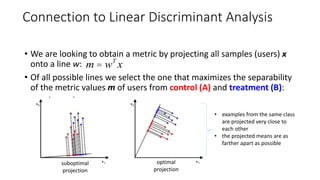
9. Learning sensitive combinations of metrics:
definitions
• Dataset of A/B tests (to be split into train and test sets):
• - experiments with known true preference direction (A > B/B > A) [very few]
• Regular experiments with high confidence outcome w.r.t. ground-truth metric
• Degradation experiments
• - experiments with unknown preference (not statistically significant) [numerous],
• - A/A experiments [numerous]
• Each observation unit (e.g., a user) is represented by a feature vector
• A feature can be an A/B test metric itself (e.g, mean session time), or…
• Some possibly useful characteristic of a user
xx
x Î Ân

10. Learning sensitive combinations of metrics:
problem statement
Given a dataset of experiments, , we aim to learn a vector of
weights such that the weighted combination of features (metrics)
• Is a useful metric itself:
• Respects preference relations in
• Is sensitive – optimizes Z-score:
x
m = wT
x
w x

11. Geometric approach: single experiment
(signed) Objective to maximize Z-score on a single experiment from
Optimal weights on a single experiment:
Covariance
matrix of the
features in B
Mean vector of the
features in A
Z(w;A, B) =
wT
xA - wT
xB
wT
åA w+ wT
åB w
we
*
µ(åA +åB +eI)×(xA - xB )

12. Connection to Linear Discriminant Analysis
• We are looking to obtain a metric by projecting all samples (users) x
onto a line w:
• Of all possible lines we select the one that maximizes the separability
of the metric values m of users from control (A) and treatment (B):
m = wT
x
suboptimal
projection
optimal
projection
• examples from the same class
are projected very close to
each other
• the projected means are as
farther apart as possible

13. Geometric approach: using multiple
experiments from the train set
• Average across multiple experiments, “balancing contribution“ from
each:

14. Optimization approach: utilizing all the data
Keep alternatives close in A/A experiments (keeping
Type I error low and reducing possible biases).
Separate alternatives
in A/B experiments
with low-confidence
outcomes, ignoring
sign
Increase sensitivity by separating A from B in
experiments with high confidence in the outcomes of
the experiments, penalizing changed preference sign
L-BFGS optimization of J(w) works well when initialized by Geometric approach
J(w) =
1
E
Z(w;Ae, Be )-a
1
CeÎE
å Z(w;Ac, Bc )
cÎC
å +
+b
1
U
Z(w;Au, Bu )
uÎU
å

15. One of the experiments
• Improving Sessions per User:
• Seed set contains experiments with statistical significance for Sessions per User
• All 8 metrics as features
• 10 fold cross-validation, nested cross-validation to adjust trade-off hyper-
parameters in the optimization approach
Median relative z-
score w.r.t. Sessions
per User
(relative sensitivity)
Sessions per User 1.00
Geometric 1.70
Optimization 3.42
3.422 ≈11 times less
data (median) to
achieve the same level
of confidence as
Sessions per User

16. Learning to predict for
Variance Reduction
Boosted Decision Tree Regression Adjustment
for Variance Reduction of Online Controlled Experiments.
Poyarkov, Drutsa, Khalyavin, Gusev, Serdykov, KDD 2016

17. Variance reduction = increase in sensitivity
Z-score =
YA -YB
s(YA )
|UA |
+
s(YB )
|UB |
The lower within-experiment metric variance – the higher the metric sensitivity

18. CUPED*: Controlled-experiment Using Pre-Experiment Data
It was suggested that the best X in terms of correlation is
the value of the same metric Y in the pre-experimental period
- linear regression on Y with one feature
Can we do better?
Our key metric Some random variable
* from Improving the Sensitivity of Online Controlled Experiments by Utilizing Pre-Experiment Data, WSDM 2013

19. Boosted Decision Tree Regression Adjustment
for Variance Reduction
(1) Apply advanced machine learning techniques
(like Gradient Boosted Decision Trees)
to predict the key metric for each user in the experimental period
(2) Using features that are user-level and
independent of the treatment assignment
(e.g., from pre-experimental period)
(3) Subtract the prediction for the key metric from
the actual value of the key metric
to obtain the new metric with reduced variance

20. Features used: 51 overall
• Total*: The metric value over the previous 14 days – 1 feature;
• TS: Time series of the previous 14 days – 27 features;
• CT: Cookie timestamps (creation time of the user’s cookie and the
users’ first entrance to the A/B test) – 3 features;
• TrTS: Transformed time series (Fourier Amplitudes, Entropies, etc.) –
20 features.
* Our baseline from Improving the Sensitivity of Online Controlled
Experiments by Utilizing Pre-Experiment Data, WSDM 2013

21. Results for Number of Sessions metric
Variance Reduction Rate Success Sensitivity Rate
Feature set Model
Linear
Regression
Decision Trees
Linear
Regression
Decision Trees
The source metric 1 (0%) 12 (7.45%)
Total
0.4337
(–56.63%)
0.4481
(–55.19%)
17
(10.55%)
18
(11.18%)
Total, TS
0.4108
(–5.27%)
0.4046
(–9.7%)
22
(13.66%)
21
(13.04%)
Total, TS, CT
0.3995
(–2.76%)
0.3743
(–7.49%)
19
(11.80%)
24
(14.91%)
All (Total, TS, CT, TrTS)
0.3935
(–1.5%)
0.3734
(–0.25%)
20
(12.42%)
24
(14.91%)
Comparison of feature sets and models in terms of
different performance evaluation over all studied A/B experiments
– baseline – – the best –

22. Future challenges
• Non-linear combinations of metrics
• Sparse combinations
• Metric combinations for variance reduction
• Future metric prediction to increase sensitivity:
• Future User Engagement Prediction and Its Application to Improve the
Sensitivity of Online Experiments. Drutsa, Gusev, Serdyukov. WWW 2015
• Using the Delay in a Treatment Effect to Improve Sensitivity and Preserve
Directionality of Engagement Metrics in A/B Experiments. Drutsa, Gusev,
Serdyukov. WWW 2017