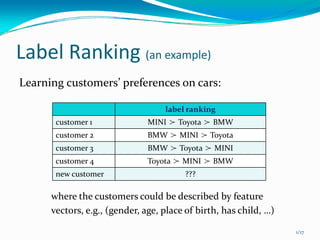
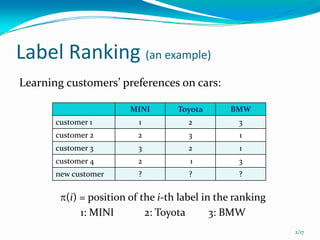
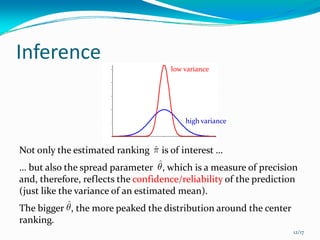
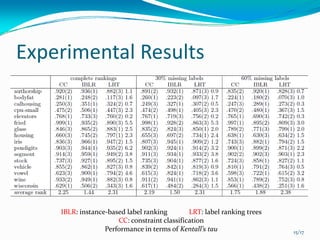
This document presents a local approach to label ranking using a probabilistic model. It describes an instance-based method for learning customers' preferences on cars from labeled training data consisting of customers' rankings of different car labels. The method models the distribution of rankings as locally constant, estimating the distribution from nearby preferences using maximum likelihood. It can handle both complete and incomplete rankings through an approximation of the EM algorithm. Experimental results show the local method can better exploit preference information than model-based approaches like constraint classification.

1. Weiwei Cheng, Jens Hühn and Eyke Hüllermeier
Knowledge Engineering & Bioinformatics Lab
Department of Mathematics and Computer Science
University of Marburg, Germany

2. Label Ranking (an example)
Learning customers’ preferences on cars:
label ranking
customer 1 MINI _ Toyota _ BMW
customer 2 BMW _ MINI _ Toyota
customer 3 BMW _ Toyota _ MINI
customer 4 Toyota _ MINI _ BMW
new customer ???
where the customers could be described by feature
vectors, e.g., (gender, age, place of birth, has child, …)
1/17

3. Label Ranking (an example)
Learning customers’ preferences on cars:
MINI Toyota BMW
customer 1 1 2 3
customer 2 2 3 1
customer 3 3 2 1
customer 4 2 1 3
new customer ? ? ?
π(i) = position of the i‐th label in the ranking
1: MINI 2: Toyota 3: BMW
2/17

4. Label Ranking (more formally)
Given:
a set of training instances
a set of labels
for each training instance : a set of pairwise preferences
of the form (for some of the labels)
Find:
A ranking function ( mapping) that maps each
to a ranking of L (permutation ) and generalizes well
in terms of a loss function on rankings (e.g., Kendall’s tau)
3/17

5. Existing Approaches
… essentially reduce label ranking to classification:
Ranking by pairwise comparison
Fürnkranz and Hüllermeier, ECML‐03
Constraint classification (CC)
Har‐Peled , Roth and Zimak, NIPS‐03
Log linear models for label ranking
Dekel, Manning and Singer, NIPS‐03
− are efficient but may come with a loss of information
− may have an improper bias and lack flexibility
− may produce models that are not easily interpretable
4/17

6. Local Approach (this work)
nearest neighbor decision tree
Target function is estimated (on demand) in a local way.
Distribution of rankings is (approx.) constant in a local region.
Core part is to estimate the locally constant model.
5/17

7. Local Approach (this work)
Output (ranking) of an instance x is generated according to a
distribution on
This distribution is (approximately) constant within the local
region under consideration.
Nearby preferences are considered as a sample generated by
which is estimated on the basis of this sample via ML.
6/17

8. Probabilistic Model for Ranking
Mallows model (Mallows, Biometrika, 1957)
with
center ranking
spread parameter
and is a right invariant metric on permutations
7/17

9. Inference (complete rankings)
Rankings observed locally.
ML
monotone in θ

10. Inference (incomplete rankings)
Probability of an incomplete ranking:
where denotes the set of consistent extensions of .
Example for label set {a,b,c}:
Observation σ Extensions E(σ)
a_b_c
a_b a_c_b
c_a_b
9/17

11. Inference (incomplete rankings) cont.
The corresponding likelihood:
Exact MLE becomes infeasible when
n is large. Approximation is needed.
10/17

12. 1 2 3 4
1 2 4 3
4 3
1 2 3 4
1 2 4 3
1 2 4 3
1 4 3
Inference (incomplete rankings) cont.
Approximation via a variant of EM, viewing the non‐observed
labels as hidden variables.
replace the E‐step of EM algorithm with a maximization step
(widely used in learning HMM, K‐means clustering, etc.)
1. Start with an initial center ranking (via generalized Borda count)
2. Replace an incomplete observation with its most probable
extension (first M‐step, can be done efficiently)
3. Obtain MLE as in the complete ranking case (second M‐step)
4. Replace the initial center ranking with current estimation
5. Repeat until convergence
11/17

13. Inference
low variance
high variance
Not only the estimated ranking is of interest …
… but also the spread parameter , which is a measure of precision
and, therefore, reflects the confidence/reliability of the prediction
(just like the variance of an estimated mean).
The bigger , the more peaked the distribution around the center
ranking.
12/17

14. Label Ranking Trees
Major modifications:
split criterion
Split ranking set into and , maximizing goodness‐of‐fit
stopping criterion for partition
1. tree is pure
any two labels in two different rankings have the same order
2. number of labels in a node is too small
prevent an excessive fragmentation
13/17

15. Label Ranking Trees
Labels: BMW, Mini, Toyota
14/17

16. Experimental Results
IBLR: instance‐based label ranking LRT: label ranking trees
CC: constraint classification
Performance in terms of Kentall’s tau 15/17

17. Accuracy (Kendall’s tau)
Typical “learning curves”:
0,8
0,75 LRT
Ranking performance
0,7
CC
0,65
0,6
Probability of missing label
0,55
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7
more amount of preference information less
Main observation: Local methods are more flexible and can exploit more
preference information compared with the model‐based approach.
16/17

18. Take‐away Messages
An instance‐based method for label ranking using a
probabilistic model.
Suitable for complete and incomplete rankings.
Comes with a natural measure of the reliability of a
prediction. Makes other types of learners possible:
label ranking trees.
o More efficient inference for the incomplete case.
o Dealing with variants of the label ranking problem, such as
calibrated label ranking and multi‐label classification.
17/17

19. Google “kebi germany” for more info.