Recommended
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PPTX
PPTX
PDF
PDF
RStanとShinyStanによるベイズ統計モデリング入門
PDF
PDF
一般化線形モデル (GLM) & 一般化加法モデル(GAM)
PDF
PDF
PDF
StanとRでベイズ統計モデリング 11章 離散値をとるパラメータ
PPTX
StanとRでベイズ統計モデリングに関する読書会(Osaka.stan) 第四章
PPTX
StanとRでベイズ統計モデリング読書会(Osaka.stan) 第6章
PDF
PDF
PDF
PDF
2 5 3.一般化線形モデル色々_Gamma回帰と対数線形モデル
PDF
PPTX
PDF
PDF
StanとRでベイズ統計モデリング読書会 Chapter 7(7.6-7.9) 回帰分析の悩みどころ ~統計の力で歌うまになりたい~
PDF
StanとRでベイズ統計モデリング読書会 導入編(1章~3章)
PDF
More Related Content What's hot
PDF
PPTX
PPTX
PDF
PDF
RStanとShinyStanによるベイズ統計モデリング入門
PDF
PDF
一般化線形モデル (GLM) & 一般化加法モデル(GAM)
PDF
PDF
PDF
StanとRでベイズ統計モデリング 11章 離散値をとるパラメータ
PPTX
StanとRでベイズ統計モデリングに関する読書会(Osaka.stan) 第四章
PPTX
StanとRでベイズ統計モデリング読書会(Osaka.stan) 第6章
PDF
PDF
PDF
PDF
2 5 3.一般化線形モデル色々_Gamma回帰と対数線形モデル
PDF
PPTX
PDF
PDF
StanとRでベイズ統計モデリング読書会 Chapter 7(7.6-7.9) 回帰分析の悩みどころ ~統計の力で歌うまになりたい~
Similar to StanとRでベイズ統計モデリング 1,2章
PDF
StanとRでベイズ統計モデリング読書会 導入編(1章~3章)
PDF
PPTX
NagoyaStat#7 StanとRでベイズ統計モデリング(アヒル本)4章の発表資料
PDF
PDF
PDF
20160311 基礎からのベイズ統計学輪読会第6章 公開ver
PDF
Rでベイズをやってみよう!(コワい本1章)@BCM勉強会
PDF
PDF
PPTX
PDF
Pattern Recognition and Machine Learning study session - パターン認識と機械学習 勉強会資料
PDF
PDF
Stanの紹介と応用事例(age heapingの統計モデル)
PPTX
PDF
PDF
PDF
PPTX
PDF
PDF
More from Miki Katsuragi
PDF
PDF
Vertex AI Gemini Prompt Engineering Tips
PDF
PDF
PDF
PDF
4_9 GCPUG女子会 Vertex Pipelines 101.pdf
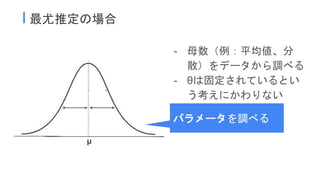
StanとRでベイズ統計モデリング 1,2章 1. 2. 3. 4. 5. 6. 7. 8. パラメータθはある一点の真の値を持つ定数と考える
I 伝統的な統計学の問題点
- 検定の解釈が直感的でない
- 仮説Hが正しいとした時にデータYかそれより極端なデータが得られる確
率(例:p(y>=Y|H))をp値と呼んで検定に使うが、p値は有意水準との比
較に使われるものなので直感的に解釈しにくい
- ベイズ統計はデータが得られた時の仮説Hが正しいかという確率p(H|Y)を
求めることができ、解釈しやすい。
- 信頼区間の解釈が直感的でない
- パラメータθは定数なので「θの値が区間[a,b]にある確率は95%である」
という言い方ができない
- 「データを取り直して解析を繰り返した時に『θの値が区間[a,b]にある』
と言えば95%くらい当たっているだろう」という解釈をしなければなら
ない
- 複雑なモデルにおいて信頼区間と予測区間の算出が難しい
- 複雑なモデルに含まれるパラメータの信頼区間や予測区間を求めるのは
理論的に難しく、数式も難解。
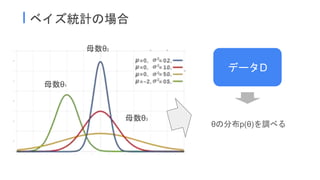
9. 10. 11. 12. ● 2項分布の確率関数は、本来成功回数xの関数
○ f(x|0.3) = 10Cx 0.3 (1-0.3)
○ 成功回数:変数 / 母数は定数=既知
● だが、(2.19)では以下のように定義される
○ f(4|0.3) = 10C4 0.3 (1-0.3)
○ 成功回数:定数 / 母数が変数=未知
x
(n−x)
4 (10−4)
現実世界ではデータ
(成功数)が固定されて
いるのでこちらが近
い(母数が既知なのは
サイコロなどに限ら
れてる)
確率0.3で成功するフリースローが10投中4回成功する確率は?
I 2項分布における尤度の例
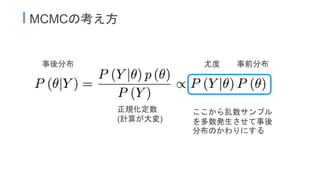
13. ● 確率関数の定数と変数を逆転して
○ f(x|θ)=nCx θ(1-θ)
● というようにθの関数と見た式を尤度関数と呼ぶ
○ θについて積分しても1にならない
○ 尤度が最大のときの変数θ=母数の推定値
● 確率は上記式をxの関数と見たもの
■ xについて足すと1になる
(n−x)
I 2項分布における尤度の例
14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. Editor's Notes #3 I How to : Editing Animated Interstitial Slides
Step 1 - Text
Replace the following text on this slide:
Title
Subtitle
Step 2 - Animated Slide
This is an animated interstitial slide, please do not move any content.
#5 I How to : Editing Animated Interstitial Slides
Step 1 - Text
Replace the following text on this slide:
Title
Subtitle
Step 2 - Animated Slide
This is an animated interstitial slide, please do not move any content.
#13 母数が既知なのはコインやサイコロ投げなど限られた場面のみ #15 あてはまりのよさを計算するときもカイ二乗値を計算するのに対数尤度を使う #18 I How to : Editing Animated Interstitial Slides
Step 1 - Text
Replace the following text on this slide:
Title
Subtitle
Step 2 - Animated Slide
This is an animated interstitial slide, please do not move any content.







![パラメータθはある一点の真の値を持つ定数と考える
I 伝統的な統計学の問題点
- 検定の解釈が直感的でない
- 仮説Hが正しいとした時にデータYかそれより極端なデータが得られる確
率(例:p(y>=Y|H))をp値と呼んで検定に使うが、p値は有意水準との比
較に使われるものなので直感的に解釈しにくい
- ベイズ統計はデータが得られた時の仮説Hが正しいかという確率p(H|Y)を
求めることができ、解釈しやすい。
- 信頼区間の解釈が直感的でない
- パラメータθは定数なので「θの値が区間[a,b]にある確率は95%である」
という言い方ができない
- 「データを取り直して解析を繰り返した時に『θの値が区間[a,b]にある』
と言えば95%くらい当たっているだろう」という解釈をしなければなら
ない
- 複雑なモデルにおいて信頼区間と予測区間の算出が難しい
- 複雑なモデルに含まれるパラメータの信頼区間や予測区間を求めるのは
理論的に難しく、数式も難解。](https://image.slidesharecdn.com/5trvkokirdgk6uqtcdfs-signature-ae1b36b0429380c374e80060e8382b52b46df4f016420bf89f9724af0dbe4b6d-poli-190815153650/85/Stan-R-1-2-8-320.jpg)