コース導入講義2015（荒木）

1. データ分析入門
楽しいプログラミング
E.ARAKI Faculty of Economics, Momoyama Gakuin University

2. プログラミング
❖ 狭義のプログラミング、広義のプログラミング
❖ いろんなプログラミング言語
C/C++
Java
Python Ruby PHP
R
Excel SPSS
難
易
OS コンパイル言語
スクリプト言語
（インタプリタ）
Webアプリケーション
HTML + Javascript
自分で工夫

3. R, Python : データ分析の主流言語
❖ R + Python : データサイエンティスト の最低要件
❖ いま、ビッグデータ がブーム
❖ 従来の（伝統的な）データ処理／分析手法ではうまくいかない
→ より高度なICT環境とツールが必要（分散処理、Non-SQL・・・）
→ データサイエンス（データサイエンティスト）
データサイエンスを実践するヒト
「21世紀で最もセクシーな職業」
3V : Volume（量、とてつもなくデカい）
Velocity（速度、どんどん更新されていく）
Variety（多様、いろんなカタチ）

4. ガートナーのハイプ・サイクル
❖ Buzzword（テクノロジ＝技術に関わる流行語）
の栄枯盛衰を図示したもの
颯爽と登場
注目をあびる
過剰な
期待の高まり
飽きられ
幻滅される
真価が徐々に
再評価される
社会に根付き
身近な技術に

5. ハイプサイクル2014
ハイプ・サイクル 2014 （ガートナー 2014年8月）
IoT : Internet of Things
いろんなモノが
ネットでつながる

6. ICT高度化の（データ分析への）恩恵
❖ 「よりカンタンに・より効率的に」「フリー free（自由、無料）」
❖ 【オープンデータ】公開の世界的な広がり
❖ 【ライブラリ（道具箱）】の充実（オープンソース、WebAPI）
❖ R の成熟, Python の勃興
❖ 可視化（見える化）の高度化 美しく精巧なグラフ
❖ 高度な分析もより容易に
❖ 積極的に活用しない手はない！
→ プログラミングの素養（基本作法）が必要
→ R ならカンタン、すぐにでも可
❖ Python ( OOP ) の修得には多少の時間がかかるが、得るモノは大きい。
実例 (Motion Chart) を見ましょう
http://rio.andrew.ac.jp/araki/gVisWB.html
( Google chart API + World Bank API ← R )

7. Motion Chart
library(WDI)
inds <- c('SP.DYN.TFRT.IN','SP.DYN.LE00.IN',
'SP.POP.TOTL','NY.GDP.PCAP.CD', 'SE.ADT.1524.LT.FE.ZS')
indnams <- c(“fertility.rate", “life.expectancy",
"population","GDP.per.capita.Current.USD",
"15.to.25.yr.female.literacy")
wdiData <- WDI(country="all",
indicator=inds,start=1960,end=format(Sys.Date(),"%Y"),extra=TRUE)
colnum <- match(inds, names(wdiData))
names(wdiData)[colnum] <- indnams
library(googleVis)
WorldBank <- droplevels(subset(wdiData, !region %in% "Aggregates"))
M <- gvisMotionChart(WorldBank,idvar="country",timevar="year",
xvar="life.expectancy",yvar="fertility.rate",
colorvar="region",sizevar="population",
options=list(width=700, height=600),chartid="WorldBank")
plot(M)
World Bank からデータ取得
Google Visualisation API を呼び出す

8. データ分析（統計分析）
❖ データ（標本）
❖ 代表値（平均とか偏差とか） クロス集計
❖ わかりやすい表 美しいグラフ
❖ データ（標本）やものごと（事象）の背後に潜むモノ
❖ 関係 法則 母集団特性
❖ シミュレーション 相関・回帰 予測
記述統計
推測統計

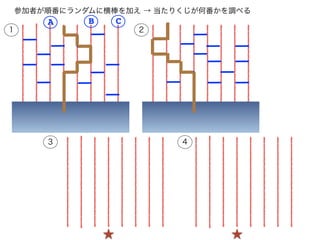
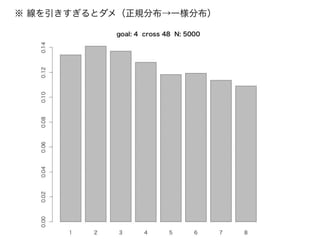
9. あみだくじ
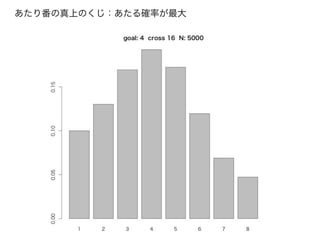
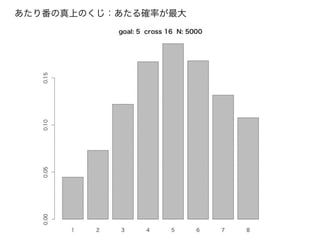
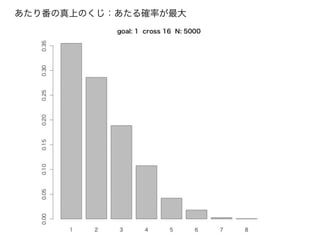
シミュレーションで、あみだくじの「必勝法」を知る
amidakuji <- function(ninzu=8,senbiki=2,goal=0) {
# ninzu: あみだくじに参加する人数（＝縦線の数）
# senbiki: 横棒（横移動の線）を一人何本引けるか
# goal: 終点のあたり番（0 ならランダムに決める）
sen = ninzu; dan = ninzu*2
x = matrix(0,nrow=dan,ncol=sen) # あみだくじの作成
k = 0; step = sen -1
while(k < ninzu*senbiki) {
i = sample(dan,size=1) ; j = sample(step,size=1)
if( x[i,j]==0 && x[i,j+1]==0 ) { x[i,j]=1; x[i,j+1]=-1; k = k+1 }
}
if(goal==0) goal=sample(sen,size=1) # 終点のあたり番（0ならランダムに）
atari = goal # あたりくじを終点から逆にたどっていく
for( i in dan:1) atari = atari + x[i,atari]
return(atari)
}

10. 参加者が順番にランダムに横棒を加え → 当たりくじが何番かを調べる
1 2
3 4
A B C

11. あたり番の真上のくじ：あたる確率が最大

12. あたり番の真上のくじ：あたる確率が最大

13. あたり番の真上のくじ：あたる確率が最大

14. ※ 線を引きすぎるとダメ（正規分布→一様分布）

15. データ分析（統計分析）
❖ データ（標本）
❖ 代表値（平均とか偏差とか） クロス集計
❖ わかりやすい表 美しいグラフ
❖ データ（標本）やものごと（事象）の背後に潜むモノ
❖ 関係 法則 母集団特性
❖ シミュレーション 相関・回帰 予測
記述統計
推測統計

16. 相関とは
• 相関とは・・・２つのモノ（変数）の関連のこと
タバコ喫煙量 肺がんで死ぬリスク 正相関（同方向の連動）
消費税率 人々の消費支出 負相関（逆方向の連動）
荒木の体重 日本の経済成長率 無相関（関係ナシ）
• 相関分析とは・・・以下のふたつを判定すること
• ２つのモノ（変数）が、正相関か 負相関か 無相関か
• どれくらい密接に（強く）連動しているか
• 相関係数（Correlation Coefficient）というツール

17. 相関係数とは
• 任意のふたつの変数（データ）のあいだで計算される、ある数値
• かならず、-1 から +1 までの範囲の、どこかの値となる
• 見方はカンタン、以下の図のとおり
相関係数の値 -1 0 +1
相関の方向 負相関 無相関 正相関
相関の強さ
強い 弱い 弱い 強い
-0.3 0.3-0.8 -0.5 0.90.40.1

18. プロ野球の分析 Excel
❖ 選手（打者選手）の年俸と相関がもっとも高いものは、出場試合数・打点・打率・
本塁打・盗塁数のうち、どれか？
❖ Excelで、実際にやってみましょう。
❖ substitute(A, B, C) 文字列Aに含まれる文字列Bを文字列Cに置換
❖ value(A） 文字列Aを数値に変換
❖ lookup(A,B,C) データ範囲BからAのレコードを検索、列Cの内容を返す
❖ correl(A,B) データAとデータBとの相関係数を計算する
❖ ある球団（タイガース）のある年（2013年）の分析だけでも、とても煩雑
全球団・過去のデータもあわせてとなると・・・分析しきれない

19. 同じ作業をRでやると・・・
t1 = read.csv("~/Desktop/Tigers2013-1.csv",head=T)
t2 = read.csv("~/Desktop/Tigers2013-2.csv",head=T)
dat = merge(t1,t2)
attach(dat)
年俸=as.numeric(gsub(‘万円’,'',年俸))
cor( cbind(年俸,試合,打率,打点,本塁打,盗塁) )
年俸 試合 打率 打点 本塁打 盗塁
年俸 1.0000000 0.6658899 0.3830028 0.8651618 0.7667111 0.4317489
試合 0.6658899 1.0000000 0.6311399 0.8519692 0.6757653 0.5791703
打率 0.3830028 0.6311399 1.0000000 0.4624384 0.3580283 0.4105070
打点 0.8651618 0.8519692 0.4624384 1.0000000 0.9315804 0.4523529
本塁打 0.7667111 0.6757653 0.3580283 0.9315804 1.0000000 0.2313036
盗塁 0.4317489 0.5791703 0.4105070 0.4523529 0.2313036 1.0000000

20. 回帰とは
• 回帰とは・・・予測のための方程式を求める手法
消費税が２%上がると、日本全体で消費支出がどれくらい減るか？
消費支出 ＝ 100 + 0.5 × 所得 - 0.3 × 価格
消費税（価格）が２％上がると → 消費支出はどれだけ減るか？
• Excelでは・・・
回帰分析は、アドインの分析ツールなどでいちおう可能
しかし・・・
* データがちょっと大きくなると、作業がとても煩雑
* 単純な回帰分析しかできない
（計量経済学の多様な回帰手法、最近の機械学習）
• プログラミング（R,Python）なら・・・
→ 作業は効率化（カンタンに）できる（ビッグデータに対応）
→ さまざまな最新手法が利用できる

21. さらに プロ野球の分析 R
❖ 選手（打者選手）の年俸と打点の関係式を求めてみよう。
summary( lm(年俸~1+打点) )
❖ 打点を1点増やすと、年俸はどれくらい上がるか？
❖ 一億円プレーヤになるためには、打点は何点必要か？
❖ 給料もらいすぎの選手、給料が少なすぎる選手は誰か？
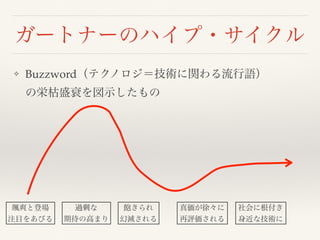
plot(打点,年俸）
abline(633.77,299.85,col=“red”)
identify(打点,年俸,選手名)
年俸 = 633.77 + 299.85 打点
(9.129)
R2 = 0.7485
299.85万円
10000=633.77+299.85*打点 " 打点=(10000-633.77)/299.85 = 31.3

23. 今日のまとめ
❖ ICT高度化により、データ分析は・・・
→「よりカンタンに・より効率的に」
→「フリー free（自由、無料）」
❖ 【オープンデータ】
❖ 【ライブラリ（道具箱）】の充実（オープンソース、WebAPI）
❖ R の成熟, Python の勃興
❖ 美しく精巧なグラフ、高度な分析もより容易に
❖ 積極的に活用しない手はない！
→ プログラミングの素養（基本作法）が必要
→ でも、R ならカンタン、すぐにでも可
❖ Python ( OOP ) の修得には多少の時間がかかるが、得るモノは大きい。