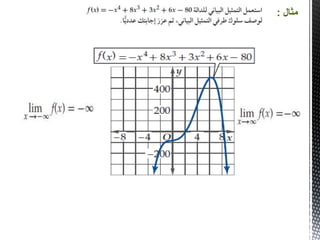
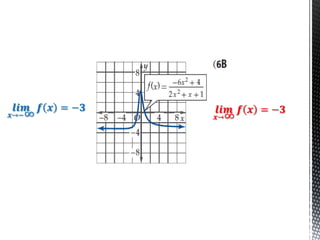
تتناول الوثيقة موضوع الاتصال في الدوال الرياضية، حيث تشرح متى تكون الدالة متصلة أو غير متصلة. كما تشمل الوثيقة أمثلة توضيحية حول كيفية التحقق من الاتصال عند النقاط المحددة. تُعتبر الحدود النهائية للدوال وتحليل سلوكها خلال الاقتراب من النقاط المحددة جزءًا أساسيًا من الفهم.


















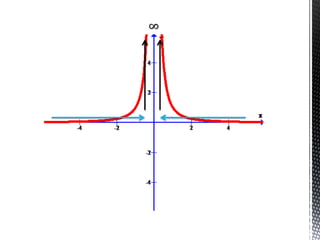



![[ -3 , -2 ]
[ 0 , 1 ]
[ 1 , 2 ]](https://image.slidesharecdn.com/random-141219065531-conversion-gate01/85/slide-26-320.jpg)
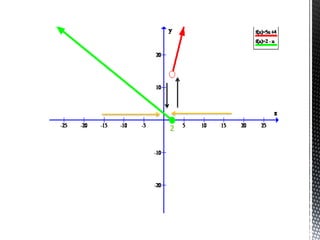
![صــــــ فهمك من تحقق31ـــــــــ(3A: )
43210-1-2-3-4-5-6x
67243-231219183-32-93f(x)
[ -5 , -4 ]
[ 0 , 1 ]
[ 1 , 2 ]](https://image.slidesharecdn.com/random-141219065531-conversion-gate01/85/slide-27-320.jpg)