1. อัตราส่วนของจํานวน
หลายๆจํานวน

2. จุดประสงค์การเรียนรู้
 เขียนอัตราส่วนแทนการเปรียบเทียบปริมาณของ
สิงต่างๆทีมากกว่า2 สิงขึนไปได้
 ใช้ความรู้เกียวกับอัตราส่วนของจํานวนหลายๆ
จํานวนในการแก้ปัญหาหรือสถานการณ์ต่างๆได้

3. ผงช็อคโกแลตมอลต์ ช้อนชา
นําตาล ช้อนชา
นมสด ช้อนชา
2
1
1
3
2

4. จากส่วนผสมของเครืองดืมรสช็อคโกแลตมอลต์
1 ถ้วย สามารถเขียนอัตราส่วนเปรียบเทียปริมาณ
ของส่วนผสมต่างๆ ได้ดังนี
จํานวนผงช็อคโกแลตมอลต์ต่อจํานวนนําตาลเป็น
:
จํานวนนําตาลต่อจํานวนนมสดเป็น
:
2
1
1 3
3 2

5. น อ ก จ า ก ก า ร เ ขี ย น อั ต ร า ส่ ว น แ ส ด ง
การเปรียบเทียบปริมาณของส่วนผสมทีละคู่แล้ว
เรายังสามารถเขียนอัตราส่วนแสดงการเปรียบเทียบ
ปริมาณของส่วนผสมทังหมดได้ดังนี
จํานวนผงช็อคโกแลตมอลต์ต่อจํานวนนําตาลต่อ
จํานวนนมสดเป็น : :
2
1
1 3 2
เราเรียกอัตราส่วนเช่นนีว่า
“อัตราส่วนของจํานวนหลายๆจํานวน”

6. นํามะนาว ช้อนโต๊ะ
นําเชือม ถ้วย
เกลือป่ น ช้อนชา
2
1
4
1

7. จากส่วนผสมของนํามะนาว เราสามารถเขียน
อัตราส่วนเปรียบเทียบปริมาณของส่วนผสมต่างๆ ได้
ดังนี
จํานวนนํามะนาวเป็ นช้อนโต๊ะต่อจํานวนนําเชือม
เป็นถ้วยต่อจํานวนเกลือป่ นเป็นช้อนชา
เท่ากับ : :2 1 4
1

8. เราเรียกอัตราส่วนเช่นนีว่า
“อัตราส่วนของจํานวนหลายๆจํานวน”
หรืออาจเขียนว่า
จํานวนนํามะนาวต่อจํานวนนําเชือมต่อจํานวน
เกลือป่ นเป็น ช้อนโต๊ะต่อ ถ้วยต่อ ช้อนชา2 1
4
1

9. อัตราส่วนของจํานวนหลายๆ
จํานวนเกิดจาก...
การนําปริมาณของสิ งต่างๆที มากกว่า2 สิ งขึนไป
มาเปรียบเทียบกัน โดยตําแหน่งของจํานวนในอัตราส่วน
ของจํานวนหลายๆจํานวนมีความสําคัญ

10. เมือมีอัตราส่วนสองอัตราส่วนใดๆทีแสดง
การเปรียบเทียบปริมาณของสิงสามสิงเป็ นคู่ๆ
เราสามารถเขียนอัตราส่วนของจํานวนทังสาม
จํานวนจากสองอัตราส่วนเหล่านัน ด้วยการทํา
ปริมาณของสิงทีเป็นตัวร่วมในสองอัตราส่วนให้
เป็ นปริมาณทีเท่ากัน โดยใช้หลักการหา
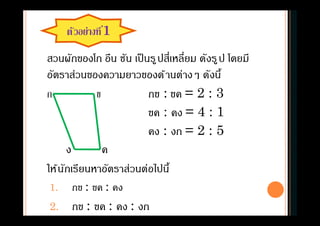
อัตราส่วนทีเท่ากัน

11. ตัวอย่างที1
สวนผักของโก อึน ชัน เป็นรูปสีเหลียม ดังรูป โดยมี
อัตราส่วนของความยาวของด้านต่างๆ ดังนี
ก ข กข : ขค = 2 : 3
ขค : คง = 4 : 1
คง : งก = 2 : 5
ง ค
ให้นักเรียนหาอัตราส่วนต่อไปนี
1. กข : ขค : คง
2. กข : ขค : คง : งก

12. ตัวอย่างที 1 ข้อ 1 เขียนอัตราส่วนแสดงความยาว
ของด้านใดบ้าง
อัตราส่วนของด้าน กข: ขค เป็นเท่าไร
อัตราส่วนของด้าน ขค: คง เป็นเท่าไร
อัตราส่วนสองอัตราส่วนนีมีด้านใดเป็นด้านร่วม
ท้าทาย...ท้านาย

13. ถ้าอัตราส่วนต้องการเขียนอัตราส่วนของด้าน
กข : ขค : คง นักเรียนต้องทําให้ความยาวของด้าน
ร่วม คือ ด้าน ขค ของทังสองอัตราส่วนเท่ากันใช่
หรือไม่
นักเรียนทําให้ความยาวด้าน ขค ซึงเป็ นด้านร่วมยาว
เท่าไร
อัตราส่วนของด้าน กข: ขค : คง เป็นเท่าไร

14. กข : ขค : คง
วิธีทํา
เนืองจาก กข : ขค = 2 : 3 และ ขค : คง = 4 : 1
จาก กข : ขค และ ขค : คง ด้านร่วม คือ ด้าน ขค
หา ค.ร.น. ของ 3 กับ 4 คือ 12
จะได้ว่า กข : ขค = 2 4 : 3 4
และ ขค : คง = 4 3 : 1 3
ดังนัน กข : ขค : คง = 8 : 12 : 3
 
 

15. ตัวอย่างที 1 ข้อ 2 เขียนอัตราส่วนแสดงความยาวของ
ด้านใดบ้าง
อัตราส่วนของด้าน กข: ขค : คง เป็นเท่าไร
อัตราส่วนของด้าน คง: งก เป็นเท่าไร
อัตราส่วนสองอัตราส่วนนีมีด้านใดเป็นด้านร่วม
ท้าทาย...ท้านาย

16. ถ้าอัตราส่วนต้องการเขียนอัตราส่วนของด้าน กข: ขค :
คง : งก นักเรียนต้องทําให้ความยาวของด้านร่วม คือ ด้าน คง
ของทังสองอัตราส่วนเท่ากันใช่หรือไม่
นักเรียนทําให้ความยาวด้าน คง ซึงเป็นด้านร่วมยาวเท่าไร
อัตราส่วนของด้าน กข: ขค : คง : งก เป็นเท่าไร

17. กข : ขค : คง : งก
วิธีทํา
เนืองจาก กข : ขค : คง = 8 : 12 : 3
และ คง : งก = 2 : 5
จาก กข : ขค : คง และ คง : งก
ด้านร่วม คือ ด้าน คง
หา ค.ร.น. ของ 3 กับ 2 คือ 6

18. จะได้ กข : ขค : คง = 8 2 : 12 2 : 3 2
= 16 : 24 : 6
และ คง : งก = 2 3 : 5 3
= 6 : 15
ดังนัน กข : ขค : คง : งก
= 16 : 24 : 6 : 15
  
 

19. จากอัตราส่วนของจํานวนหลายๆจํานวน
a : b : c เราสามารถเขียนอัตราส่วนของจํานวน
ทีละสองจํานวนได้เป็นa : b และ b : c
เมือ m แทนจํานวนใดๆ
จะได้ว่าa : b = am : bm
และ b : c = bm : cm
ดังนันa : b : c = am : bm : cm
เมือ m แทนจํานวนบวก

20. ในทํานองเดียวกัน ถ้ามีอัตราส่วนทีมากกว่า
สามจํานวนก็สามารถใช้หลักการเดียวกันนี เช่น
ดังนันa : b : c : d = am : bm
: cm : dm เมือ m แทนจํานวนบวก

23. อัตราส่วนของความสูงของเป๊ กต่อความสูงของอ๊อฟ
เป็น 3 : 2 และอัตราส่วนของความสูงของอ๊อฟต่อ
ความสูงของไอซ์เป็น4 : 5
นักเรียนจะเขียนอัตราส่วนแสดงการเปรียบเทียบ
ความสูงของเป๊ กต่อความสูงของอ๊อฟต่อความสูงของไอซ์
ได้อย่างไร
ทบทวน...สักนิด

24. ท้าทาย...ท้านาย

25. ภาขวัญชอบสะสมเครืองเขียน จํานวนเครืองเขียนที
ภาขวัญสะสมไว้มีดังนี จํานวนดินสอต่อจํานวนยางลบเป็ น
2 : 3 จํานวนยางลบต่อจํานวนปากกาเป็น5 : 7
จงเขียนอัตราส่วนของจํานวนดินสอ
ต่อจํานวนยางลบต่อจํานวนปากกาทีภาขวัญ
สะสมไว้

26. การแก้ปัญหา
1. ทําความเข้าใจปัญหา
โจทย์ต้องการทราบอะไร
โจทย์กําหนดข้อมูลอะไรบ้าง
โจทย์ต้องการทราบอัตราส่วนของจํานวนดินสอต่อ
จํานวนยางลบต่อจํานวนปากกาทีภาขวัญสะสมไว้
อัตราส่วนของจํานวนดินสอต่อจํานวนยางลบเป็น2 : 3
และอัตราส่วนของจํานวนยางลบต่อจํานวนปากกาเป็น
5 : 7

27. ตัวร่วมของอัตราส่วนของจํานวนดินสอต่อจํานวน
ยางลบและอัตราส่วนของจํานวนยางลบต่อจํานวน
ปากกา คืออะไร
จํานวนยางลบ

28. นักเรียนจะมีวิธีการอย่างไรในการทําให้ปริมาณของตัวร่วม
ในแต่ละอัตราส่วนมีปริมาณเท่ากัน
2. วางแผนแก้ปัญหา
ใช้หลักการหาอัตราส่วนทีเท่ากัน

29. เนืองจากจํานวนยางลบเป็นตัวร่วมจึงหา ค.ร.น. ของ 3 กับ
5 ซึงเท่ากับ15
ดังนัน อัตราส่วนของจํานวนดินสอต่อจํานวนยางลบ
เท่ากับ2 : 3 = 2×5 : 3×5
= 10 : 15
อัตราส่วนของจํานวนยางลบต่อจํานวนปากกา
เท่ากับ5 : 7 = 5×3 : 7×3
= 15 : 21
3. ดําเนินการแก้ปัญหา
ดังนัน อัตราส่วนของจํานวนดินสอต่อจํานวนยางลบ
ต่อจํานวนปากกาเท่ากับ 10 : 15 : 21

30. ตรวจสอบขั นตอนการคํานวณ ความสอดคล้องของ
คําตอบกับเงือนไขต่างๆทีกําหนดในปัญหาคือ
อัตราส่วนของจํานวนดินสอต่อจํานวนยางลบเป็น2 : 3
และอัตราส่วนของจํานวนยางลบต่อจํานวนปากกาเป็น5 : 7
อัตราส่วนของจํานวนดินสอต่อจํานวนยางลบต่อจํานวน
ปากกา เท่ากับ10 : 15 : 21 สามารถพิจารณาอัตราส่วน
ของจํานวนดินสอต่อจํานวนยางลบต่อจํานวนปากกาเป็นคู่ ได้ดังนี
4. ตรวจสอบคําตอบ

31. อัตราส่วนของจํานวนดินสอต่อจํานวนยางลบเท่ากับ10 : 15
= 10÷5 : 3÷5
= 2 : 3
อัตราส่วนของจํานวนยางลบต่อจํานวนปากกาเท่ากับ15 : 21
= 15÷3 : 21÷3
= 5 : 7
ซึงสอดคล้องกับเงือนไขทีกําหนดในปัญหา ดังนัน คําตอบถูกต้อง

32. เนืองจากจํานวนยางลบเป็นตัวร่วมจึงหา ค.ร.น. ของ 3
กับ5 ซึงเท่ากับ15
ดังนัน อัตราส่วนของจํานวนดินสอต่อจํานวนยางลบ
เท่ากับ2 : 3 = 2×5 : 3×5
= 10 : 15
อัตราส่วนของจํานวนยางลบต่อจํานวนปากกา
เท่ากับ5 : 7 = 5×3 : 7×3
= 15 : 21
5. เขียนแสดงวิธีแก้ปัญหา
ดังนัน อัตราส่วนของจํานวนดินสอต่อจํานวนยางลบ
ต่อจํานวนปากกาเท่ากับ10 : 15 : 21

34. แบบฝึกหัด 1.3
(ทําข้อ 1 , 3 , 6 , 8)
ส่ง วันอังคาร ก่อน12:00 น .