หน่วยที่1อัตราส่วนสัดส่วนและร้อยละ

หน่ว ยที่ 1
อัต ราส่ว น สัด ส่ว นและร้อ ยละ
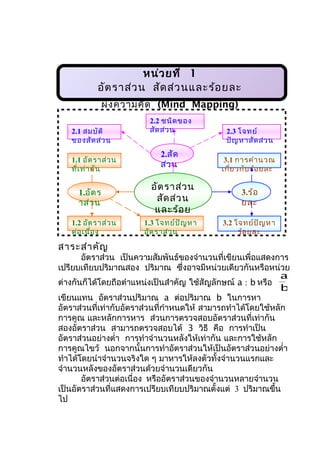
ผัง ความคิด (Mind Mapping)
2.2 ชนิด ของ
2.1 สมบัต ิ สัด ส่ว น 2.3 โจทย์
ของสัด ส่ว น ปัญ หาสัด ส่ว น
2.สัด
1.1 อัต ราส่ว น 3.1 การคำา นวณ
ที่เ ท่า กัน
ส่ว น เกี่ย วกับ ร้อ ยละ

อัต ราส่ว น
1.อัต ร 3.ร้อ
าส่ว น สัด ส่ว น ยละ
และร้อ ย
1.2 อัต ราส่ว น ละ
1.3 โจทย์ป ัญ หา 3.2 โจทย์ป ัญ หา
ต่อ เนื่อ ง อัต ราส่ว น ร้อ ยละ

สาระสำา คัญ
อัตราส่วน เป็นความสัมพันธ์ของจำานวนที่เขียนเพื่อแสดงการ
เปรียบเทียบปริมาณสอง ปริมาณ ซึ่งอาจมีหน่วยเดียวกันหรือหน่วย
a
ต่างกันก็ได้โดยถือตำาแหน่งเป็นสำาคัญ ใช้สัญลักษณ์ a : b หรือ
b
เขียนแทน อัตราส่วนปริมาณ a ต่อปริมาณ b ในการหา
อัตราส่วนที่เท่ากับอัตราส่วนที่กำาหนดให้ สามารถทำาได้โดยใช้หลัก
การคูณ และหลักการหาร ส่วนการตรวจสอบอัตราส่วนที่เท่ากัน
สองอัตราส่วน สามารถตรวจสอบได้ 3 วิธี คือ การทำาเป็น
อัตราส่วนอย่างตำ่า การทำาจำานวนหลังให้เท่ากัน และการใช้หลัก
การคูณไขว้ นอกจากนั้นการทำาอัตราส่วนให้เป็นอัตราส่วนอย่างตำ่า
ทำาได้โดยนำาจำานวนจริงใด ๆ มาหารให้ลงตัวทั้งจำานวนแรกและ
จำานวนหลังของอัตราส่วนด้วยจำานวนเดียวกัน
อัตราส่วนต่อเนื่อง หรืออัตราส่วนของจำานวนหลายจำานวน
เป็นอัตราส่วนที่แสดงการเปรียบเทียบปริมาณตั้งแต่ 3 ปริมาณขึ้น
ไป

2

สัดส่วน คืออัตราส่วนสองอัตราส่วนที่เท่ากัน สำาหรับการ
หาค่าของตัวแปรในสัดส่วน ใช้หลักการคูณไขว้และการแก้
สมการ
ร้อยละหรือเปอร์เซ็นต์ คือการเปรียบเทียบจำานวนใด
จำานวนหนึ่งกับ 100 โดยใช้หลักการ ของอัตราส่วนที่มีจำานวนหลัง
เป็น 100 โดยเปลี่ยนรูประหว่างร้อยละ เศษส่วน และทศนิยมได้
รวมทั้งสามารถนำาความรู้เรื่องสัดส่วนมาใช้ในการแก้โจทย์ปัญหา
เกี่ยวกับร้อยละได้
สาระการเรีย นรู้
1. อัต ราส่ว น
1.1 อัตราส่วนที่เท่ากัน
1.2 อัตราส่วนต่อเนื่อง
1.3 โจทย์ปัญหาอัตราส่วนในงานอาชีพและชีวิตประจำา
วัน
2. สัด ส่ว น
2.1 สมบัตของสัดส่วน
ิ
2.2 ชนิดของสัดส่วน
2.3 โจทย์ปัญหาสัดส่วนในงานอาชีพและชีวิตประจำา
วัน
3. ร้อ ยละ
3.1 การคำานวณเกี่ยวกับร้อยละ
3.2 โจทย์ปัญหาร้อยละในงานอาชีพและชีวิตประจำาวัน

จุด ประสงค์ก ารเรีย นรู้
1. อธิบายความหมายและเขียนอัตราส่วนได้ถูกต้อง
2. คำานวณค่าอัตราส่วนที่เท่ากับอัตราส่วนที่กำาหนดให้ได้
3. คำานวณค่าอัตราส่วนอย่างตำ่าของอัตราส่วนที่กำาหนดให้
ได้
4. เขียนอัตราส่วนต่อเนื่องจากอัตราส่วนหลายอัตราส่วนที่
กำาหนดให้ได้
5. แก้โจทย์ปัญหาเกี่ยวกับอัตราส่วนในงานอาชีพและชีวิต
ประจำาวันได้
6. อธิบายความหมายของสัดส่วนได้ถูกต้อง
7. คำานวณค่าตัวแปรในสัดส่วนที่กำาหนดให้ได้

3

8. แก้โจทย์ปัญหาเกี่ยวกับสัดส่วนในงานอาชีพและชีวิต
9. อธิบายความหมายของร้อยละได้ถูกต้อง
10. เปลี่ยนร้อยละให้อยู่ในรูปเศษส่วนหรือทศนิยมได้
11. เปลี่ยนเศษส่วนหรือทศนิยมให้อยู่ในรูปร้อยละได้
12. แก้โจทย์ปัญหาเกี่ยวกับร้อยละในงานอาชีพและชีวิต
13. มีคุณธรรม จริยธรรม และคุณลักษณะอันพึงประสงค์
ในชีวิตประจำาวันและวิชาชีพ ต้องนำาความรู้เกี่ยวกับ
อัตราส่วน มาใช้ประโยชน์เพื่อเปรียบเทียบหรือระหว่างปริมาณ
ต่าง ๆ เช่น อัตราส่วนการลงทน การลงทุน การผสมปุ๋ยและสาร
เคมี การออกแบบ การก่อสร้าง สูตรอาหาร นำาไปใช้กับเรื่อง
สัดส่วน ร้อยละ และอื่น ๆ ที่เกี่ยวข้องอีกมากมาย ดังนั้น
อัตราส่วนจึงมีความสำาคัญที่จะต้องเรียนรู้ให้เข้าใจและสามารถนำา
ไปใช้ได้อย่างถูกต้องและเหมาะสม

1. อัต ราส่ว น (Ratio)
ความหมายของอัต ราส่ว น
อัต ราส่ว น เป็นความสัมพันธ์ของจำานวนที่เขียนเพื่อ
แสดงการเปรียบเทียบปริมาณสองปริมาณ ซึ่งอาจมีหน่วย
a
เดียวกันหรือหน่วยต่างกันก็ได้ ใช้สัญลักษณ์ a : b หรือ
b
เขียนแทน อัตราส่วนปริมาณ a ต่อปริมาณ b ซึ่งแต่ละจำานวน
ในอัตราส่วนเป็นจำานวนบวกเท่านั้น
เรียก a ว่าจำานวนแรก หรือจำานวนที่หนึ่งของ
อัตราส่วน
เรียก b ว่าจำานวนหลัง หรือจำานวนที่สองของ
ตำาแหน่งของจำานวนในแต่ละอัตราส่วนมีความสำาคัญ
การสลับตำาแหน่งกันจะได้อัตราส่วนที่ต่างกัน เช่น อัตราส่วน
3 : 5 ไม่ใช่อัตราส่วนเดียวกับอัตราส่วน 5 : 3 นอกจากนี้ ยัง
ใช้อัตราส่วนเขียนแทนอัตราได้ด้วย เนื่องจากอัตรา เป็น
ข้อความที่แสดงความเกี่ยวข้องของปริมาณสองปริมาณ (หรือ
มากกว่า 2 ปริมาณ) และใช้อัตราส่วนแทน เช่น

4

ข้อความ อัตรา อัตราส่ว
น
รถยนต์ 1 คัน นั่งได้ 4 คน 1 คัน นั่งได้ 4 1:4
คน
โทรศัพท์ 3 ครั้ง จ่ายเงิน 6 3 ครั้ง ราคา 6 3:6
บาท บาท
เงิน 24 บาท ซื้อนำ้าอัดลมได้ 2 24 บาท ซือได้
้ 24 : 2
ขวด 2 ขวด
ส้มเขียวหวาน 40 ผล บรรจุได้ 40 ผล บรรจุได้ 40 : 2
2 กล่อง 2 กล่อง
พิทักษ์ขับรถด้วยความเร็ว 130 130 กิโลเมตรต่อ 130 :
กิโลเมตรต่อชั่วโมง 1 ชั่วโมง 1
วิธ ีเ ขีย นอัต ราส่ว น มี 2 วิธ ีด ัง นี้
วิธ ีท ี่ 1 การเปรียบเทียบปริมาณที่มีห น่ว ยเหมือ นกัน
ไม่นิยมเขียนหน่วยกำากับไว้ เช่น
- สมชายมีเงิน 25 บาท สมหญิงมีเงิน 40 บาท
ดัง นั้น อัตราส่วนจำานวนเงินสมชายต่อจำานวนเงินสม
หญิง เท่า กับ 25 : 40
หรือ 5:
8
- ผ้าผืนหนึ่งมีด้านยาวยาว 1.2 เมตร ด้านกว้าง
ยาว 60 เซนติเ มตร
1 เมตร เท่ากับ 100 เซนติเมตร
เปลี่ย นหน่ว ยทีต่างกันจาก
่ 1.2 เมตร เท่ากับ
1.2 × 100 = 120 เซนติเมตร เมตรให้เ ป็น
เซนติเ ม ตร
ดัง นั้น อัตราส่วนด้านยาวต่อด้านกว้าง เท่า กับ
120 : 60
หรือ 2:1
วิธ ีท ี่ 2 การเปรียบเทียบปริมาณที่มีห น่ว ยต่า งกัน ต้อง
เขียนหน่วยกำากับไว้ เช่น
- ซือขนมปังราคาปอนด์ละ 100 บาท
้

5

ดัง นั้น อัตราส่วนนำ้าหนักขนมปังเป็นปอนด์ต่อราคา
เป็นบาท เท่า กับ 1 : 100
- เนื้อที่ 1 ตารางเมตร ใช้กระเบื้อง 145 แผ่น
ดัง นั้น อัตราส่วนเนื้อที่เป็นตารางเมตรต่อจำานวน
กระเบื้องเป็นแผ่น
เท่า กับ 1 : 145
♣ ..หมายเหตุ อัตราส่วนนิยมเขียนเป็นอัตราส่วนอย่างตำ่า
การหาอัต ราส่ว นที่เ ท่า กับ อัต ราส่ว นที่ก ำา หนดให้
เมื่อกำาหนดอัตราส่วน a : b มีอัตราส่วนอื่น ๆ มากมาย
ที่เท่ากับอัตราส่วน a : b
ซึ่งหาได้จาก
หลัก การคูณ ทำาได้โดยการนำาจำานวนเดียวกันที่ไม่
เท่ากับศูนย์ คูณจำานวนหน้าและจำานวนหลังของอัตราส่วน a : b
a :b = ac:bc
a a× c เมื่อ c ≠ 0
b= b c
×
หลัก การหาร ทำาได้โดยการนำาจำานวนเดียวกันที่ไม่
เท่ากับศูนย์ หารจำานวนหน้าและจำานวนหลังของอัตราส่วน a : b
a:b = a÷ c:b÷ c
เมื่อ c ≠ 0
a a÷ c
b= b÷ c
จากหลักการหาอัตราส่วนที่เท่ากับอัตราส่วนที่กำาหนดให้ดัง
กล่าว สามารถสรุปได้ดังนี้

6

อัต ราส่ว นที่ก ำา หนด หลัก อัต ราส่ว นที่เ ท่า กับ
ให้ การ อัต ราส่ว นที่ก ำา หนดให้
2:3 22:32 = 4:6
23:33 = 6:9
2  4 : 3  4 = 8 : 12
2  5 : 3  5 = 10 : 15
คูณ ฯลฯ
5:7 5  5 : 7  5 = 25 : 35
5  40 : 7  40 = 200 :
280
5  100 : 7  100 =
500 : 700
ฯลฯ
20 : 60 20 ÷ 2 : 60 ÷ 2 = 10 :
30
20 ÷ 4 : 60 ÷ 4 = 5 :15
20 ÷ 5 : 60 ÷ 5 = 4 :12
หาร 20 ÷ 10 : 60 ÷ 10 = 2 :
40 : 200 6
40 ÷ 10 : 200 ÷ 10 = 4
: 20
40 ÷ 20 : 200 ÷ 20 = 2
: 10
40 ÷ 8 : 200 ÷ 8 = 5 :
25
40 ÷ 4 : 200 ÷ 4 = 10 :
50
40 ÷ 2 : 200 ÷ 2 = 20 :
100
ตัว อย่า งที่ 1 จงหาอัตราส่วนที่เท่ากับอัตราส่วนที่กำาหนดให้
มาอีก 3 อัตราส่วน

7

1.1 3:5
1.2 0.004 : 0.1
1.3 1.25 : 3.75
1.1 3 : 5
♠..แนวทางการคิด ....จากโจทย์เขียนอัตราส่วนในรูปเศษส่วน
แล้วใช้ตัวคูณเป็นจำานวนเต็มบวกตัวใดก็ได้คููณทั้งเศษและส่วน
อาจเป็นตัวคูณที่เรียงหรือไม่เรียงกัน

3
วิธ ีท ำา 3:5 =
5
3 32 6
×
5 5 2= 10
=
×
3 33 9
×
5 5 3= 15
=
×
3 3 5 15
×
5 5 5= 25
=
×
ดัง นั้น อัต ราส่ว นที่เ ท่า กัน กับ อัต ราส่ว น 3 : 5 คือ
6 : 10 , 9 : 15 , 15 : 25
1.2 0.004 : 0.1
♠..แนวทางการคิด ....จากโจทย์อัตราส่วนไม่ใช่จำานวนเต็ม ให้
เขียนอัตราส่วนในรูปเศษส่วนแล้วเปลี่ยนอัตราส่วนใหม่ที่มีจำานวน
หน้าและจำานวนหลังเป็นจำานวนเต็ม ใช้ได้ทั้งตัวหารและตัวคูณ
เป็นจำานวนเต็มบวก หารและคููณทั้งเศษและส่วน
0.004 ×1,000
0.004 4
วิธ ีท ำา =
0.1 0.11,000
×
=
100
4 4÷ 4 1
1001004= 25
=
÷
4 4× 2 8
1001002= 200
=
×

8

4 4× 3 12
100100 = 300
=
×3
ดัง นั้น อัต ราส่ว นที่เ ท่า กับ อัต ราส่ว น 0.004 : 0.1
คือ 1 : 25 , 8 : 200 , 12 : 300
1.3 1.25 : 3.75
♠..แนวทางการคิด ....จากโจทย์อัตราส่วนไม่ใช่จำานวนเต็ม ให้
เขียนอัตราส่วนในรูปเศษส่วนแล้วเปลี่ยนอัตราส่วนใหม่ที่มีจำานวน
หน้าและจำานวนหลังเป็นจำานวนเต็ม ใช้ตัวหารเป็นจำานวนเต็ม
บวกตัวใดก็ได้ ที่หารลงตัวทั้งเศษและส่วน
1.25 × 100125
1.25
วิธ ีท ำา =
3.75 =
3.75 × 100375
1251255 25
÷
3753755= 75
=
÷
12512525 5
÷
= =
37537525 15
÷
125125 25 1
÷1
= =
375375 25 3
÷1
ดัง นั้น อัต ราส่ว นที่เ ท่า กับ อัต ราส่ว น 1.25 : 3.75
คือ 25 : 75 , 5 : 15 , 1 : 3
♣ ..หมายเหตุ 1. หลักการคูณสามารถใช้หาอัตราส่วนที่เท่ากับ
อัตราส่วนที่กำาหนดให้ ได้มากกว่าใช้หลักการหาร
2. ควรใช้หลักการคูณ ถ้าอัตราส่วนที่กำาหนดให้เป็น
อัตราส่วนอย่างตำ่า และควรใช้หลักการหาร (ลงตัว) ถ้า
อัตราส่วนที่กำาหนดให้เป็นอัตราส่วนที่เปรียบเทียบจำานวนที่มีค่า
มาก ๆ
3. อัตราส่วนบางอัตราส่วน ไม่สามารถนำาอัตราส่วนที่
เท่ากับอัตราส่วนนั้นมาใช้ได้ เพราะ เมื่อนำามาใช้แล้วจะทำาให้
ความหมายผิดไป เช่น การแข่งขันกีฬา จากข้อความ “ทีม
เทนนิสวิทยาลัย เทคนิคเพชรบูรณ์ ชนะ 2 : 1 เซต” เมื่อนำามา
เขียนในรูปอัตราส่วนจะได้ อัตราส่วนจำานวนเซตที่ทีมเทนนิส
วิทยาลัยเทคนิคเพชรบูรณ์ ชนะต่อแพ้เป็น 2 : 1 ซึ่งหมายความ

9

ว่าในการแข่งขันเทนนิส 3 เซต ทีมเทนนิสวิทยาลัยเทคนิค
เพชรบูรณ์ ชนะ 2 เซต และ แพ้ 1 เซต ถ้าเราหาอัตราส่วนที่
เท่ากับ 2 : 1 เป็น 4 : 2 ไม่ได้หมายความว่า ในการแข่งขัน
เทนนิส 6 เซต ทีมเทนนิสวิทยาลัยเทคนิคเพชรบูรณ์ จะต้อง
ชนะ 4 เซต และ แพ้ 2 เซต
1 2
ตัว อย่า งที่ 2 จงหาอัตราส่วนที่เท่ากับอัตราส่วน 2  45
5
มาอีก 3 อัตราส่วน
♠ ..แนวทางการคิด ....จากโจทย์อัตราส่วนอยู่ในรูปจำานวนคละ
ให้ทำาเป็นเศษเกิน ใช้การหารเศษส่วน โดยการเปลี่ยน
เครื่องหมายหาร เป็นเครื่องหมายคูณ กลับเศษเป็นส่วน กลับ
ส่วนเป็นเศษของตัว หาร..ใช้หลักการคูณและหลักการหาร..หา
อัตราส่วนใหม่ที่มีค่าเท่ากัน
1 2 11 22
วิธ ีท ำา 2 : 45 = 5 : 5
5
11 22 11 5 11
=
5 ÷ 5 = 5× 22 =
22
11 11 11 1
÷
= 22 11 =
22 ÷ 2
11 11 2
× 22
= 22 2 =
22 × 44
11 113
× 33
= 22 3 =
22 × 66
1 2
ดัง นั้น อัต ราส่ว นที่เ ท่า กับ อัต ราส่ว น 2  45
5
คือ 1 : 2 , 22 : 44 , 33 : 66
1.1 อัต ราส่ว นที่เ ท่า กัน
อัต ราส่ว นที่เ ท่า กัน เป็นอัตราส่วนสองอัตราส่วนใด ๆ
ที่ทำาให้เป็นอัตราส่วนอย่างตำ่าแล้ว จะได้อัตราส่วนทั้งสองที่มีค่า
เท่ากัน ในการตรวจสอบการเท่ากันของอัตราส่วนสองอัตราส่วน
ที่กำาหนดให้ สามารถตรวจสอบได้ 3 วิธี ดังนี้
วิธ ีท ี่ 1 ทำา เป็น อัต ราส่ว นอย่า งตำ่า

10

ขั้นที่ 1 เขียนอัตราส่วนให้อยู่ในรูปอัตราส่วนอย่าง
ตำ่า โดยการนำาจำานวนจริงใด ๆ จำานวนเดียวกันที่หารได้ลงตัวทั้ง
จำานวนแรกและจำานวนหลังของอัตราส่วน จนกว่าจะไม่มี
จำานวนจริงใดหารได้ลงตัวแล้ว จะได้อัตราส่วนอย่างตำ่า
ขั้นที่ 2 พิจารณาอัตราส่วนที่ได้ ถ้าอัตราส่วนทั้ง
สองเป็นอัตราส่วนอย่างตำ่าที่มีจำานวนแรกและจำานวนหลังเป็น
จำานวนเดียวกัน แสดงว่าเป็นอัตราส่วนที่เท่ากัน
ตัว อย่า งที่ 3 จงตรวจสอบอัตราส่วน 2 : 10 กับ 5 : 25
และ 8 : 36 กับ 15 : 60 เท่ากันหรือไม่ โดยใช้วิธีทำาเป็น
อัตราส่วนอย่างตำ่า
♠ ..แนวทางการคิด ....จากโจทย์เขียนอัตราส่วนในรูปเศษส่วน
แล้ ว ใช้ จำา นวนเต็ ม บวกที่ ห ารลงตั ว ทั้ ง เศษแล ะส่ ว น จะได้
อัตราส่วนอย่างตำ่า พิจารณาว่าเท่ากันหรือไม่ (ดูแผนผังการคิด
ตามเส้นลูกศร)
วิธ ีท ำา 2 5 หรือ
8 15
10 กับ 25 36 กับ กับ
60

1 =1 2 1 ≠
≠ 5 5 9 4

2 5
ดัง นั้น 10= 25 ดั ง
8 15
นั้น 36  60
วิธ ีท ี่ 2 ทำา จำา นวนแรก หรือ จำา นวนหลัง ให้เ ท่า กัน
เป็นการหาจำานวนมาคูณหรือหารจำานวนแรก หรือ
จำานวนหลังแล้วนำาจำานวนที่เหลือมาเปรียบเทียบกันว่าเท่ากันหรือ
ไม่
ตัว อย่า งที่ 4 จงตรวจสอบอัตราส่วน 12 : 40 กับ 24 : 80
เท่ากันหรือไม่
♠ ..แนวทางการคิด ....จากโจทย์ใช้หลักการคูณ หรือหลักการ
หาร (ดูแผนผังการคิดตามเส้นลูกศร)

11

วิธ ีท ำา
12 24 12 24
40 กับ 80 หรือ ได้ท ำา อี80 ี
40 ก วิธ
กับ กับ

หลักการ 12 2
× 24 2 หลักการ
÷
คูณ 40 2
× เท่ากัน เท่ากัน 80 2 หาร
÷

24 12
80 40

ดัง นั้น 12 : 40 = 24 : 80

♣ ..ห ม า ย เ ห ตุ ไม่ ว่ า จะใช้ ห ลั ก การคู ณ หรื อ หลั ก การหารก็ จ ะ
เปรียบเทียบการเท่ากันของอัตราส่วนได้
วิธ ีท ี่ 3 ใช้ห ลัก การคูณ ไขว้
a : b กับ c : d เป็นอัตราส่วนสองอัตราส่วนใด ๆ ดังนั้น

a c
b d
a  d = b  c (ผลคูณไขว้)
หรือ
พจน์ไกล

a:b = c:d
พจน์ใกล้

a d = b  c (ผลคูณพจน์ไกลเท่ากับผลคูณพจน์ใกล้ )

ตัว อย่า งที่ 5 จงตรวจสอบอัตราส่วนแต่ละคู่ต่อไปนี้เท่ากันหรือ
ไม่
1.1 5 : 6 กับ 20 : 24
1.2 5 : 7 กับ 15 : 17

12

♠ ..แนวทางการคิด ....จากโจทย์..ใช้ผลคูณไขว้ หรือ ผลคูณ
พจน์ไกลพจน์ใกล้ ตรวจสอบความเท่ากัน
1.1 5 : 6 กับ 20 : 24 1.2 5 :
7 กับ 15 : 17
5 20
5 : 7 …..
6 24
15 : 17
5(24) ….. 20(6)
5(17) ….. 7(15)
120 = 120 85
≠ 105
ดัง นั้น 5 : 6 = 20 : 24 ดัง นั้น 5: 7 ≠ 15
: 17
♣ ..หมายเหตุ การเปรียบเทียบอัตราส่วนโดยการคูณไขว้
เหมาะสำาหรับอัตราส่วนที่เป็นตัวเลขน้อย ๆ หรือเป็นอัตราส่วน
อย่างตำ่า
♥..ข้อ ควรรู้..
มาตราส่ว น ก็คืออัตราส่วนที่เกี่ยวข้องกับความยาว เพี่อ
แสดงการเปรียบเทียบระหว่างระยะทางในแผนที่หรือแผนผังกับ
ระยะทางจริง ซึ่งอาจจะเป็นการย่อหรือการขยาย อาจมีหน่วย
เดียวกันหรือหน่วยต่างกันก็ได้
อัต ราทด เป็นอัตราส่วนของความเร็วรอบของล้อขับ
(เฟืองขับ) ต่อความเร็วรอบของล้อตาม (เฟืองตาม)

1.2 อัต ราส่ว นต่อ เนื่อ ง
อัตราส่วนต่อเนื่อง หรืออัตราส่วนของจำานวนหลาย
จำานวน เป็นอัตราส่วนที่แสดงการเปรียบเทียบปริมาณตั้งแต่ 3
ปริมาณขึ้นไป เขียนอยู่ในรูป a : b : c มีความหมายว่า
1.2.1 อัตราส่วนแสดงการเปรียบเทียบปริมาณสิ่งของ
กลุ่มที่หนึ่งต่อปริมาณสิ่งของกลุ่มที่สองเป็น a : b
กลุ่มที่หนึ่งต่อปริมาณสิ่งของกลุ่มที่สามเป็น a : c

13

กลุ่มที่สองต่อปริมาณสิ่งของกลุ่มที่สามเป็น b : c

หลัก การเขีย นอัต ราส่ว นต่อ เนื่อ ง
หลักการเขียนอัตราส่วนต่อเนื่อง เมื่อกำาหนดอัตราส่วน
สองอัตราส่วนหรือมากกว่าสองอัตราส่วน สามารถเขียนอัตราส่วน
ต่อเนื่องได้ดังนี้
1. ถ้า ปริม าณหลัง ของอัต ราส่ว นแรกเท่า กับ
ปริม าณแรกของอัต ราส่ว นหลัง
a : b และ b : c เมื่ออัตราส่วนทั้งสองมีค่า b เท่ากันแล้ว
สามารถเขียนอัตราส่วนต่อเนื่องได้ เช่น
a : b = 3:5
b : c = 5:7
ดัง นั้น a : b : c = 3:5:7
2. ถ้า ปริม าณหลัง ของอัต ราส่ว นแรกไม่เ ท่า กับ
ปริม าณแรกของอัต ราส่ว นหลัง ต้อ งทำา ทั้ง สองปริม าณนี้
ให้เ ท่า กัน ก่อ นจึง สามารถเขีย นอัต ราส่ว นได้
a : b และ b : c โดยที่ b ไม่เท่ากัน จะต้องทำา b ให้เท่า
กันก่อน จึงสามารถเขียนอัตราส่วนต่อเนื่องได้ เช่น
a : b = 2:3 และ b :c =
6:7
(นำา 2 คูณทั้งจำานวนหน้าและจำานวนหลัง) จะได้ a : b =
2 × 2 : 3 ×2 = 4 : 6
ดัง นั้น a : b: c = 4:6:7
ตัว อย่า งที่ 6 โจทย์ก ำา หนดอัต ราส่ว น ดัง นี้
ปริมาณที่หนึ่งต่อปริมาณที่สองเป็น 5 : 6 และปริมาณที่
สองต่อปริมาณที่สามเป็น 8 : 9
จงหาอัตราส่วนปริมาณที่หนึ่งต่อปริมาณที่สองต่อปริมาณที่สาม
วิธ ีค ิด แบบที่ 1 จากโจทย์
ปริมาณที่หนึ่ง  ปริมาณที่สอง และ ปริมาณที่
สอง  ปริมาณที่สาม
5 : 6 และ 8
: 9 ค.ร.น. =
24

14

5 ×
5 4
จากหลักการคูณจะได้ว่า 6 = 6 4 =
×
20
24
8 ×
8 3 24
และ 9 = 9 3 =
× 27
ดัง นั้น ปริม าณหนึ่ง  ปริม าณที่ส อง  ปริม าณที่
สาม = 20 : 24 : 27
วิธ ีค ิด แบบที่ 2 จากโจทย์
ปริมาณที่หนึ่ง  ปริมาณที่สอง และ ปริมาณที่
สอง  ปริมาณที่สาม
5 : 6 และ 8
: 9
วิธีนี้เราไม่ต้องหา ค.ร.น. ของ 6 และ 8 แต่ใช้
หลัก การคูณ สลับ
5 ×
5 8 40
กล่าวคือ คูณ 6 ด้วย 8 จะได้ 6 8 = × 48
8 ×
8 6 48
คูณ 9 ด้วย 6 จะได้ ×
9 6 = 54

ดัง นั้น ปริม าณหนึ่ง  ปริม าณที่ส อง  ปริม าณที่
สาม = 40 : 48 : 54
หรือ = 20 : 24 :
27
วิธ ีค ิด แบบที่ 3 จากโจทย์ ใช้ว ิธ ีล ัด (ดูแ ผนผัง การ
คูณ ตามหัว ลูก ศร)
ปริมาณหนึ่ง  ปริมาณที่สอง  ปริมาณที่สาม
5 : 6
8 : 9
40 : 48 : 54

ดัง นั้น ปริม าณที่ห นึ่ง  ปริม าณที่ส อง  ปริม าณที่
สาม = 40 : 48 : 54

15

หรือ = 20
: 24 : 27
สรุป ได้ว ่า ถ้ามีอัตราส่วนสองอัตราส่วนใด ๆ ที่แสดงการ
เปรียบเทียบปริมาณของสิ่งสามสิ่งเป็นคู่ ๆ และอัตราส่วนทีละคู่
นั้นมีปริมาณของสิ่งเดียวกันร่วมกันอยู่ สามารถเขียนอัตราส่วน
ของจำานวนทั้งสามจำานวนจากสองอัตราส่วนเหล่านั้น ด้วยการทำา
ปริมาณของสิ่งที่เป็นตัวร่วมในสองอัตราส่วนให้เป็นปริมาณที่เท่า
กัน โดยใช้หลักการหาอัตราส่วนที่เท่ากัน
ในกรณีที่มีการเปรียบเทียบ 4 ปริมาณ สามารถแสดง
การคิดคำานวณแบบวิธีลัดได้ดังนี้
ตัว อย่า งที่ 7 อัตราส่วนของอายุเป็นดังนี้ นิด  หน่อย = 2 :
3, หน่อย  น้อย = 4 : 3, โหน่ง  น้อย = 5 : 3, จง
หาอัตราส่วนอายุของนิด  โหน่ง
วิธ ีท ำา (ดูแ ผนผัง การคูณ ตามหัว ลูก ศร )
อายุนิด  อายุหน่อย  อายุน้อย  อายุโหน่ง
2 : 3
4 : 3
3 : 5
24 : 36 : 27 : 45
ดัง นั้น จากวิธ ีค ิด ลัด จะได้ว ่า อายุน ิด  อายุโ หน่ง
= 24 : 45 หรือ 8 : 15

♥..ข้อ ควรรู้..
1. ในการเปรียบเทียบปริมาณส่วนผสม ต้องเขียนหน่วย
กำากับไว้ด้วย เช่น อัตราส่วนผสมของขนมฝอยทอง แทนที่จะ
เขียนเป็นอัตราส่วนของจำานวนไข่เป็ดเป็นฟอง ต่อปริมาณนำ้าตาล
ทรายเป็นถ้วยตวง ต่อปริมาณนำ้าดอกไม้สดเป็นถ้วยตวง เป็น 4 :
1 : 2 อาจเขียนได้ว่า “อัตราส่วนของจำานวนไข่เป็ด ต่อปริมาณ
นำ้าตาลทราย ต่อปริมาณนำ้าดอกไม้สด เป็น 4 ฟอง : 1 ถ้วยตวง :
2 ถ้วยตวง

16

2. ตำาแหน่งของปริมาณส่วนผสมในอัตราส่วนต้องเป็น
ลำาดับเดียวกับลำาดับของสิ่งที่เปรียบเทียบ เช่น อัตราส่วนผสม
ของขนม ฝอยทอง
เขียนได้ ดังนี้

อัตราส่วนของไข่เป็ดเป็นฟองต่อนำ้าตาล ทรายเป็น ถ้วย
ต่อนำ้าดอกไม้สดถ้วย = 4:
1:2

1.3 โจทย์ป ัญ หาอัต ราส่ว นในงานอาชีพ และชีว ิต
ประจำา วัน
ในชีวิตประจำาวันหรือการประกอบอาชีพ จะเห็นว่ามี
อัตราส่วนเข้าไปเกี่ยวข้องกับการคำานวณค่าต่าง ๆ มากมาย เช่น
อัตราส่วนผสมการก่อสร้าง การผลิตวัสดุและครุภัณฑ์ อัตราส่วน
ผสมนำ้าผลไม้ สูตรอาหาร เป็นต้น
ตัว อย่า งที่ 8 อัตราส่วนนักเรียนชายต่อนักเรียนหญิงเท่ากับ 1
: 5 ถ้ามีนักเรียนชาย 100 คน จะมี นักเรียนหญิงกี่คน
♠ ..แนวทางการคิด ....หาจำานวนมาคูณ 1 แล้วได้ 100
โดยหาได้จากการนำา 100 ÷ 1 = 100 แล้วนำา 100 คูณทั้ง
จำานวนหน้าและจำานวนหลังของอัตราส่วน
วิธ ีท ำา อัตราส่วนนักเรียนชายต่อนักเรียนหญิง = 1 : 5
อัตราส่วนนักเรียนชายต่อนักเรียนหญิง = 1 
100 : 5  100
= 100 :
500
ดัง นั้น นัก เรีย นชาย 100 คน จะมีน ัก เรีย นหญิง
500 คน

17

ตัว อย่า งที่ 9 สี่เหลี่ยมผืนผ้ารูปหนึ่งอัตราส่วนของด้านกว้างต่อ
ด้านยาวเท่ากับ 5 : 6 ถ้าด้านยาว ยาว 30
เซนติเมตร จงหาความยาวของเส้นรอบรูป
♠ ..แนวทางการคิด ....หาจำานวนมาคูณ 6 แล้วได้ 30 โดยหา
ได้จากการนำา 30 ÷ 6 = 5 แล้วนำา 5 คูณทั้งจำานวนหน้าและ
จำานวนหลังของอัตราส่วน แล้วหาผลรวมของด้านกว้างและด้านยาว
ทั้งสี่ด้าน
วิธ ีท ำา อัตราส่วนของด้านกว้างต่อด้านยาว = 5:
6
∴ อัตราส่วนของด้านกว้างต่อด้านยาว = 5  5 :
65 = 25 : 30
ดัง นั้น ความยาวของเส้น รอบรูป = 25 + 25 +
30 + 30 = 110 เซนติเ มตร
ตัว อย่า งที่ 10 เครื่องดื่มชนิดหนึ่งมีอัตราส่วนผสม นำ้าตาลต่อ
นำ้าเท่ากับ 2 : 3 ถ้าต้องการเครื่องดื่ม ทั้งหมด 30
กิโลกรัม จะต้องใช้นำ้าตาลและนำ้าอย่างละกี่กิโลกรัม
♠ ..แนวทางการคิด ....จากโจทย์เครื่องดื่มได้จากการรวมส่วน
ผสมของนำ้าตาลกับนำ้า ดังนั้น ส่วนผสมแต่ละส่วนหาได้จาก
การนำาเครื่องดื่มทั้งหมดหารด้วยส่วนผสมทั้งหมด แล้วนำาค่าที่ได้
คูณอัตราส่วนของนำ้าตาลและนำ้า
วิธ ีท ำา อัตราส่วนนำ้าตาลต่อนำ้า = 2 : 3
เครื่องดื่ม = อัตราส่วนนำ้าตาล + นำ้า
= 2+3
= 5
∴ แบ่งเครื่องดื่ม 30 กิโลกรัม ออกเป็น 5 ส่วน
จะได้ 30 ÷ 5 = 6 อัตราส่วนนำ้าตาลต่อนำ้า =
2  6 : 3  6 = 12 : 18
ดัง นั้น จะต้อ งใช้น ำ้า ตาล 12 กิโ ลกรัม และนำ้า
18 กิโ ลกรัม
ตัว อ ย่า ง ที่ 11 ในการส่งกำา ลังด้วยสายพาน ถ้าล้อขับและล้อ
ตามหมุนด้วยความเร็วรอบ 1,000 แ ล ะ 200
รอบต่อนาที ตามลำาดับ จงหาอัตราทด

18

♠ ..แ น ว ท า ง ก า ร คิ ด ....จากโจทย์กำา หนดความเร็วรอบของล้อ
ขับและล้อตามมาให้ จึงนำามาแทนค่าเพื่อหาคำาตอบได้
วิธ ีท ำา กำาหนดให้อตราทด (i)
ั =
ความเร็วรอ
บของล้อขั1)
(Nบ
ความเร็วรอ
บของล้อตาม
(N )
2
1000
= 200
5
= 1 = 5:1
ดัง นั้น อัต ร า ท ด ข อ ง ก า ร ส่ ง กำา ลั ง ด้ ว ย ส า ย พ า น
5: 1
ตัว อ ย่า ง ที่ 12 ในการเขียนแบบชิ้ นงานจากแบบที่ กำา หนดให้
วัดความยาว H และ L ได้ 15 และ 20
มิ ล ลิเมตร จงหาความยาว H และ L ของชิ้ นงานจริ ง ค่ าใน
การเขียนแบบใช้ มาตราส่ ว น 1 : 2 กำา หนดให้ ขนาด
ขนาดในแบบ
ของชิ้นงาน = มาตราส่วน
♠ ..แนวทางการคิด ....จากโจทย์กำาหนดความยาว H และ L
มาให้ จึงนำามาแทนค่าขนาดในแบบหารด้วยมาตราส่วน เพื่อหา
คำาตอบ
1
วิธ ีท ำา การเขียนแบบใช้มาตราส่วน 1 : 2= 2
ขนาดในแบบ
ขนาดของชิ้นงาน = มาตราส่วน
15
ความยาว H = 1 = 15 
2
2 = 30 มิลลิเมตร
20
ความยาว L = 1 = 20 
2
2 = 40 มิลลิเมตร
ดัง นั้น ชิ้น งานจริง มีค วามยาว H 30
มิล ลิเ มตร
ความยาว L 40 มิล ลิเ มตร

19

ตัว อย่า งที่ 13 จงหาความลาดของหลังคา ถ้ากำาหนดให้ความ
สูงของดั้งเท่ากับ 1.6 เมตร และความลาดของหลังคาเท่ากับ 1
: 2 จงหาระยะห่างระหว่างเสา
♠ ..แ น ว ท า ง ก า ร คิ ด ....จากโจทย์ กำา หนดความสูงของดั้ง และ
ความลาดของหลังคามาให้ จึงนำามาแทนค่าหาคำาตอบ
1
วิธ ีท ำา ความลาดของหลังคา 1 : 2 = 2
กำา ห น ด ใ ห้ ค ว า ม ล า ด ข อ ง ห ลั ง ค า =
ความสูงของ
ดั้ง
1
2×ระยะห่างระ งเสา
หว่า
16
.
1
2 = 1×ระยะห่างระ งเสา
หว่า
2
ระยะห่างระหว่างเสา = 1.6 × 2 × 2 =
6.4 เมตร
ดัง นั้น ร ะ ย ะ ห่ า ง ร ะ ห ว่ า ง เ ส า เ ท่ า กั บ 6.4
เมตร

ตัว อย่า งที่ 14 ในการจัดทำานำ้าจิ้มลูกชิ้นมีส่วนผสม กระเทียม
ต่อนำ้ามะนาว เป็น 4 : 3 และนำ้ามะนาว ต่อ
พริก เป็น 2 : 3 จงเขียนอัตราส่วนกระเทียมต่อนำ้ามะนาวต่อพริก
♠ ..แนวทางการคิด ....ในการเขียนอัตราส่วน พบว่า ตัวร่วมคือ
นำ้ามะนาว ดังนั้น จะต้องทำาให้นำ้ามะนาวมีปริมาณเท่ากัน โดย
การหา ค.ร.น หรือใช้หลักการคูณสลับของตัวร่วม คือ 3, 2 จะ
ได้ 6 แล้วนำาจำานวนของตัวร่วมคูณจำานวนหน้าหรือจำานวนหลัง
ที่เหลือในอัตราส่วนทั้งสองด้วย
วิธ ีท ำา อัตราส่วนของกระเทียมต่อนำ้ามะนาว เป็น 4 : 3
อัตราส่วนของนำ้ามะนาวต่อพริก เป็น 2 : 3
จะได้ อั ต ราส่ ว นของกระเที ย มต่ อ นำ้า มะนาว เป็ น
4 2 : 3 2 = 8 : 6
อั ต ร า ส่ ว น ข อ ง นำ้า ม ะ น า ว ต่ อ พ ริ ก เ ป็ น
2 3 : 3 3 = 6 : 9

20

ดัง นั้น อั ต ร า ส่ ว น ข อ ง ก ร ะ เ ที ย ม ต่ อ นำ้า ม ะ น า ว ต่ อ
พริก 8 : 6 : 9
ตัว อย่า งที่ 15 อัตราส่วนผสมคอนกรีตประกอบด้วย หิน  ปูน
 ทราย เป็น 4 : 1 : 2 ถ้าต้องการ ผ ส ม ค อ น ก รี ต
หนัก 280 กรัม จะต้องใช้ หิน ปูน และทรายอย่างละกี่ถัง
♠ ..แนวทางการคิด ....จากโจทย์นำ้าหนักคอนกรีต ได้จากการ
รวมส่วนผสมของหิน ปูน และทราย ดังนั้นแต่ละส่วนคิดจากนำ้า
หนักคอนกรีตหารด้วยผลรวมส่วนผสม นำาผลลัพธ์ที่ได้มาหาคำา
ตอบ
วิธ ีท ำา อัตราส่วนหินต่อปูนต่อทราย = 4 : 1 : 2
คอนกรีต = อัตราส่วนหิน + ปูน + ทราย
= 4+1+2
= 7
∴ แบ่งคอนกรีต 280 กรัม ออกเป็น 7 ส่วน จะ
ได้ 280 ÷ 7 = 40 จะได้ อัตราส่วนหินต่อ
ปูนต่อทราย = 4  40 : 1  40 : 2  40
= 160 : 40 : 80

ดัง นั้น จะต้อ งใช้ห ิน 160 ถัง
ปูน 40 ถัง
ทราย 80 ถัง

ชื่อ-สกุล………………………………..แผนก
วิชา……………………...ห้อง.............เลขที่……….

แบบฝึก ทัก ษะที่ 1.1

21

1. จงเขียนอัตราส่วนแสดงการเปรียบเทียบปริมาณ 2
ปริมาณ ดังต่อไปนี้
1.1 นาย ก สูง 170 ซม. นาย ข สูง 165 ซม.
∴ อัตราส่วนความสูงของนาย ก ต่อ นาย ข =
………………………………….
1.2 พี่มีเงิน 50 บาท น้องมีเงิน 20 บาท
∴ อัตราส่วนจำานวนเงินของพี่ต่อน้อง =
…………………………………..
1.3 สับปะรด 3 ผล ราคา 33 บาท
∴ อัตราส่วนจำานวนสับปะรดต่อราคา =
……………………………………
1.4 เงาะ 3 กิโลกรัม ราคา 36 บาท
∴ อัตราส่วนจำานวนเงาะต่อราคา =
……………………………………
1.5 ทำางาน 5 วัน ต่อสัปดาห์
 อัตราส่วนเวลาทำางานต่อสัปดาห์ =
……………………………………
2. จงทำาให้อัตราส่วนต่อไปนี้ให้เป็นอัตราส่วนอย่างตำ่า
2.1 24 : 36 = ……………………
2.2 35 : 49 = ……………………
2.3 55 : 132 = ……………………
2.4 0.96 : 4.8 = ……………………
2.5 51 : 225 = ……………………
3. จงหาอัตราส่วนที่เท่ากับอัตราส่วนที่กำาหนดให้มา 3
3.1 2:3 =……………… =………………
=………………
3.2 7:8 =……………… =………………
=………………
3.3 5:6 =……………… =………………
=………………
3.4 24 : 36 =……………… =………………
=………………

22

3.5 60 : 12 =……………… =………………
=………………

4. จงตรวจสอบว่าอัตราส่วนต่อไปนี้เท่ากัน ( = ) หรือไม่ ( ≠ )
4.1 3:5 ……………….
15 : 10
4.2 40 : 32 ……………….
5:4
4.3 4.0 : 6.4 …………….…
1:4
4.4 25 เล่ม : 300 บาท ………………
5 เล่ม : 60 บาท
4.5 1 เซนติเมตร : 4,000 เมตร ………………
4,000 เมตร : 1 เซนติเมตร
5. จงเขียนอัตราส่วนต่อเนื่องต่อไปนี้
5.1 a:b = 4 : 5b : c = 5 : 6c : d =
1:2
ดังนั้น a : b : c : d = …………………………..
a: d = …………………………..
5.2 อายุของต่าย ต่ออายุของต้น เป็น 4 : 5
อายุของต้น ต่ออายุของต้อม เป็น 5 : 7
5.2.1 อัตราส่วนอายุของต่าย ต่ออายุของต้น ต่ออายุของ
ต้อม = ………………………..
5.2.2 อัตราส่วนอายุของต่าย ต่ออายุของต้อม
= ………………………..
5.3 ABCD เป็นรูปสี่เหลี่ยมรูปหนึ่งมีอัตราส่วนของความยาว
ของด้านต่าง ๆ ดังนี้
AB : BC = 4 : 3 , BC : CD = 2 : 3, AD : CD = 1 : 3
จงเขียนอัตราส่วนของความยาวของด้าน
5.3.1 AB : BC : CD =
……………………………...
5.3.2 AB : CD =
……………………………...

23

5.3.3 BC : CD : AD =
……………………………...
5.3.4 BC : AD =
……………………………...
5.3.5 AB : BC : CD : AD =
……………………………….
6. แปลนบ้านหลังหนึ่งใช้มาตราส่วน 1 : 100 ถ้าความยาว
ของห้องหนึ่งบนแปลนยาว 8.5 เซนติเมตร ความยาวจริงมี
ค่าเท่าใด
………………………………………………………………
………………………………….
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
...............................................................................
7. ในการผสมคอนกรีต จะใช้อัตราส่วนปูน ต่อ กรวด ต่อ ทราย
เป็น 4 : 1 : 3 ถ้าผสมทั้ งสามอย่ าง แล้ ว ได้ ค อนกรี ต หนั ก
720 ตัน จะต้องใช้ปูน กรวด และ ทรายอย่างละกี่ตัน
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..

24

………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
8. ในการทำาแชมพูสมุนไพร ประกอบด้วยส่วนผสม อัตราส่วน
ปริมาณหัวแชมพูต่อปริมาณ
ผงข้นต่อปริมาณลาโนลีนต่อปริมาณผงฟองต่อปริมาณนำ้า
มะกรูดต่อปริมาณว่านหางจระเข้
ต่อปริมาณนำ้าสะอาด เท่ากับ 20 : 4 : 2 : 6 : 3 :
10 : 25 ถ้าใช้ลาโนลีน 100 กรัม
จะได้ปริมาณแชมพูสมุนไพรทั้งหมดเท่าไร
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..

9. ในการปลูกพืชโครงการเศรษฐกิจพอเพียงของหมู่บ้านแห่ง
หนึ่ง มีพื้นที่ปลูกข้าวต่อพื้นที่ปลูกข้าวโพด เท่ากับ 3 : 2

25

และมีพื้นที่ปลูกข้าวโพดต่อพื้นที่ปลูกถั่วเหลือง เท่ากับ 7 : 4
ถ้าเขาปลูกข้าว 42 ไร่ พื้นที่ปลูกพืชทั้งหมดเป็นเท่าไร
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
10. เหล็กเส้นยาว 30 เมตร แบ่งออกเป็น 3 ส่วน โดยมี
อัตราส่วนความยาวของเหล็กเส้นทั้งสาม เท่ากับ 4 : 5 : 6
จงหาความยาวของเหล็กเส้นทั้งสามเส้น
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
...............................................................................
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..
………………………………………………………………
…………………………………..

26

2. สัด ส่ว น (Proportion)
ความหมายของสัด ส่ว น
สัด ส่ว น คือ อัตราส่วนสองอัตราส่วนที่เท่ากัน เช่น
4= 40
หรือ 4 : 9 = 40 :
9 90
90
12 36
= หรือ 12 :13 = 36 :
13 39
39
2.1 สมบัต ิข องสัด ส่ว น
a c
ถ้า a : b = c : d หรือ =
b d

ad = bc (ผลคูณของพจน์
กลางเท่ากับผลคูณของพจน์ท้าย)
โดยที่ a , b , c และ d ไม่เท่ากับศูนย์
♥..ข้อ ควรรู้..เราใช้สมบัติของสัดส่วนและการแก้สมการในการ
หาค่าตัวแปรที่อยู่ในสัดส่วน
ตัว อย่า งที่ 1 จงหาค่า m ในสัดส่วน 8 : 11 = m : 33
8 :11 = m : 33

8(33) = m(11)
8(33)
11 = m
24 = m
ดัง นั้น m = 24
ตัว อย่า งที่ 2 จงหาค่า m ในสัดส่วน (m – 4) : 81 = 7 :
9

27

(m – 4) : 81 = 7:9

9(m – 4) = 7(81)
7(81)
m–4 =
9
m–4 = 63
m = 63 + 4 = 67
ดัง นั้น m = 67
ตัว อย่า งที่ 3 จงหาค่า m ในสัดส่วน (m – 3) : 7 = (m
+ 1) : 5
(m – 3) : 7 = (m + 1) : 5
5(m – 3) = 7(m + 1)
5m – 15 = 7m + 7
5m – 7m = 7 + 15
– 2m = 22
22
m = = – 11
−2
ดัง นั้น m = – 11

2.2 ชนิด ของสัด ส่ว น
สัดส่วน เป็นการกล่าวถึงอัตราส่วนที่เท่ากันสองอัตราส่วน
ซึ่งสัดส่วนแบ่งเป็น 2 ชนิด
ดังนี้ คือ
2.2.1 สัด ส่ว นตรง หมายถึง สัดส่วนที่แสดงการเปรียบ
เทียบอัตราส่วนสองอัตราส่วน ที่มีความสัมพันธ์ไปในทาง
เดียวกัน โดยที่อัตราส่วนหนึ่งเพิ่มขึ้น อีกอัตราส่วนหนึ่งก็จะเพิ่ม
ตาม
หรือ อัตราส่วนหนึ่งลดลง อีกอัตราส่วนหนึ่งก็จะลดลงตาม เช่น
ก๋วยเตี๋ยว 1 ชาม ราคา 20 บาท

28

ความสัมพันธ์ของจำานวนชามก๋วยเตี๋ยวกับราคาไปในทาง
เดียวกัน กล่าวคือ เมื่อจำานวนชามก๋วยเตี๋ยวเพิ่มขึ้นราคาจะเพิ่ม
ขึ้นตาม ถ้าจำานวนชามก๋วยเตี๋ยวลดลงราคาจะลดลงตามไปด้วย
ความสัมพันธ์ดังกล่าว เขียนเป็นสัดส่วนตรงได้ดังนี้
จำานวนชาม
4= 6 1= 1
80120 2020
ราคา
2= 1
4020
1= 1
2020
สมบัต ิข องสัด ส่ว นตรง
a : b และ c : d เป็นสัดส่วนตรงก็ต่อเมื่อ
a= c
a : b = c : d หรือ หรือ ad =
b d
bc
โดยที่ a , b , c และ d ต้องไม่เท่ากับศูนย์
ตัว อย่า งที่ 4 กำาหนดให้ a : b เป็นสัดส่วนตรงกับ c : d
1) เมื่อ a = 4 , b = 7 , c = 8 , d จะมีค่าเท่าไร
2) เมื่อ a = 20 , b = 30 , d = 6 , c จะมีค่า
เท่าไร
3) เมื่อ a = 13 , c = 39 , d = 45 , b จะมีค่า
เท่าไร
4) เมื่อ b = 130 , c = 13 , d = 10 , a จะมีค่า
เท่าไร
เนื่องจาก a : b = c : d เป็นสัดส่วนตรง จะได้
a:b = c:d

29

ad = bc

1) 4 : 7 = 8:d
4(d) = 8(7)
8(7)
d =
4 = 14
ดัง นั้น d = 14
2) 20 : 30 = c:6
(30)c = 20(6)
20(6)
c =
30
c = 4
ดัง นั้น c = 4

3) 13 : b = 39 : 45
39(b) = 13(45)
13(45)
b =
39
b = 15
ดัง นั้น b = 15

4) a : 130 = 13 : 10
(10)a = 13(130)

13(130)
a =
10 = 169
ดัง นั้น a = 169
2.2.2 สัด ส่ว นผกผัน หมายถึง สัดส่วนที่แสดงการเปรียบเทียบ
อัตราส่วนสองอัตราส่วน ที่มีความสัมพันธ์ไปในทางตรงกันข้าม

30

โดยที่อตราส่วนหนึ่งเพิ่มขึ้น อีกอัตราส่วนหนึ่งจะลดลง หรือ
ั
อัตราส่วนหนึ่งลดลง อีกอัตราส่วนหนึ่งจะเพิ่มขึ้น เช่น
ช่างก่อสร้าง 10 คน เทพื้นปูนเสร็จภายในเวลา 4 วัน
ช่างก่อสร้าง 20 คน เทพื้นปูนแบบเดียวกันเสร็จภายใน
เวลา 2 วัน
ช่างก่อสร้าง 5 คน เทพื้นปูนแบบเดียวกันเสร็จภายใน
เวลา 8 วัน
ความสัมพันธ์ของจำานวนคนกับเวลาที่ใช้ทำางานไปในทางตรง
กันข้าม กล่าวคือ เมื่อจำานวนคนเพิ่มขึ้นจำานวนวันทำางานลดลง ถ้า
จำานวนคนลดลงจำานวนวันทำางานเพิ่มขึ้น ความสัมพันธ์ดังกล่าวเขียน
เป็นสัดส่วนผกผันได้ดังนี้

จำานวนคน
1020
=
5=5
2 4 11
จำานวนวัน
สมบัต ิข องสัด ส่ว นผกผัน
a : b และ c : d เป็นสัดส่วนผกผันก็ต่อเมื่อ
a= d
หรือ
a:c = d:b
c b หรือ ab = cd
โดยที่ a , b , c และ d ต้องไม่เท่ากับศูนย์
ตัว อย่า งที่ 5 กำาหนดให้ a : b เป็นสัดส่วนผกผันกับ c : d
1) เมื่อ a = 4 , b = 27 , c = 9 , d จะมีค่าเท่าไร
2) เมื่อ a = 25 , b = 6 , d = 5 , c จะมีค่าเท่าไร
3) เมื่อ a = 121 , c = 99 , d = 11 , b จะมีค่า
เท่าไร
เนื่องจาก a : b และ c : d เป็นสัดส่วนผกผัน จะได้
a:c = d:b
ab = cd
1) a : c = d : b 4(27) =
d(9)
4 : 9 = d : 27

31

4(27) ดัง นั้น c = 30
9 = d
3) a : c = d:b
12 = d
ดัง นั้น d = 12 121 : 99 = 11 : b

2) a : c = d:b 121(b) = 11(99)
b =
25 : c = 5:6
11(99)
25(6) = 5(c) 121
25(6)
5 = c ดัง นั้น b = 9
30 = c

32

2.3 โจทย์ป ัญ หาสัด ส่ว นในงานอาชีพ และชีว ิต ประจำา วัน
การแก้โจทย์ปัญหาเกี่ยวกับสัดส่วน มีหลักการดังนี้
1) สมมติตัวแปรแทนจำานวนที่ต้องการหา
2) เขียนสัดส่วนแสดงการเท่ากันของอัตราส่วนที่กำาหนด
ให้สองอัตราส่วน โดยให้ลำาดับของสิ่งที่เปรียบเทียบกันในแต่ละ
อัตราส่วนเป็นลำาดับเดียวกัน
3) หาค่าตัวแปรที่ต้องการ โดยใช้สมบัติของสัดส่วน
ตัว อย่า งที่ 6 นมเย็น อัตราส่วนนมต่อนำ้าแดงเท่ากับ 2 : 1 ถ้า
ใช้นำ้าแดง 15 ลิตร จะต้องใช้นมกี่ลิตร
วิธ ีท ำา สมมติให้ y แทนปริมาณนมที่ต้องใช้
นม : นำ้าแดง = 2 : 1
y : 15 = 2:1
(1)y = 2(15)
2(15)
y =
1 = 30
ดัง นั้น ถ้า ใช้น ำ้า แดง 15 ลิต ร จะต้อ งใช้น ม
30 ลิต ร
ตัว อย่า งที่ 7 หมู 60 ตัว กินอาหารจำานวนหนึ่งหมดภายใน
เวลา 30 วัน ถ้าต้องการให้อาหารนี้หมด ภายในเวลา
10 วัน จะต้องเลี้ยงหมูกี่ตัว
วิธ ีท ำา จะเห็นได้ว่า ถ้าจำานวนหมูเพิ่มมากขึ้น จำานวนวันที่กิน
อาหารจะลดลง
ดังนั้น สัดส่วนจำานวนหมูต่อจำานวนวันที่กินอาหาร เป็น
สัดส่วนผกผัน
สมมติให้ p แทนจำานวนหมูที่จะกินอาหารหมดภายในเวลา
10 วัน
อัตราส่วนจำานวนหมูต่อจำานวนวันที่กินอาหารเป็น 60 :
30 และ p : 10
เนื่องจากเป็นสัดส่วนผกผัน จะได้
60 : p = 10 : 30
10(p) = 60(30)

33

60(30)
p =
10
p = 180
ดัง นั้น ถ้า ต้อ งการให้อ าหารนี้ห มดภายในเวลา 10 วัน
จะต้อ งเลี้ย งหมู 180 ตัว
ตัว อย่า งที่ 8 โจ๊กขับรถจักรยานยนต์ด้วยความเร็ว 60
กิโลเมตร/ชั่วโมง ใช้เวลาเดินทางจากบ้านถึง
วิทยาลัยฯ 30 นาที ถ้าต้องการใช้เวลาเดินทาง 20 นาที
จะต้องขับรถด้วยความเร็วเท่าไร
วิธ ีท ำา จะเห็นได้ว่า ถ้าความเร็วของรถจักรยานยนต์เพิ่มขึ้น
เวลาที่ใช้ในการเดินทางจะลดลง
ดังนั้น สัดส่วนความเร็วของรถจักรยานยนต์ต่อเวลาใน
การเดินทาง เป็นสัดส่วนผกผัน
สมมติให้ v แทนความเร็วของรถจักรยานยนต์ที่ทำาให้เวลา
เดินทางเหลือ 20 นาที
อัตราส่วนความเร็วต่อเวลาที่ใช้ในการเดินทางเป็น 60 :
30 และ v : 20
เนื่องจากเป็นสัดส่วนผกผัน จะได้
60 : v = 20 : 30
20(v) ) = 60(30)
60(30)
v=
20
v = 90
ดัง นั้น ถ้า ต้อ งการใช้เ วลาเดิน ทาง 20 นาที จะต้อ ง
ขับ รถจัก รยานยนต์ด ้ว ยความเร็ว
90 กิโ ลเมตร/ชั่ว โมง

34

วิชา……………………...ห้อง.............เลขที่……….

1. จงเขียนสัดส่วนทั้ง 2 แบบ พร้อมเติมตัวเลขทีหายไปให้สมบูรณ์
่
1 4
ตัว อย่า ง 1 : 2 = 4 :8 หรือ 2 = 8
1.1 10 : 3 = : 9 หรือ ..……………………..
1.2 3 : 4 = 6 : หรือ ………………………
1.3 : 3 = 6 : 9 หรือ ………………………
1.4 : 17 = 42 : 119 หรือ ………………………
1.5 45 : 51 = 15 : หรือ……………………….
2. จงหาค่าของตัวแปรในสัดส่วนต่อไปนี้
24 8
2.1 30= c
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………

35

a 49
2.2 5 = 35
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………

(b 1
+) 12
2.3 9
= 27
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
5 48
2.4 x 3 = 108
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
x 8
+ 64
2.5 9 = 72

36

……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
…………………………………
a d
3. กำาหนดให้ a, b, c และ d เป็นสัดส่วนผกผัน และ b = c
จงหา
3.1 ค่าของ a เมื่อ b = 7, c = 49, d =
21
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
…………………………………
3.2 ค่าของ c เมื่อ a = 3, b = 4, d = 10
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
3.3 ค่าของ d เมื่อ a = 0.5, b = 0.8, c = 5.6
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………

37

……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
3.4 ค่าของ b เมื่อ a = 5.2, c = 1.6, d = 1.3
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
3.5 ค่าของ d เมื่อ a = 0.5 , b = 2 , c = 8
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………

4. อัตราส่วนของจำานวนผู้ที่ได้ทำางานต่อจำานวนผู้สมัครงานเป็น 2 :
7 ถ้ามีผู้สมัครงาน 910 คน จะมี
ผู้ที่ได้ทำางานกี่คน
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………

38

……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
…………………………………
5. ห้องเรียนห้องหนึ่งมีนักเรียนชาย 4 คน ต่อนักเรียนหญิง 3 คน
ถ้านักเรียนห้องนี้ มีทั้งหมด
35 คน จะมีนักเรียนชายและนักเรียนหญิงกี่คน
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
…………………………………
6. ในการทำางานชิ้นหนึ่งจะใช้จำานวนคนงานชาย 10 คน จะ
ทำางานชิ้นนั้นเสร็จในเวลา 28 วัน จงหาว่า ถ้าใช้คนงานชาย 35
คน จะทำางานชิ้นนั้นเสร็จในเวลากี่วัน
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
…………………………………

39

7. เรือลำาหนึ่งมีอาหารพอกินสำาหรับ 150 คน ได้นาน 7 วัน ถ้ามีคน
เพียง 70 คน จะกินอาหารได้
นานกี่วัน
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
8. ขับรถยนต์ไปจังหวัดหนึ่งด้วยความเร็ว 60 กิโลเมตรต่อชั่วโมง
ใช้เวลาเดินทาง 3 ชั่วโมงครึ่ง
ถ้ า ต้ อ งการใช้ เ วลาเดิ น ทาง 2 ชั่ ว โมง จะต้ อ งใช้ ค วามเร็ ว
เท่าไร
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………

40

……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………
……………………………………………………………………

3. ร้อ ยละ (Percent)
ความหมายของร้อ ยละ
ร้อ ยละหรือ เปอร์เ ซ็น ต์ คือ อัตราส่วนของจำานวนใด
จำานวนหนึ่งต่อ 100 เขียนแทนด้วย
a
a : 100 หรือเขียนเป็นเศษส่วนได้
100 อเขียนในรูป
หรื
สัญลักษณ์ “ร้อ ยละ a” หรือ “a %” เช่น
3 : 100 เขียนแทนด้วย ร้อยละ 3 หรือ 3 %
13
เขียนแทนด้วย ร้อยละ 13 หรือ 13
100
%
0.05
เขียนแทนด้วย ร้อยละ 0.05 หรือ
100
0.05 %
42: 100 เขียนแทนด้วย ร้อยละ 42 หรือ
5 5
42 %
5
การเขีย นอัต ราส่ว นให้อ ยู่ใ นรูป ร้อ ยละ
1) ใช้หลักการคูณเพื่อทำาตัวส่วนให้เป็น 100
2) ใช้ความรู้เรื่อง สัดส่วน ในการหาคำาตอบ
ตัว อย่า งที่ 1 จงเขียนอัตราส่วนแต่ละข้อต่อไปนี้ให้อยู่ในรูปร้อย
ละ

41

1) 4 : 25
2) 17 : 50
5
3)
7
4) 9 : 11
5) 0.02 : 10
วิธ ีท ี่ 1 วิธ ีท ี่ 2
1) 4 : 25 = 4  4 : 1) 4 : 25 = m : 100
25  4 4(100) = m(25)
= 16 : 100
= 16 % 4(100)
25 = m
16 = m
4 : 25 = 16 : 100
= 16 %

2) 17 : 50 = 17  2 2) 17 : 50 = m : 100
: 50 2 17(100) = m(50)
= 34 : 100
= 34 % 17(100)
50 = m
34 = m
17 : 50 = 34 : 100
= 34 %

3) 5 : 7 = 5 3) 5:7 = m:
100 : 7  100 100
= 500 : 5(100) =
700 m(7)
= 500 ÷
7 : 700 ÷ 7
5(100)
= m
7

42

= 71.43 :
100 71.43 = m
= 71.43 % 5:7 =
71.43 : 100
=
71.43 %
4) 9 : 11 = 9  4) 9 : 11 = m:
100 : 11  100 100
= 900 : 9(100) =
1,100 m(11)
= 900 ÷ 11
: 1,100 ÷ 11
9(100)
= 81.82 :
11 = m
100
81.82 = m
= 81.82 %
9 : 11 =
81.82 : 100
=
81.82 %

5) 0.02 : 10 = 5) 0.02 : 10 = m
0.02  10 : 10  10 : 100
= 0.2 : 0.02(100) =
100 m(10)
= 0.2 %
0.02(100)
=
10
m

0.2 =
m

43

0.02 : 10 =
0.2 : 100
=
0.2 %
การเขียนอัตราส่วนให้เป็นร้อยละในบางครั้ง ใช้หลักการหาร
เพื่อทำาตัวส่วนให้เป็น 100
ได้ดังตัวอย่างต่อไปนี้
ตัว อย่า งที่ 2 จงเขียนอัตราส่วนแต่ละข้อต่อไปนี้ให้อยู่ในรูปร้อย
ละ
60 500
1) 2) 1,000 3)
200
0.005
10,000
60 0.005
1)
200 = 3) 10,000
=
60 2
÷ 0.005
÷100
200
÷2 10,000
÷100

30 =
=
100 0.00005
= 30 %
100
=
500 0.00005 %
2) 1,000
=
500÷10
1,000
÷10

50
=
100
= 50 %

44

การเขีย นร้อ ยละให้อ ยู่ใ นรูป อัต ราส่ว น
ร้อยละ a หรือ a % เขียนในรูปอัตราส่วนได้ a : 100
a
หรือ
100
ตัว อย่า งที่ 3 จงเขียนร้อยละแต่ละข้อต่อไปนี้ให้อยู่ในรูป
1) ร้อยละ 13 2) 12.5 % 3) 72%
9
3
10
4) ร้อยละ 0.05 5) ร้อยละ 6)
5
41%
2

13
1) ร้อยละ 13 =
3) 72% =
9
100 65
%
=
9
13 : 100 65 100
÷
=
9
2) 12.5 % =
12.5 65 1
×
=
100 9 100
= 65 5
÷
= 9005
÷
12.5
×10
100
×10 13
=
180
=
125 = 13 : 180
1,000
4) ร้อยละ 0.05 = 0.05
= : 100
125÷125 1 =
1,000
÷125 =
8 0.05100 : 100100
= 1: 8

45

= 5: 53
=
10,000 500
= 5÷5: = 53 : 500
10,000 ÷ 5
= 1 : 2,000 6) 41% = 9%
2 2
3 3 9
ร้อยละ 10 = 10 : = ÷ 100
5)
5 5 2
100 9× 1
=
53 100 2 100
= ÷
5 9
=
53 1 200
= ×
5 100 = 9 : 200
3.1 การคำา นวณเกี่ย วกับ ร้อ ยละ
การคำา นวณเกี่ยวกับร้อยละ ทำา ได้โดยการนำา ความรู้เรื่อง
สัดส่วนมาใช้โดยที่มีจำา นวนหนึ่งเป็น 100 เสมอ ซึ่งเขียนอยู่ใน
a c
รูป b = 100 ดังนั้นในการคำานวณจึงเกี่ยวข้องกับค่าเพียง 3 ค่า
คือ
a , b และ c ดังนั้น ก่อนที่จะแก้โจทย์ปัญหาร้อยละ ควรฝึกการ
คำา นวณเกี่ ย วกั บ ร้ อ ยละในกรณี ต่ า ง ๆ กั น โดยใช้ สั ด ส่ ว นซึ่ ง
เกี่ยวข้องกับจำานวนหนึ่งที่เป็น 100 และเขียนให้อยู่ในรูปสัดส่วน
ได้ดังนี้
a : b = c : 100
c ×b
a =
100
a = c % ของ b
ตัว อย่า งที่ 4 จงหาผลลัพธ์แต่ละข้อต่อไปนี้
4
10 %
1) 30 % ของ 900 มีค่าเท่าใด 3)
5
ของ 2,000 มีค่าเท่าใด
2) 5.5 % ของ 10,000 มีค่าเท่าใด 4)
0.5 % ของ 1,000,000 มีค่าเท่าใด

46

วิธ ีท ำา 1) 30 % ของ 900 มีค่าเท่าใด หรือ
หาได้จาก
เขียนเป็นสัดส่วนได้ดังนี้ a = c%
ของ b
30 : 100 = a : 900 a =
30 % ของ 900
30(900) = a(100) a =
30 %  900
30(900)
100 = a a =
30 900
×
100
270 = a a = 270
ดัง นั้น 30 % ของ 900 มีค ่า เท่า กับ 270
ดัง นั้น 30 % ของ 900 มีค ่า เท่า กับ 270
2) 5.5 % ของ 10,000 มีค่าเท่าใด หรือ หาได้
จาก
ของ b
5.5 : 100 = a : 10,000 a
= 5.5 % ของ 10,000
5.5(10,000) = a(100) a =
5.510,000
×
100
5.5(10,000
)
= a a
100
= 550
550 = a ดัง นั้น
5.5 % ของ 10,000 มีค ่า เท่า กับ 550 ดัง นั้น 5.5
% ของ 10,000 มีค ่า เท่า กับ 550
4
10 % ของ 2,000 มีค่าเท่าใด
3) หรือ
5

47

เขียนเป็นสัดส่วนได้ดังนี้ a = c
% ของ b
4
10 : 100 = a : 2,000 a =
5
4
10 % ของ 2,000
5
54 100
÷ = a : 2,000 a =
5
4
10 %× 2,000
5
54 1
×
5 100 a : 2,000
= a =
54 2,000
%×
5
54
500= a : 2,000 a
 54 
=  ÷ 100 2,000
×
 5 

54 : 500 = a : 2,000 a
 54 1 
=  ×  × 2,000
 5 100
54(2,000) = a(500) a =
54 2,000
×
500
54(2,000)
500 = a a =
216
216 = a
4
10% ของ 2,000 มีค ่า เท่า กับ 216
ดัง นั้น
5
4
ดัง นั้น 10% ของ 2,000 มีค ่า เท่า กับ 216
5

48

4) 0.5 % ของ 1,000,000 มีค่าเท่าใด หรือ
ของ b

0.5 : 100 = a : 1,000,000
a = 0.5 % ของ 1,000,000

0.5(1,000,000) = a(100) a
0.51,000,000
×
=
100
0.5(1,000,
000)
= a a
100
= 5,000
5,000 = a ดัง นั้น
0.5 % ของ 1000,000 มีค ่า เท่า กับ 5,000
ดัง นั้น 0.5 % ของ 1,000,000 มีค ่า เท่า กับ 5,000

1) 50 คิดเป็นกี่เปอร์เซ็นต์ของ 500
2) 200 คิดเป็นกี่เปอร์เซ็นต์ของ 2,000
3) 400 คิดเป็น 30 % ของจำานวนใด
1) 50 คิดเป็นกี่เปอร์เซ็นต์ของ 500 หรือ หาจาก
ของ b
50 : 500 = c : 100 50
= c % ของ 500
50(100) = c(500) 50
= c %  500

49

50(100)
500 = c 50 =
c × 500
100
10 = c 50
= c(5)
ดัง นั้น 50 คิด เป็น 10 % ของ 500
50
5= c
10 = c
ดัง นั้น 50 คิด เป็น
10 % ของ 500
2) 200 คิดเป็นกี่เปอร์เซ็นต์ของ 2,000 หรือ
หาจาก
ของ b
200 : 2,000 = c : 100 200
= c % ของ 2,000
200(100) = c(2,000)
200 = c %  2,000
200(100)
2,000 = c 200
c × 2,000
=
100
10 = c 200
= c(20)
ดัง นั้น 200 คิด เป็น 10 % ของ 2,000
200
20 = c
10 = c
10 % ของ 2,000

50

3) 400 คิดเป็น 25 % ของจำานวนใด หรือ หาจาก
ของ b

400 : b = 25 : 100 400
= 25 % ของ b

400(100) = 25(b) 400
= 25 %  b
400(100)
25 = b
25 b
×
400 =
100
1,600 = b 400
1× b
=
4
ดัง นั้น 400 คิด เป็น 25 % ของ 1,600
400(4) = b
1,600 = b
25 % ของ 1,600
1) 10 % ของ 15 % ของ 200,000 มีค่าเท่าใด
2) 20 % ของ 10 % ของ 5 % ของ 1,000,000
มีค่าเท่าใด
3) 100 % – (10 %20 %) มีค่าเท่าใด
4) 100 % – (60 %  70 %) มีค่าเท่าใด
1) 10 % ของ 15 % ของ 200,000 = 10 %  15 %
 200,000
10 15 200,000
× ×
=
100100
= 3,000

51

2) 20 % ของ 10 % ของ 5 % ของ 1,000,000 =
20 %  10 %  5 %  1,000,000
=
20 10 5 ×1,000,000
× ×
100100100
= 1,000

100 10 20
− × 
3) 100 % – (10 % 20 %) = 
100 100100


= 1 – (0.10  0.20)
= 1 – 0.02
= 0.98 = 98 %
100 60 70
− × 
4) 100 % – (60 %  70 %) = 
100 100100


= 1 – (0.6  0.7)
= 1 – 0.42
= 0.58 =
58 %

3.2 โจทย์ป ัญ หาร้อ ยละในงานอาชีพ และชีว ิต ประจำา
วัน
การแก้โจทย์ปัญหาเกี่ยวกับร้อยละมีขั้นตอน ดังนี้
3.2.1กำาหนดตัวแปรแทนสิ่งที่โจทย์ต้องการ
3.2.2 เขียนร้อยละให้อยู่ในรูปของสัดส่วนแสดง
อัตราส่วนที่เท่ากันจากโจทย์ที่กำาหนดให้และสิ่งที่โจทย์ต้องการหา
3.2.3 หาจำานวนแทนตัวแปรในสัดส่วน โดยใช้
สมบัติของสัดส่วนและการแก้สมการในการหาค่าตัวแปรที่อยู่ใน
สัดส่วน
ตัว อย่า งที่ 7 สุทธิภัทรสอบวิชาคณิตศาสตร์ประยุกต์ 1 ได้
คะแนน 17 คะแนน จากคะแนนเต็ม

52

20 คะแนน จงหาว่าคะแนนที่สุทธิภัทรสอบได้คิด
เป็นกี่เปอร์เซ็นต์ของคะแนนเต็ม
วิธ ีท ำา สมมติให้ สุทธิภัทรสอบได้ m %
หมายความว่า คะแนนเต็ม 100 คะแนน
สุทธิภัทร สอบได้คะแนน m คะแนน
เขียนเป็นสัดส่วนได้ดังนี้
คะแนนที่สอบได้  คะแนนเต็ม = 17 : 20
m : 100
= 17 : 20
m(20) =
17(100)

17(100)
m =
20
m
= 85
ดัง นั้น คะแนนที่ส ุท ธิภ ัท รสอบได้ค ิด เป็น 85 % ของ
คะแนนเต็ม
ตัว อย่า งที่ 8 วิชาคณิตศาสตร์ประยุกต์ 1 เรียน 2 ชั่วโมง
ต่อสัปดาห์ 1 ภาคเรียน เรียน 18 สัปดาห์
นักเรียนต้องมีเวลาเรียนไม่น้อยกว่า 80 %
ของเวลาเรียนทั้งหมด จึงจะมีสิทธิ์เข้า
ประเมินผลสรุปผลการเรียนปลายภาค จงหา
ว่านักเรียนต้องเรียนกี่ชั่วโมง จึงจะมีสิทธิ์
เข้าประเมินผลสรุปผลการเรียนปลายภาคและ
ขาดเรียนได้กี่ชั่วโมง
เรียน 2 ชั่วโมงต่อสัปดาห์ 1 ภาคเรียน เรียน 18
สัปดาห์
จำานวนชั่วโมงเรียนทั้งหมด = 2 18
= 36 ชั่วโมง

53

มีเวลาเรียน 80 % ของเวลาเรียนทั้งหมด
หมายความว่า จำานวนชั่วโมงเรียนทั้งหมด 100
ชั่วโมง เข้าเรียน 80 ชั่วโมง
สมมติให้ m แทนจำานวนชั่วโมงที่เข้าเรียน
จำานวนชั่วโมงที่เข้าเรียน  จำานวนชั่วโมงเรียน
ทั้งหมด = 80 : 100

m : 36 = 80 : 100

m(100) = 80(36)

80(36)
m =
100

m = 28.8 ≈ 29
ดัง นั้น นัก เรีย นจะต้อ งเข้า เรีย นไม่น ้อ ยกว่า 29
ชั่ว โมง
นัก เรีย นขาดเรีย นได้ = 36 – 29 = 7
ตัว อย่า งที่ 9 นักเรียนระดับชั้น ปวช.1 ทำาโครงการหาราย
ได้ระหว่างเรียนโดยการไปซื้อเสื้อผ้า
มาจำาหน่าย โดยทางร้านให้ส่วนลด 25 %
จากยอดซื้อ ถ้านักเรียนมียอดซื้อ
2,000 บาท อยากทราบว่านักเรียนจะได้รับ
ส่วนลดเท่าใด และต้องชำาระเงิน
ให้กับทางร้านเท่าใด
ส่วนลด 25 % หมายความว่า ยอดซือ 100 บาท
้
ได้รับส่วนลด 25 บาท
สมมติให้ m แทนส่วนลดที่ได้รับ

54

ส่วนลด  ยอดซื้อ = 25 : 100
m : 2,000 = 25 :
100
m(100) = 25(2,000)
25(2,000)
m =
100
m = 500
ดัง นั้น นัก เรีย นจะได้ร ับ ส่ว นลด 500 บาท
และต้อ งชำา ระเงิน ให้ท างร้า น = 2,000 –
500 = 1,500 บาท
ตัว อย่า งที่ 10 ซือเสื้อแขนสั้น 20 ตัว ๆ ละ 60 บาท ถ้า
้
ต้องการกำาไร 30 %
จะต้องขายเสื้อราคาตัวละเท่าใด
สมมติให้ เสื้อราคาขายตัวละ m บาท
กำาไร 30 % หมายความว่า ราคาทุน 100 บาท
ได้กำาไร 30 บาท
ราคาขาย = ราคาทุน + กำาไร = 100 + 30
= 130
ราคาขาย  ราคาทุน = 130 : 100
m : 60 = 130 : 100
m(100) = 130(60)
130(60)
m =
100
m = 78
ดัง นั้น ถ้า ต้อ งการกำา ไร 30 % ต้อ งขายเสื้อ ตัว ละ
78 บาท

55

ตัว อย่า งที่ 11 นิดหน่อยได้รับเงินเดือน ๆ ละ 7,000 บาท
จ่ายเป็นค่าอาหาร 60 % และค่าใช้จ่าย
ส่วนตัว 25 % อยากทราบว่า นิดหน่อย
เหลือเงินเดือน ๆ ละเท่าใด
ค่าอาหาร 60 % หมายความว่า เงินเดือน 100
บาท เป็นค่าอาหาร 60 บาท
ค่าอาหาร = 60 %  7,000
60 7,000
×
=
100
= 4,200
ค่าใช้จ่ายส่วนตัว 25 % หมายความว่า เงินเดือน
100 บาท เป็นค่าใช้จ่ายส่วนตัว 25 บาท
ค่าใช้จ่ายส่วนตัว = 25 %  7,000
25 7,000
×
= = 1,750
100
ค่าใช้จ่ายทั้งหมด = 4,200 + 1,750 =
5,950
ดัง นั้น นิด หน่อ ยเหลือ เงิน เดือ น ๆ ละ = 7,000 –
5,950 = 1,050 บาท
ตัว อย่า งที่ 12 เมื่อปีที่แล้ว เจ้ยซื้อผ้าราคาเมตรละ 120
บาท ในปีนี้ราคาผ้าเพิ่มขึ้นเป็นเมตรละ
150 บาท จงหาว่าราคาผ้าเพิ่มขึ้นคิดเป็นกี่
เปอร์เซ็นต์ของราคาเดิม
การคิดเปอร์เซ็นต์ของการขึ้นราคาหรือลดราคา ให้
คิดเทียบกับราคาเดิมเสมอ
ผ้า 1 เมตร ราคาเพิ่มขึ้น = 150 – 120 =
30 บาท
อัตราส่วนราคาที่เพิ่มขึ้นต่อราคาเดิม = 30 :
120

56

สมมติให้ p แทนราคาที่เพิ่มขึ้น เมื่อราคาเดิมเป็น
100 บาท
อัตราส่วนราคาที่เพิ่มขึ้นต่อราคาเดิม = p :
100
ราคาที่เพิ่มขึ้น  ราคาเดิม = 30 : 120

p : 100 = 30 :
120
p(120) =
30(100)
p =
30(100)
120 = 25
ดัง นั้น ราคาผ้า เพิ่ม ขึ้น เมตรละ 25 % ของ
ราคาเดิม
ตัว อย่า งที่ 13 วิทยาลัยเทคนิคเพชรบูรณ์ปลูกต้นไม้ยืนต้น
ตามแนวรั้วจำานวน 1,500 ต้น โดยมีต้นมะพร้าว
จำานวน 40 ต้น อยากทราบว่าต้นมะพร้าวคิดเป็นกี่
เปอร์เซ็นต์ของต้นไม้
ยืนต้นทั้งหมด
ต้นมะพร้าวคิดเป็น p % ของต้นไม้ยืนต้นทั้งหมด
หมายความว่า ต้นไม้ยืนต้นทั้งหมด 100 ต้น มีต้น
มะพร้าว p ต้น
ต้นมะพร้าว  ต้นไม้ยืนต้นทั้งหมด = 40 :
1,500
p:
100 = 40 : 1,500
p(1,500) =
40(100)

57

40(100)
m = 1,500 2.67
=

ดัง นั้น มะพร้า วคิด เป็น 2.67 % ของต้น ไม้
ยืน ต้น ทั้ง หมด
ตัว อย่า งที่ 14 ร้านจุ๋มจิ๋มขายกล้องตัวหนึ่งไปในราคา
3,800 บาท ปรากฏว่าขาดทุน 5 % ถ้าร้านจุ๋มจิ๋ม
ต้องการกำาไร 10 % ต้องขายสินค้าชนิดนี้ในราคา
เท่าใด
สมมติให้ ราคาทุนของสินค้า c บาท ราคาขาย
3,800 บาท
อัตราส่วนราคาทุนต่อราคาขาย = c : 3,800
ขาดทุน 5 % หมายความว่า ราคาทุน 100 บาท
ขาดทุน 5 บาท ขายไป 95 บาท
อัตราส่วนราคาทุนต่อราคาขาย = 100 : 95
ราคาทุน  ราคาขาย = 100 : 95
c : 3,800 = 100 : 95
c(95) = 100(3,800)

c =
100(3,800)
95
c = 4,000
ราคาทุนของสินค้า = 4,000 บาท
หาราคาขายเพื่อให้ได้กำาไร 10 % หมายความว่า
ราคาทุน 100 บาท กำาไร 10 บาท
ราคาขาย = 100 + 10 = 110 บาท
อัตราส่วนราคาทุนต่อราคาขาย = 100 : 110
สมมติให้ ราคาขายของสินค้า = p บาท
อัตราส่วนราคาทุนต่อราคาขาย = 4,000 :
p

58

ราคาทุน  ราคาขาย = 100 :110
4,000 : p = 100 : 110
4,000(110) = 100(p)
4,000(110)
100 = p
4,400 = p
ดัง นั้น ต้อ งขายสิน ค้า ในราคา 4,400 บาท

วิชา……………………...ห้อง.............เลขที่……….

1. จงเปลี่ยนร้อยละให้อยู่ในรูปเศษส่วน

59

1.1. 4%

=………………………………………………………………
…………………...
1.2. 120%

=………………………………………………………………
…………………...
4
1.3. 6%
5

=………………………………………………………………
…………………...
1.4. 20.25%

=………………………………………………………………
…………………...
1.5. 0.002%

=………………………………………………………………
…………………..

2. จงเปลี่ยนร้อยละให้อยู่ในรูปทศนิยม
2.1. 10%

=…………………………………………………………………
………………..
2.2. 65.3%

=…………………………………………………………………
………………...
2.3. 335%

=…………………………………………………………………
………………...

60

3
2.4. %
7

=…………………………………………………………………
………………...
1
2.5. 2 %
8
8

=…………………………………………………………………
………………..

3. จงเปลี่ยนจำานวนต่อไปนี้ให้อยู่ในรูปร้อยละ
3
3.1.
25

=…………………………………………………………………
………………...
11
3.2.
24

=…………………………………………………………………
………………...
2
3.3. 5
3

=…………………………………………………………………
………………...
3.4. 0.25

=…………………………………………………………………
………………...
3.5. 15.2

=…………………………………………………………………
………………..

61

4. จงหาผลลัพธ์ในแต่ละข้อต่อไปนี้
4.1. 75% ของ 60 มีค่าเท่าไร
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
……………
3
4.2. % ของ 500 มีค่าเท่าไร
5
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
……………
4.3. 30.5% ของ 300 มีค่าเท่าไร
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
……………
4.4. 10 เป็นกี่เปอร์เซ็นต์ของ 25

62

…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
……………………………………………………
4.5. 3 เป็น 15% ของจำานวนใด
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
……………………………………………………

5. จงหาค่าของ 30% ของ 50% ของ 4,500
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
……………………………………………………

6. จงหาค่าของ 100% - (60% x 70%)
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………

63

…………………………………………………………………
……………………………………………………

7. ในโรงเรียนแห่งหนึ่งมีนักเรียน 450 คน ไม่มาเรียน 20% จง
หาจำานวนนักเรียนที่ไม่มาเรียน
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
……………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
………

8. เก็บเงินได้ร้อยละ 5 ของเงินที่หามาได้ ถ้าหาเงินได้ 1,200
บาท จะเก็บเงินได้เท่าไร
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
……………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
………

9. ขายของมีค่านายหน้า 10% ถ้าได้ค่านายหน้า 35 บาท คิด
เป็นราคาของเท่าไร

64

…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
……………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
………

10. มีเป็ดทั้งหมด 250 ตัว เป็ดโตขึ้นปรากฏว่าเหลือเป็ดเพียง
220 ตัว อยากทราบว่าเป็ดตายไป
กี่เปอร์เซ็นต์ของเป็ดทั้งหมด
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
……………………………………………………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
………
…………………………………………………………………
…………………………………………………………………
…………………………………………………………………
………

เฉลยแบบฝึก ทัก ษะที่ 1.1

65

1. จงเขียนอัตราส่วนแสดงการเปรียบเทียบปริมาณ 2 ปริมาณ ดัง
ต่อไปนี้
1.1 นาย ก สูง 170 ซม. นาย ข สูง 165 ซม.
∴ อัตราส่วนความสูงของนาย ก ต่อ นาย ข = 170 :
165
1.2 พี่มีเงิน 50 บาท น้องมีเงิน 20 บาท
∴ อัตราส่วนจำานวนเงินของพี่ต่อน้อง = 50 : 20
1.3 สับปะรด 3 ผล ราคา 33 บาท
∴ อัตราส่วนจำานวนสับปะรดต่อราคา = 3 ผล : 33
บาท
1.4 เงาะ 3 กิโลกรัม ราคา 36 บาท
∴ อัตราส่วนจำานวนเงาะต่อราคา = 3 กิโ ลกรัม :
36 บาท
1.5 ทำางาน 5 วัน ต่อสัปดาห์
∴ อัตราส่วนเวลาทำางานต่อสัปดาห์ = 5
วัน : 1 สัป ดาห์
2. จงทำาให้อัตราส่วนต่อไปนี้ให้เป็นอัตราส่วนอย่างตำ่า
2.1 24 : 36 = 2:3
2.2 35 : 49 = 5:7
2.3 55 : 132 = 5 : 12
2.4 0.96 : 4.8 = 0.02 : 0.1
2.5 51 : 225 = 17 : 75
3. จงหาอัตราส่วนที่เท่ากับอัตราส่วนที่กำาหนดให้มา 3
3.1. 2:3 = 4:6 =6 : 9 = 8 : 12
3.2 7:8 = 14 : 16 =21 : 24
= 28 : 32
3.3 5:6 = 10 : 12 =15 : 18
= 20 : 24
3.4 24 : 36 = 2:3 =4 : 6 = 6 : 9
3.5 60 : 12 = 5:1 = 10 : 2
= 15 : 3
4. จงตรวจสอบว่าอัตราส่วนต่อไปนี้เท่ากัน ( = ) หรือไม่ ( ≠ )
4.1 3:5 ≠ 15 : 10

66

4.2 40 : 32 = 5:4
4.3 4.0 : 6.4 ≠ 1:4
4.4 25 เล่ม : 300 บาท = 5 เล่ม
: 60 บาท
4.5 1 เซนติเมตร : 4,000 เมตร ≠ 4,000
เมตร : 1 เซนติเมตร
5. จงเขียนอัตราส่วนต่อเนื่องต่อไปนี้
5.1 a:b = 4:5
b:c = 5:6
c : d= 1:2
ดังนั้น a : b : c : d = 4 : 5 : 6 : 12
5.2 อายุของต่าย ต่ออายุของต้น เป็น 4 : 5
อายุของต้น ต่ออายุของต้อม เป็น 5 : 7
5.2.1 อัตราส่วนอายุของต่าย ต่ออายุของต้น ต่ออายุของ
ต้อม = 4:5:7
5.2.2 อัตราส่วนอายุของต่าย ต่ออายุของต้อม
= 4:7
5.3 ABCD เป็นรูปสี่เหลี่ยมรูปหนึ่งมีอัตราส่วนของความยาว
ของด้านต่าง ๆ ดังนี้
AB : BC = 4 : 3 , BC : CD = 2 : 3, AD : CD =
1:3
จงเขียนอัตราส่วนของความยาวของด้านต่อไปนี้
5.3.1 AB : BC : CD = 8:6:9
5.3.2 AB : CD = 8:9
5.3.3 BC : CD : AD = 2:3:1
5.3.4 BC : AD = 2:1
5.3.5 AB : BC : CD : AD = 8:6:9:3
6. แปลนบ้านหลังหนึ่งใช้มาตราส่วน 1 : 100 ถ้าความยาว
ของห้องหนึ่งบนแปลนยาว 8.5 เซนติเมตร ความยาวจริงมี
ค่าเท่าใด
วิธ ีท ำา มาตราส่วน 1 : 100 หมายความว่า ถ้าบนแปลน
ยาว 1 ซม. ความยาวจริง
จะเท่ากับ 100 ซม.
ถ้าความยาวบนแปลน 8.5 ซม.
จะมีความยาวจริง = 8.5 × 100 ซม.

67

ดัง นั้น ความยาวจริง มีค ่า = 850 ซม.
ตอบ

7. ในการผสมคอนกรีต จะใช้อัตราส่วนปูน ต่อ กรวด ต่อ ทราย
เป็น 4 : 1 : 3 ถ้าผสมทั้งสามอย่าง
แล้ว ได้ คอนกรี ต หนั ก 720 ตั น จะต้ อ งใช้ ปู น กรวด และ
ทรายอย่างละกี่ตัน
วิธ ีท ำา ส่วนผสมของปูน กรวด ทราย รวมกันได้ = 8
ส่วน
คอนกรีตผสมหนัก 720 ตัน จะต้องใช้ส่วนผสมส่วน
ละ 720 ÷ 8 = 90 ตัน
ดัง นั้น จะต้อ งใช้ป ูน = 90 × 4 =
360 ตัน
กรวด = 90 × 1 = 90 ตัน
ทราย = 90 × 3 = 270 ตั น
ตอบ
8. ในการทำาแชมพูสมุนไพร ประกอบด้วยส่วนผสม อัตราส่วน
ปริมาณหัวแชมพูต่อปริมาณ
ผงข้นต่อปริมาณลาโนลีนต่อปริมาณผงฟองต่อปริมาณนำ้า
มะกรูดต่อปริมาณว่านหางจระเข้
ต่อปริมาณนำ้าสะอาด เท่ากับ 20 : 4 : 2 : 6 : 3 :
10 : 25 ถ้าใช้ลาโนลีน 100 กรัม
จะได้ปริมาณแชมพูสมุนไพรทั้งหมดเท่าไร
วิธ ีท ำา แชมพูสมุนไพรประกอบด้วยส่วนผสม
ปริมาณหัวแชมพูต่อปริมาณผงข้นต่อ
ปริมาณลาโนลีนต่อปริมาณผงฟองต่อปริมาณนำ้ามะกรูด
ต่อปริมาณว่านหางจระเข้ต่อ
ปริมาณนำ้าสะอาด = 20 : 4 : 2 : 6 :
3 : 10 : 25
ถ้าใช้ลาโนลีน 100 กรัม
จะได้ 20 : 4 : 2 : 6 : 3 : 10 : 25
= 20 × 50 : 4 × 50 : 2 × 50 : 6 × 50
: 3 × 50 : 10 × 50 : 25 × 50
= 1,000 : 200 : 100 : 300 :
150 : 500 : 1,250

68

ดัง นั้น ถ้า ใช้ล าโนลีน 100 กรัม จะได้
ปริม าณแชมพูส มุน ไพรทั้ง หมด เท่า กับ
1,000 + 200 + 100 + 300 +
150 + 500 + 1,250 = 3,500 กรัม ตอบ
9. ในการปลูกพืชโครงการเศรษฐกิจพอเพียงของหมู่บ้านแห่ง
หนึ่ง มีพื้นที่ปลูกข้าวต่อพื้นที่ปลูกข้าวโพด เท่ากับ 3 : 2
และมีพื้นที่ปลูกข้าวโพดต่อพื้นที่ปลูกถั่วเหลือง เท่ากับ 7 : 4
ถ้าเขาปลูกข้าว 42 ไร่ พื้นที่ปลูกพืชทั้งหมดเป็นเท่าไร
วิธ ีท ำา อัตราส่วน
พื้นที่ปลูกข้าวต่อพื้นที่ปลูกข้าวโพด = 3 :
2
พื้นที่ปลูกข้าวโพดต่อพื้นที่ปลูกถั่วเหลือง = 7 : 4
ตัวร่วมคือพื้นที่ปลูกข้าวโพด
จะได้ 3 : 2 = 3 × 7 : 2 × 7 = 21 :
14
7 : 4 = 7 × 2 : 4 × 2 =
14 : 8
เขียนอัตราส่วนต่อเนื่องได้
พื้นที่ปลูกข้าวต่อพื้นที่ปลูกข้าวโพดต่อพื้นที่ปลูกถั่ว
เหลือง = 21 : 14 : 8
ถ้าเขาปลูกข้าว 42 ไร่
จะได้ 21 : 14 : 8 = 21 × 2 : 14 × 2 :
8 × 2 = 42 : 28 : 16
ดัง นั้น พื้น ที่ป ลูก พืช ทั้ง หมด = 42 + 28 +
16 = 86 ไร่ ตอบ
10. เหล็กเส้นยาว 30 เมตร แบ่งออกเป็น 3 ส่วนให้ได้
อัตราส่วนความยาวของเหล็กเส้น
ทั้งสามเส้น เท่ากับ 4 : 5 : 6 จงหาความยาวของเหล็ก
เส้นทั้งสามเส้น
วิธ ีท ำา ความยาวเหล็กเส้นทั้งหมด 4 + 5
+ 6 = 15 ส่วน
เหล็กเส้นยาว 30 เมตร
แบ่งเหล็กเส้นยาว 30 เมตร ออกเป็น 15 ส่วน จะ
30
ได้ส่วนละ 15 2 เมตร =

69

ความยาวเหล็กเส้นที่หนึ่งต่อความยาวเหล็กเส้นที่สอง
ต่อความยาวเหล็กเส้นที่สาม
เท่ากับ 4 : 5 : 6 = 4 × 2 : 5 × 2 : 6 × 2
= 8 : 10 : 12
ดัง นั้น ความยาวเหล็ก เส้น ที่ห นึ่ง 8 เมตร
ความยาวเหล็ก เส้น ที่ส อง 10 เมตร
และความยาวเหล็ก เส้น ที่ส าม 12
เมตร ตอบ

1. จงเขียนสัดส่วนทั้ง 2 แบบ พร้อมเติมตัวเลขที่หายไปให้
สมบูรณ์
1 4
ตัวอย่าง 1 : 2 = 4 :8 หรือ 2 = 8
10 30
1.1 10 : 3 = 30 : 9 หรือ 3 = 9
3 6
1.2 3 : 4 = 6 : 8 หรือ 4 = 8
2 6
1.3 2 :3 = 6 :9 หรือ 3 = 9
6
1.4 6 : 17 = 42 : 119 หรือ 17=
42
119
45 15
1.5 45 : 51 = 15 : 17 หรือ 51 = 17

70

2. จงหาค่าของตัวแปรในสัดส่วนต่อไปนี้
24 8
2.1 30= c
c 30
วิธ ีท ำา 8 = 24
30
c = 24
× 8

ดัง นั้น c = 10

a 49
2.2 5 = 35
a 49
49
a = 35
× 5
(b 1
+) 12
2.3 9 = 27
b 1
+ 12
12
b+1 = 27
× 9
b = 4 −1
ดัง นั้น b = 3

5 48
2.4 x 3 = 108
x −3 108
วิธ ีท ำา 5
= 48
108
x −3 = 48
× 5
x = 11 +3
.25
ดัง นั้น x = 14.25

x 8
+ 64
2.5 9 = 72
x +8 64
วิธ ีท ำา 9
= 72
64
x +8 = 72
× 9

71

x = 8 −8

ดัง นั้น x = 0
a
3. กำาหนดให้ a, b, c และ d เป็นสัดส่วนผกผัน และ b =
d
c จงหา
3.1 ค่าของ a เมื่อ b = 7, c = 49, d =
21
a d
วิธ ีท ำา จาก b = c
a 21
จะได้ 7 = 49
21
a = 49
×7


3.2 ค่าของ c เมื่อ a = 3, b = 4, d =
10
a d
3 10
จะได้ 4 = c
4
c = 3
×10

ดัง นั้น c = 13.33

3.3 ค่าของ d เมื่อ a = 0.5, b = 0.8, c =
5.6
a d
0.5 d
จะได้ 0.8 = 5.6
0.5
d = 0.8
×5.6

ดัง นั้น d = 3.5

3.4 ค่าของ b เมื่อ a = 5.2, c = 1.6, d =
1.3
a d

72

5.2 1.3
จะได้ b = 1.6
1.6
b = 1.3
×5.2

ดัง นั้น b= 6.4

3.5 ค่าของ d เมื่อ a = 0.5 , b = 2 , c = 8
a d
0.5 d
จะได้ 2 = 8
0 .5
d = 2
×8

ดัง นั้น d= 2

4. อัตราส่วนของจำานวนผู้ที่ได้ทำางานต่อจำานวนผู้สมัครงานเป็น
2 : 7 ถ้ามีผู้สมัครงาน 910 คน
จะมีผู้ที่ได้ทำางานกี่คน
วิธ ีท ำา ให้ x แทนผู้ที่ได้ทำางาน
7 x
จะได้ 2 = 910
2
x = 7
× 910

x = 260
ตอบ ผู้ท ี่ไ ด้ ท ำา ง า น ทั้ ง ห ม ด มี จ ำา น ว น 260
คน
5. ห้องเรียนห้องหนึ่งมีนักเรียนชาย 4 คน ต่อนักเรียนหญิง 3
คน ถ้านักเรียนห้องนี้ มีทั้งหมด
35 คน จะมีนักเรียนชายและนักเรียนหญิงกี่คน
วิธ ีท ำา ให้ a แทนนักเรียนชาย
4 a
จะได้ 7 = 35
4
=a 7
× 35

=a 20
ต อ บ จ ะ มี น ั ก เ รี ย น ช า ย 20 คน และ
นัก เรีย นหญิง 15 คน
6. ในการทำา งานชิ้นหนึ่งจะใช้จำา นวนคนงานชาย 10 คน จะ
ทำางานชิ้นนั้นเสร็จในเวลา 28 วัน

73

จงหาว่าถ้าใช้คนงานชาย 35 คน จะทำางานชิ้นนั้นเสร็จใน
เวลากี่วัน
วิธ ีท ำา ให้ y แทนจำานวนวันที่ใช้ในการทำางาน
y 10
จะได้ 28 = 35
10
y = 35
× 28

y = 8
ตอบ จ ะ ทำา ง า น เ ส ร็ จ ภ า ย ใ น เ ว ล า 8
วัน
7. เรือ ลำา หนึ่ งมี อ าหารพอกิ นสำา หรั บ 150 คน ได้ นาน 7 วั น
ถ้ามีคนเพียง 70 คน จะกินอาหารได้
นานกี่วัน
วิธ ีท ำา ให้ x แทนจำานวนวันที่จะกินอาหารได้
x 7
จะได้ 150 = 70
7
x = 70
×150

x = 15
ตอบ จะกิน อาหารได้น าน 15 วัน

8. ขั บ รถยนต์ ไ ปจั ง หวั ด หนึ่ ง ด้ ว ยความเร็ ว 60 กิ โ ลเมตรต่ อ
ชั่วโมง ใช้เวลาเดินทาง 3 ชั่วโมงครึ่ง
ถ้า ต้องการใช้เวลาเดินทาง 2 ชั่วโมง จะต้องใช้ความเร็ว
เท่าไร
วิธ ีท ำา ให้ x แทนความเร็ว
x 60
จะได้ 3.5 = 2
60
x = 2
×3.5

x = 105
ตอบ จ ะ ต้ อ ง ใ ช้ ค ว า ม เ ร็ ว 105 กิ โ ล เ ม ต ร ต่ อ

1. จงเปลี่ยนร้อยละให้อยู่ในรูปเศษส่วน
4 1
1.1 4% = 100
= 25

74

120 6
1.2 120% = 100
= 5
4 34 17
1.3 6 % = =
5 500 250
20.25 0.81
1.4 20.25% = 100
= 4
0.002 0.001
1.5 0.002% = 100
= 50
2. จงเปลี่ยนร้อยละให้อยู่ในรูปทศนิยม
2.1. 10% = 0.1
2.2. 65.3% = 0.653
2.3. 335% = 3.35
3
2.4. % = 0.0043
7
1
2.5. 2 % =
8 0.28125
8
3. จงเปลี่ยนจำานวนต่อไปนี้ให้อยู่ในรูปร้อยละ
3
3.1. 25
= 12%
11
3.2. 24
= 45.83%
2
3.3. 5 = 566.66%
3
3.4. 0.25 = 25%
3.5. 15.2 = 1520%
4. จงหาผลลัพธ์ในแต่ละข้อต่อไปนี้
4.1 75% ของ 60 มีค่าเท่าไร
75
วิธ ีท ำา = 100
× 60

= 45

ดัง นั้น 75% ของ 60 มีค ่า = 45
3
4.2 5
% ของ 500 มีค่าเท่าไร
0.6
×500

75

= 3
3
ดัง นั้น 5
% ของ 500 มีค ่า = 3

4.3 30.5 % ของ 300 มีค่าเท่าไร
30.5
× 300

= 91.5

ดัง นั้น 30.5 % ของ 300 มีค ่า = 91.5

4.4 10 เป็นกี่เปอร์เซ็นต์ของ 25
100
×10

= 40

ดัง นั้น 10 เป็น 40% ของ 25

4.5 3 เป็น 15 % ของจำานวนใด
100
×3

= 20

ดัง นั้น 3 เป็น 15% ของ 20

5. จงหาค่าของ 30% ของ 50% ของ 4,500

30 50
วิธ ีท ำา = ×
100 100
× 4,500

= 675

ดั ง นั้ น 30% ของ 50% ของ 4,500 มี ค ่ า =
675

6. จงหาค่าของ 100% - (60% x 70%)
100  60 70 
วิธ ีท ำา = − × 
100  100 100 

= 1 − 0.42

= 0.58

ดัง นั้น มีค ่า = 0.58

76

7. ในโรงเรียนแห่งหนึ่งมีนักเรียน 450 คน ไม่มาเรียน 20% จง
หาจำานวนนักเรียนที่ไม่มาเรียน
20
× 450

= 90

ตอบ นั ก เ รี ย น ที่ ไ ม่ ม า เ รี ย น มี จ ำา น ว น 90
คน
8. เก็บเงินได้ร้อยละ 5 ของเงินที่หามาได้ ถ้าหาเงินได้ 1,200
บาท จะเก็บเงินได้เท่าไร
5
×1,200

= 60

ตอบ จะเก็บ เงิน ได้ 60 บาท

9. ขายของมีค่านายหน้า 10% ถ้าได้ค่านายหน้า 35 บาท คิด
เป็นราคาของเท่าไร
วิธ ีท ำา ให้ x แทนราคาของ
x 100
35
= 10
100
x = ×35 = 350
10

ตอบ ราคาของคิด เป็น 350 บาท
10. มีเป็ดทั้งหมด 250 ตัว เป็ดโตขึ้นปรากฏว่าเหลือเป็ดเพียง
220 ตัว อยากทราบว่าเป็ดตายไป
กี่เปอร์เซ็นต์ของเป็ดทั้งหมด
วิธ ีท ำา เป็ดตายไป 30 ตัว จากเป็ด 250 ตัว และให้ x
แทน % เป็ดที่ตายไป
30 x
จะได้ 250
= 100
30
x = ×100
250
= 12
ตอบ เป็ด ตายไป 12 % ของเป็ด ทั้ง หมด

77

แบบทดสอบก่อ นเรีย น – หลัง เรีย น
หน่ว ยที่ 1 อัต ราส่ว น สัด ส่ว น ร้อ ยละ
คำา ชี้แ จง ให้นักเรียนทำาเครื่องหมาย (×) ลงในช่อง  ของ
กระดาษคำาตอบที่กำาหนดให้
โดยเลือกข้อที่ถูกต้องที่สุดเพียงข้อเดียว

1. อัตราส่วนการลงทุนของหนู หากสิ้นปีบริษัทมีกำาไร
นา  น้องไก่ เท่ากับ 3 : 7

78

200,000 บาท น้องไก่จะ 5. ขนมปังมีส่วนผสมดังนี้ แป้ง
ได้รับส่วนแบ่งกำาไรกี่บาท  นำ้าตาล  เนย เท่ากับ 5 :
ก. 100,000 บาท 4 : 1 ถ้ามีแป้ง 100 กรัม
ข. 200,000 บาท จะต้องใช้เนยกี่กรัม
ค. 140,000 บาท 1. 20 กรัม
ง. 160,000 บาท 2. 30 กรัม
2. ในการผสมนำ้าเชื่อม 5 ถ้วย 3. 40 กรัม
จะต้องใช้นำ้าตาล 2 ถ้วย 4. 50 กรัม
นำ้า 3 ถ้วย ถ้าต้องการนำ้า 6. m : 5 = 14 : 35
เชื่อม 15 ถ้วย จะต้องใช้ ค่า m เท่ากับข้อใด
นำ้ากี่ถ้วย 1. 1
1. 3 ถ้วย 2. 2
2. 5 ถ้วย 3. 5
3. 6 ถ้วย 4. 7
4. 9 ถ้วย
7. 5 : 9 = (m + 2) : 81
3. ในการทำาผัดเผ็ดไก่ จะต้อง ค่า m เท่ากับข้อใด
ใช้เครื่องแกง 200 กรัมต่อ 1. 39
เนื้อไก่ครึ่งกิโลกรัม ถ้าซื้อ 2. 41
เนื้อไก่มา 5 กิโลกรัม จะ 3. 43
ต้องใช้เครื่องแกงกี่กรัม 4. 45
1. 1,000 กรัม
2. 2,000 กรัม 8. 10 : m = 5 : 13
3. 2,400 กรัม ค่า m – 5 เท่ากับข้อใด
4. 2,600 กรัม 1. 16
2. 21
4. โลหะผสมชนิดหนึ่ง ต้องใช้ 3. 26
ส่วนผสมเหล็ก  ทองแดง  4. 31
นิเกิล เท่ากับ 7 : 4 : 3 ถ้าต
9. รูปสี่เหลี่ยมผืนผ้ารูปหนึ่งมี
ต้องการโลหะผสม 140
อัตราส่วนของความกว้างต่อ
กิโลกรัม จะต้องใช้ส่วนผสม
ความยาวเป็น 5 : 8 ถ้ารูป
เหล็ก  ทองแดง  นิเกิล
เท่ากับข้อใด สี่เหลี่ยม
1. 14 : 8 : 6
ผืนผ้านี้มีความยาวของเส้น
รอบรูป 78 เซนติเมตร
2. 28 : 16 : 12
ความกว้างและความยาวของ
3. 35 : 20 : 15
รูป
4. 70 : 40 : 30

79

สี่เหลี่ยมผืนผ้านี้มีค่าเท่ากับ ก. 240
ข้อใด ข. 300
ก. 15 เซนติเมตร และ ค. 400
24 เซนติเมตร ง. 480
ข. 10 เซนติเมตร และ 13. ข้อใดมีค่าไม่เ ท่า กับ 75
29 เซนติเมตร %
ค. 20 เซนติเมตร และ ก. 3 : 4
25 เซนติเมตร ข. 15 : 20
ง. 12 เซนติเมตร และ
ค. 0.75
21 เซนติเมตร
ง. 10 : 75
10. ทหาร 60 คน กินข้าว
14. 15 % ของ 20 % ของ
จำานวนหนึ่งหมดภายใน 20
100,000
วัน อยากทราบว่า ทหาร
มีค่าเท่ากับข้อใด
40 คน กินข้าวจำานวนเท่า
ก. 3,000
เดิมหมดภายในเวลากี่วัน
ข. 10,000
ก. 15 วัน
ค. 15,000
ข. 20 วัน
ง. 20,000
ค. 25 วัน
ง. 30 วัน 15. นักเรียน ปวช. 1/2
บัญชี มาเรียนวิชา
11. นายสุวิชชา มีรายได้
คณิตศาสตร์ประยุกต์ 1
เดือนละ 8,000 บาท
จำานวน 42 คน ขาดเรียน
จ่ายค่าอาหาร 30 % นายสุ
จำานวน 3 คน นักเรียนที่
วิชชาจ่ายค่าอาหารเดือนละ
ขาดเรียนคิดเป็นร้อยละ
เท่าใด
เท่าใด
ก. 2,400 บาท
ของนักเรียนทั้งหมด
ข. 2,600 บาท
ก. 15 %
ค. 2,700 บาท
ข. 20 %
ง. 2,800 บาท
ค. 25 %
12. 120 คิดเป็น 40 % ของ ง. 30 % 66
จำานวนใด
เฉลยแบบทดสอบก่อ นเรีย น – หลัง เรีย น
หน่ว ยที่ 1 อัต ราส่ว น สัด ส่ว น ร้อ ยละ

80

1. ค 6. ข 11. ก
2. ง 7. ค 12. ข
3. ข 8. ก 13. ง
4. ง 9. ข 14. ค
5. ก 10. ง 15. ค

.

หน่วยที่1อัตราส่วนสัดส่วนและร้อยละ

More Related Content

What's hot

Similar to หน่วยที่1อัตราส่วนสัดส่วนและร้อยละ

หน่วยที่1อัตราส่วนสัดส่วนและร้อยละ