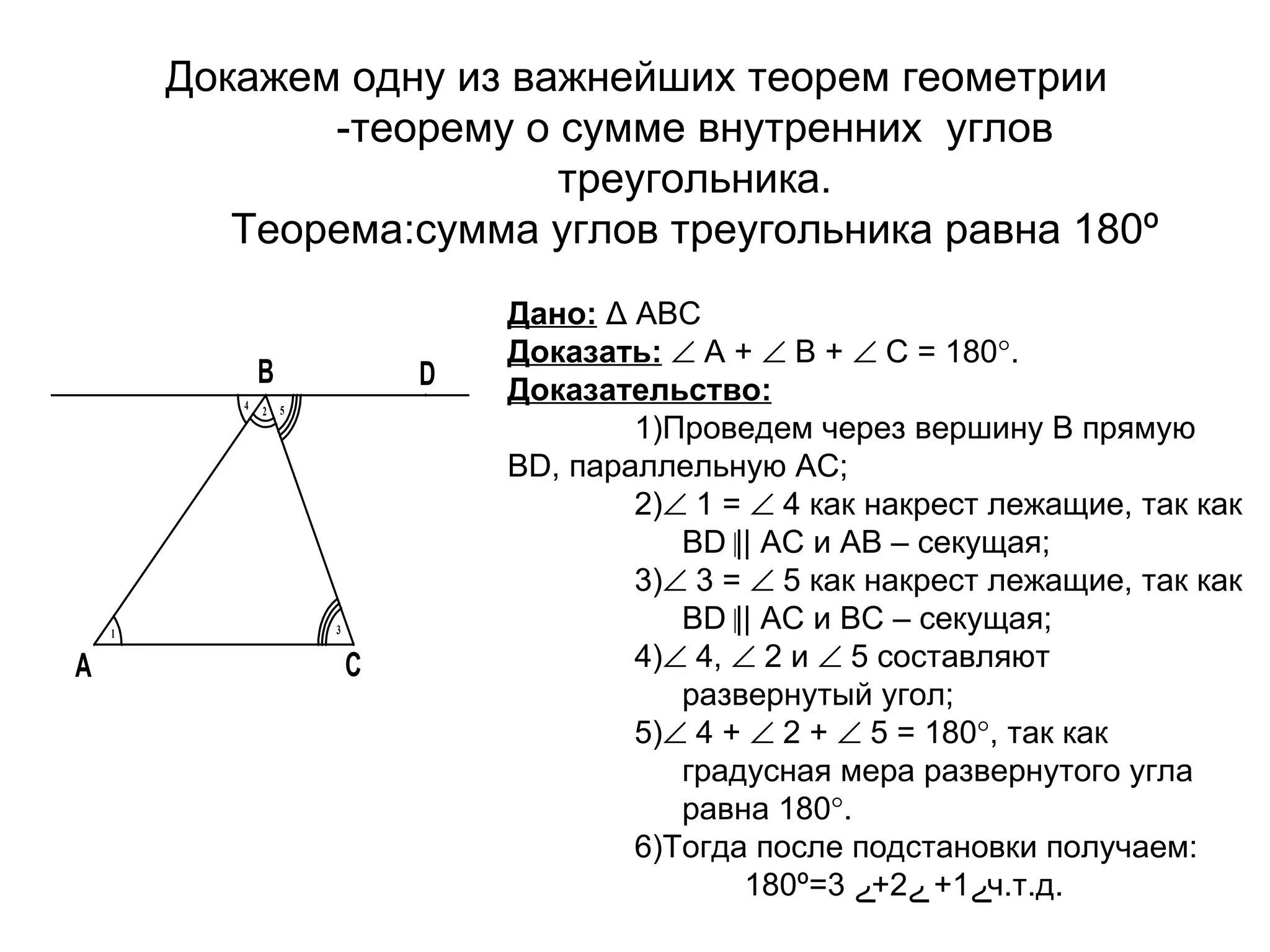
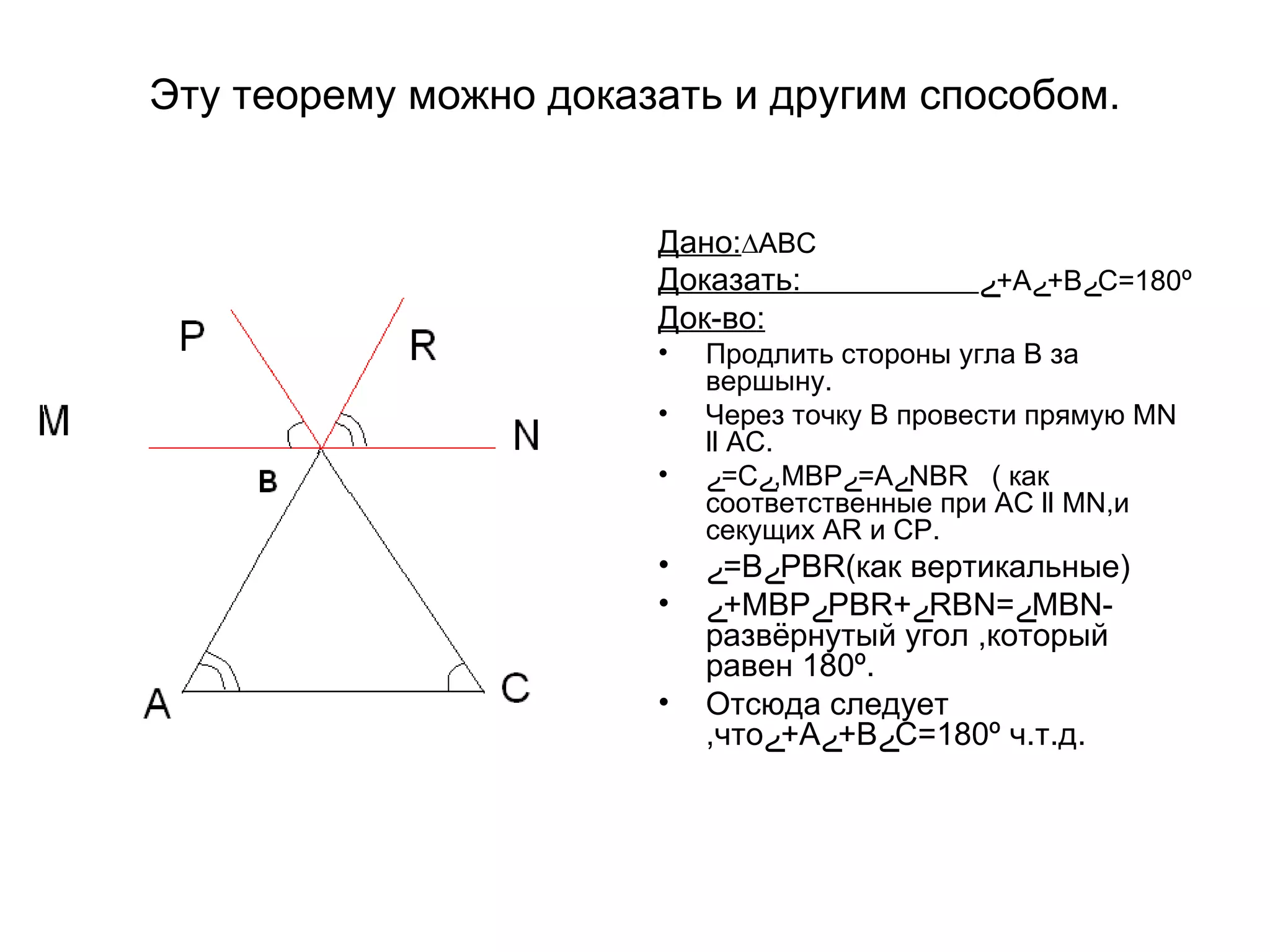
Презентация Михаила Ступакова из 10 'А' класса посвящена теореме о сумме внутренних углов треугольника, утверждающей, что сумма углов треугольника равна 180°. Доказывается эта теорема с использованием геометрических понятий и методов, таких как накрест лежащие углы и параллельные прямые. Также приводятся следствия из теоремы, в частности, о том, что в любом треугольнике два угла острые.

1. Тема : Сумма внутренних углов треугольника Презентация ученика 10 “ а ” класса Ступакова Михаила.

2. Докажем одну из важнейших теорем геометрии -теорему о сумме внутренних углов треугольника. Теорема : сумма углов треугольника равна 180 º Дано: Δ АВС Доказать:  А +  В +  С = 180  . Доказательство: 1)Проведем через вершину В прямую В D , параллельную АС; 2)  1 =  4 как накрест лежащие, так как В D ‌‌‌‌‌‌|| АС и АВ – секущая; 3)  3 =  5 как накрест лежащие, так как В D ‌‌‌‌‌‌|| АС и ВС – секущая; 4)  4,  2 и  5 составляют развернутый угол; 5)  4 +  2 +  5 = 180  , так как градусная мера развернутого угла равна 180  . 6)Тогда после подстановки получаем : ے 1+ ے 2+ ے 3=180º ч.т.д.

3. Эту теорему можно доказать и другим способом. Дано : ∆АВС Доказать : ے А+ ے В+ ے С=180 º Док-во : Продлить стороны угла В за вершыну. Через точку В провести прямую М N ll АС. ے С= ے МВР, ے А= ے NBR ( как соответственные при АС ll М N ,и секущих AR и СР. ے В= ے РВ R (как вертикальные) ے МВР+ ے РВ R+ ے RBN = ے МВ N- развёрнутый угол ,который равен 180 º . Отсюда следует ,что ے А+ ے В+ ے С=180 º ч.т.д.

4. Следствие Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. Доказательство : Пусть дан Δ ABC . Точка D лежит на прямой AC так, что точка A лежит между C и D . Тогда ے BAD – внешний к углу треугольника при вершине A и ے A + ے BAD = 180°. Но ے A + ے B + ے C = 180°, и, следовательно, ے B + ے C = 180° – ے A . Отсюда ے BAD = ے B + ے C . Следствие доказано. Рисунок 4.4.2.

5. Докажем ещё одно следствие : у любого треугольника два угла острые. Из теоремы следует, что у любого треугольника два угла острые. Действительно, применяя доказательство от противного , допустим, что у треугольника только один острый угол или вообще нет острых углов. Тогда у этого треугольника есть, по крайней мере, два угла, каждый из которых не меньше 90°. Сумма этих углов не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°. Что и требовалось доказать.