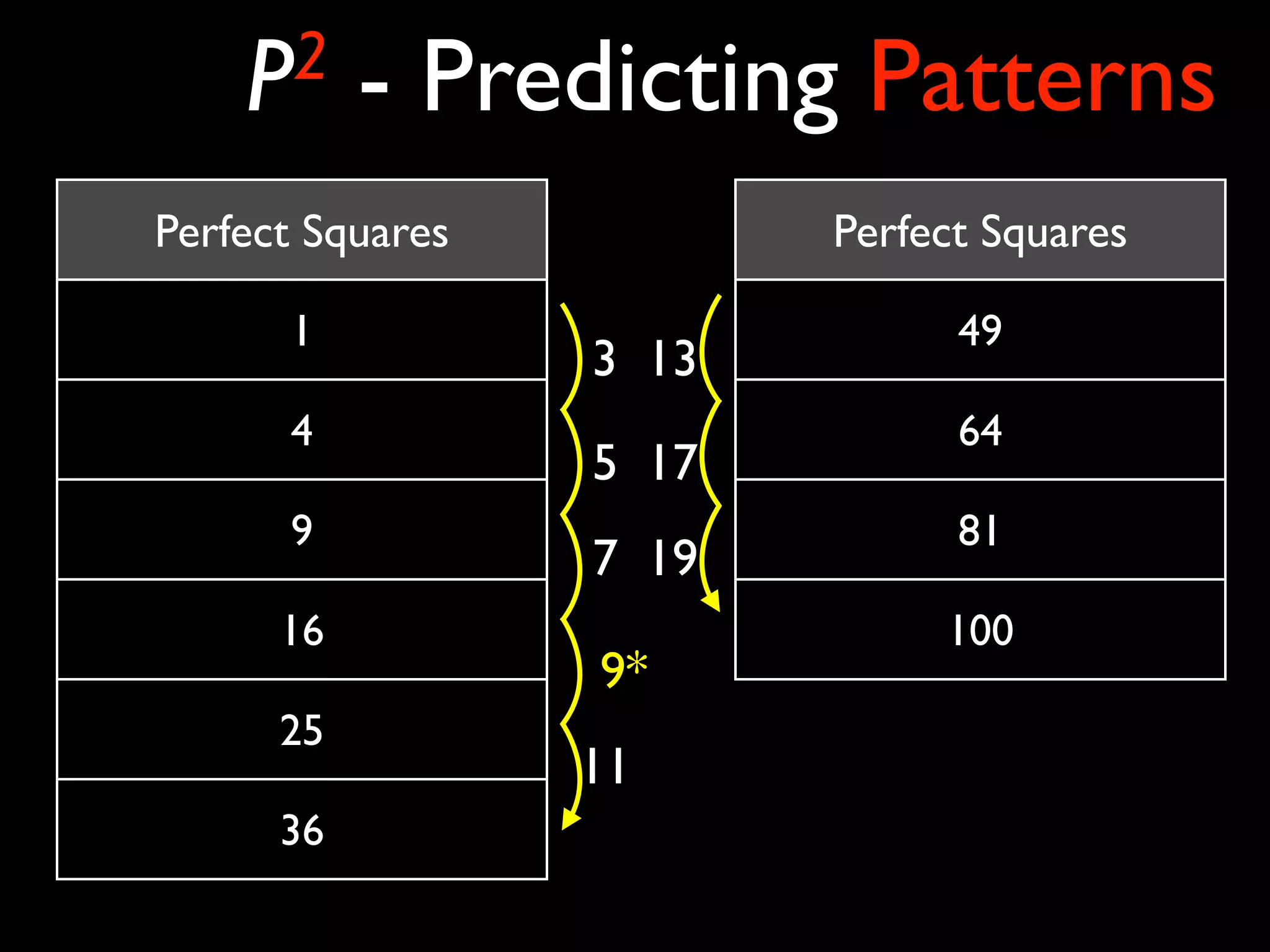
The document focuses on predicting mathematical patterns related to perfect squares and prime numbers, emphasizing their characteristics and relationships. It presents prime factorization as a method for finding square roots of larger square numbers and provides examples for practice. Additionally, it discusses the patterns in the ones position of square numbers.

1. Extending Your Knowledge
Grade 8 Mathematics
Mr. J. Lingley

2. P2 - Predicting Patterns
Perfect Squares
1
4
9
16
25
36
3
5
7
9*
11
Perfect Squares
49
64
81
100
13
17
19

3. P2 - Predicting Patterns
3 5 7 11 13 17 19
2
What do all of these have in common?

4. P2 - Predicting Patterns
3 5 7 11 13 17 19
What do all of these have in common?
They are prime numbers.
2

5. List of Square Numbers
Looking at the ones position, do you see any patterns?
1 4 9 16 25 36 49 64 81 100 121 144 169 196 225
256 289 324 361 400 441 484 529 576 625 676 729 784 841 900
961 1024 1089 1156 1225 1296 1369 1444 1521 1600 1681 1764 1849 1936 2025
2116 2209 2304 2401 2500 2601 2704 2809 2916 3025 3136 3249 3364 3481 3600

6. List of Square Numbers
Looking at the ones position, do you see any patterns?
1 4 9 16 25 36 49 64 81 100 121 144 169 196 225
256 289 324 361 400 441 484 529 576 625 676 729 784 841 900
961 1024 1089 1156 1225 1296 1369 1444 1521 1600 1681 1764 1849 1936 2025
2116 2209 2304 2401 2500 2601 2704 2809 2916 3025 3136 3249 3364 3481 3600
All square numbers end in 1, 4, 9, 6, 5, or 00

7. Prime Factorization
A long word, for a very long (but geeky) process.
Say we want to find the square root of a larger square number like 441.
Might seem impossible, but all we need to
remember are a couple of math strategies.

8. Prime Factorization
A long word, for a very long (but geeky) process.
Say we want to find the square root of a larger square number like 784.
√784 What do we notice about this number?
Let’s think about our divisibility rules...

9. Prime Factorization
A long word, for a very long (but geeky) process.
Say we want to find the square root of a larger square number like 784.
√784 What do we notice about this number?
Let’s think about our divisibility rules...
Since this is an even number,
it must be divisible by 2.

10. Prime Factorization
A long word, for a very long (but geeky) process.
Say we want to find the square root of a larger square number like 784.
√784 What do we notice about this number?
Let’s think about our divisibility rules...
Since this is an even number,
it must be divisible by 2.
We now use the smallest prime number (2) to simplify 784.

11. √784
√ 2 x 392
√ 2 x 2 x 196
√ 2 x 2 x 2 x 98
√ 2 x 2 x 2 x 2 x 49
√ 2 x 2 x 2 x 2 x 7 x 7
( 2 x 2 x 7 ) x ( 2 x 2 x 7 )
√ ( 28 ) x ( 28 ) = 28

12. Your Turn
1. Using prime factorization, find the square roots of:
√225 √484 √324
2. Which of the following numbers is a square number?
How do you know?
√_ _ 8 √_ _ 6
√_ _ _ _ 9 √_ _ _ _ _ 2