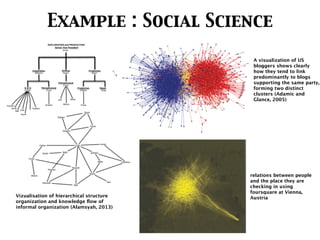
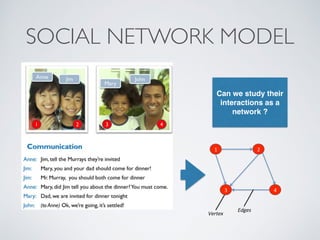
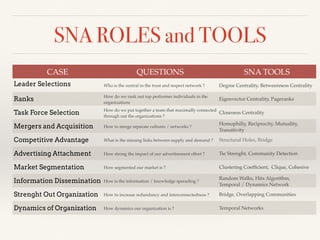
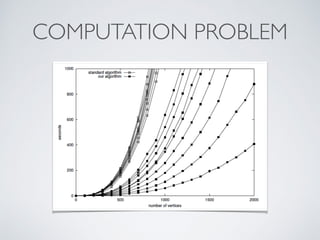
The document discusses the complexities of social networks, emphasizing the need for advanced metrics and computational methods to analyze social interactions. It highlights key concepts such as homophily, transitivity, and bridge connections within networks, as well as various centrality measures used for analyzing social ties. The document also includes examples of community detection and applications within organizational contexts to illustrate the importance of network structure in social computing.

1. SOCIAL NETWORK, METRICS
AND COMPUTATIONAL
PROBLEM
Andry Alamsyah
andrya@telkomuniversity

2. GLOBAL SCALE OF SOCIAL
NETWORK

3. GLOBAL SCALE OF SOCIAL
NETWORK

4. GLOBAL SCALE SOCIAL
NETWORK

5. Example : Social Science
A visualization of US
bloggers shows clearly
how they tend to link
predominantly to blogs
supporting the same party,
forming two distinct
clusters (Adamic and
Glance, 2005)
Vizualisation of hierarchical structure
organization and knowledge flow of
informal organization (Alamsyah, 2013)
relations between people
and the place they are
checking in using
foursquare at Vienna,
Austria

6. STORY
• BIG DATA leads to Social
Computing
• Social Network Data / Conversation
are widely available
• The Need of Powerful Metric for
Social Network
• Problem with Conventional
Methodology Approach using
Questionnaire and Interviews

7. SOCIAL NETWORK MODEL
Can we study their
interactions as a
network ?
3" 4"
2"1"
Vertex&
Edges&

8. SOCIAL NETWORK MODEL
3" 4"
2"1"
Vertex" Vertex"
1" 2"
1" 3"
2" 3"
2" 4"
4" 3"
Edges&List&
Adjacency&Matrix&become"symmetric&
Vertex" 1" 2" 3" 4"
1" 2" 1" 1" 0"
2" 1" 2" 1" 1"
3" 1" 1" 2" 0"
4" 0" 1" 0" 2"3" 4"
2"1"
Directed&
(who&contact&whom)&
Undirected&
(who&knows&whom)&

9. 3" 4"
2"1"
30"
5" 2"22"
37"
Weight"could"be"
5 Frequency"of"interac=ons"in"
period"of"observa=on"
5 Number"of"items"exchanged"in"
period"
5 Individual"percep=ons"of"
strength"of"rela=onship"
5 Cost"of"communica=ons"or"
exchange,"e.g."distance"
Vertex" Vertex" Weight"
1" 2" 30"
1" 3" 5"
2" 3" 22"
2" 4" 2"
4" 3" 27"
Edges&List&
Adjacency&Matrix&(weight)&
Vertex" 1" 2" 3" 4"
1" 5" 30" 5" 0"
2" 30" 5" 22" 2"
3" 5" 22" 5" 37"
4" 0" 2" 37" 5"
TIE-STRENGTH

10. Edge Weights as Relationship Strength
• Edges can represent interactions, flows of
information or goods, similarities/affiliations, or social
relations
• Specifically for social relations, a ‘proxy’ for the
strength of a tie can be:
• the frequency of interaction (communication) or
the amount of flow (exchange)
• reciprocity in interaction or flow
• the type of interaction or flow between the two
parties (e.g., intimate or not)
• other attributesof the nodes or ties (e.g., kin
relationships)
• The structure of the nodes’ neighborhood (e.g.
many mutual ‘friends’)
• Surveys and interviews allows us to establish the
existence of mutual or one-sided strength/affection
with greater certainty, but proxies above are also
useful

11. • Homophily is the tendency to relate to people with similar
characteristics (status, beliefs, etc.)
• It leads to the formation of homogeneous groups
(clusters) where forming relations is easier
• Extreme homogenization can act counter to innovation
and idea generation (heterophily is thus desirable in
some contexts)
• Homophilous ties can be strong or weak
• Transitivity in SNA is a property of ties: if there is a tie
between A and B and one between B and C, then in a
transitive network A and C will also be connected
• Strong ties are more often transitive than weak ties;
transitivity is therefore evidence for the existence of
strong ties (but not a necessary or sufficient condition)
• Transitivity and homophily together lead to the formation
of cliques (fully connected clusters)
• Bridges are nodes and edges that connect across groups
• Facilitate inter-group communication, increase social
cohesion, and help spur innovation
• They are usually weak ties, but not every weak tie is a
bridge
Homophily, Transitivity, and Bridge

12. NETWORK MODEL EXAMPLE

13. CENTRALITY
paper: Mapping Network of Terrorist Cells - V.E.Krebs (2002)

14. COMMUNITY DETECTION
collaboration network of
scientist at Santa Fe Institut
(Girvan & Newman)
271 scientist (vertices) / 118
nodes from largest component
edge = scientist coauthor one
of more publications
Komunitas : kumpulan titik titik
dimana jumlah hubungan internal
antar titik lebih besar dari pada
jumlah hubungan dengan titik
eksternal
paper: Community Structure in Social and Biological Networks - Girvan-Newman (2002)

15. SNA ROLES and TOOLS
CASE QUESTIONS SNA TOOLS
Leader Selections Who is the central in the trust and respect network ? Degree Centrality, Betweenness Centrality
Ranks How do we rank out top performer individuals in the
organizations
Eigenvector Centrality, Pageranks
Task Force Selection How do we put together a team that maximally connected
through out the organizations ?
Closeness Centrality
Mergers and Acquisition How to merge separate cultures / networks ?
Homophilly, Reciprocity, Mutuality,
Transitivity
Competitive Advantage What is the missing links between supply and demand ? Structural Holes, Bridge
Advertising Attachment How strong the impact of our advertisement effort ? Tie Strenght, Community Detection
Market Segmentation How segmented our market is ? Clustering Coefficient, Clique, Cohesive
Information Dissemination How is the information / knowledge spreading ?
Random Walks, Hits Algorithm,
Temporal / Dynamics Network
Strenght Out Organization How to increase redundancy and interconnectedness ? Bridge, Overlapping Communities
Dynamics of Organization How dynamics our organization is ? Temporal Networks

16. PREFERENTIAL ATTACHMENT
model barabasi-albert

17. SOCIAL NETWORK SIMULATION
community detection
centrality
*karate club dataset
34 nodes dan 78 edges
model network
community detection result
degree centrality result

18. METRIK CENTRALITY
betweenness centrality
banyaknya jalur terpendek antar
pasangan semua titik di jaringan, yang
melewati satu titik yang diukur
closeness centrality
jarak titik yang diukur terhadap
semua titik yang ada dalam jaringan

19. KOMPLEKSITAS CENTRALITY
CB (i) =
σst (i)
σsts≠i≠t
∑
Betweenness Centrality Closenness Centrality
s=1 s=2 s=3
t=5 1/1 2/2 1/1
t=6 1/1 2/2 1/1
t=7 2/2 4/4 2/2
t=8 2/2 4/4 2/2
t=9 2/2 4/4 2/2
σst (4) /σst
CB (4) = 15
Cc (i) =
n −1
dij
j(≠i)
∑
1 2 3 4 5 6 7 8 9
1 0 1 1 1 2 2 3 3 4
2 1 0 1 2 3 3 4 4 5
3 1
1 0 1 2 2 3 3 4
4 1 2 1 0 1 1 2 2 3
5 2 3 2 1 0 1 1 1 2
6 2 3 2 1 1 0 1 1 2
7 3 4 3 2 1 1 0 1 1
8 3 4 3 2 1 1 1 0 2
9 4 5 4 3 2 2 1 2 0
Cc (4) = 0,62 Cc (3) = 0,47
*kompleksitas waktu perhitungan metrik mencapai
O(n3) dan kompleksitas ruang sebesar O(n2)

20. METRIK MODULARITY
edges inside the
community
expected number of edges
if i,j places at random
Metrik Modularity
indeks kualitas partisi jaringan
menjadi komunitas
Kompleksitas Metrik
kompleksitas waktu perhitungan
O(n3)

21. COMPUTATION PROBLEM

22. COMPUTATION STRATEGY
• Select Features
• Random / Strategic Sampling
• Transform Model
• Compress Graph

23. TERIMA KASIH
THANK YOU