This document discusses studies on measures of intuitionistic fuzzy information. It begins with introductions and definitions related to fuzzy sets, intuitionistic fuzzy sets, and measures of fuzzy entropy. It then discusses special t-norm operators and proposes a measure of intuitionistic fuzzy entropy based on these t-norms. The measure is defined using a function of the membership, non-membership, and hesitancy degrees of an intuitionistic fuzzy set. Several desirable properties of such a measure are outlined, including sharpness, maximality, resolution, symmetry, and valuation. The document provides mathematical foundations and definitions to propose and analyze a measure of intuitionistic fuzzy entropy.

1. STUDIES ON INTUTIONISTIC FUZZY
INFORMATION MEASURE
Ist International Conference of ISITA
on
Mathematical Modeling, Optimization and Information Technology
SSCET, Badhani, Pathankot, Punjab
1
INFORMATION MEASURE
Surender Singh
Assistant Prof.
School of Mathematics, Faculty of Sciences
Shri Mata Vaishno Devi University
Katra –182320 (J & K)
Email:surender1976@gmail.com
16th -19th Jan., 2015

2. OUTLINE
 INTRODUCTION AND PRELIMINARIES
 SPECIAL T-NORM
 INTUTIONISTIC FUZZY ENTROPY
EXAMPLES OF REF’s AND NEW MEASURE
2
 EXAMPLES OF REF’s AND NEW MEASURE
OF IFE
 CONCLUDING REMARKS

3. 1. INTRODUCTION AND PRELIMINARIES
 Fuzziness, a feature of imperfect information, results from the lack of
crisp distinction between the elements belonging and not belonging to a
set (i.e. the boundaries of the set under consideration are not sharply
defined).
 The concept of fuzziness initiated by [Zadeh, 1965].
 [De Luca and Termini, 1971] introduced some requirements which
capture our intuitive comprehension of the degree of fuzziness in a fuzzycapture our intuitive comprehension of the degree of fuzziness in a fuzzy
set and introduced concept of fuzzy entropy.
 The term ‘Fuzzy entropy’ have been adopted due to an intrinsic
similarity of equation to the one in the [Shannon, 1948] entropy.
 Two functions measure fundamentally different types of uncertainty.
Basically, the Shannon entropy measures the average uncertainty in bits
associated with the prediction of outcomes in a random experiment.
3

4.  The idea of intutionistic fuzziness initiated by [Atanassov, 1986] and
incidentally affected all fields of study where ever concept of
fuzziness was used. [Vlachos et al., 2007] derived an extension of
De Luca- Termini’s entropy for IFSs. In this paper, we study
measure of fuzziness for intuitionistic fuzzy sets in light of restricted
equivalence functions and T-norm operator.
4

5. Definition 1.1.1[Bustince et al., 2006] Let cc ],1,0[]1,0[:  is a fuzzy
negation iff:
N1: 1)0( c and ,0)1( c
N2: yxifycxc  ,)()( (monotonicity).
A fuzzy negation is strict, iff,
N3: )(xc is continuous.
N4: yxifycxc  ,)()( for all ].1,0[, yx
5
N4: yxifycxc  ,)()( for all ].1,0[, yx
A strict fuzzy negation is involutive, iff,
N5: ),())(( xcxcc  ].1,0[x
The strict fuzzy negations that are involutive are called strong negations.

6. Definition 1.1.2[Bustince et al., 2006] A function ]1,0[]1,0[: 2
REF is called a
restricted equivalence function, if it satisfies the following conditions:
R1: ),(),( xyREFyxREF  for all ];1,0[, yx
R2: 1),( yxREF iff ;yx 
R3: 0),( yxREF iff 1x and 0y or 0x and ;1y
R4: ))(),((),( ycxcREFyxREF  for all ],1,0[, yx c being a strong negation;
R5: For all ],1,0[,, zyx if ,zyx  then ),(),( zxREFyxREF 
and
6
and .),(),( zxREFzyREF 
It can be proved that R5 is equivalent to: for all x, y, z, t [0, 1], if
,tzyx  then .),(),( txREFzyREF 

7. 1.2 Intutionistic fuzzy sets
Let X be an ordinary non-empty, finite set. Then an IFS over X is
characterized by two mappings ]1,0[: Xg and ].1,0[: Xh
For each )(, xgXx can be interpreted as the degree to which x enjoys some
property P. Alternately, )(xh is the degree to which x does not enjoy the
property P. Here, g and h are the generalizations of characteristic function
of conventional set theory. There is nothing intutionally fuzzy about set X.
Rather, the fuzziness lies in the degree of compatibility and the degree of
7
Rather, the fuzziness lies in the degree of compatibility and the degree of
incompatibility of the element Xx with property P.
Definition 1.2.1. An intutionistic fuzzy set A defined on a universe X is
given by [Atanassov, 1986]:
},|))(),(,{( XxxhxgxA AA 

8. where,
]1,0[: XgA and ]1,0[: XhA , with the condition ,1)()(0  xhxg AA for all Xx .
The numbers )(xgA and )(xhA denotes the degree of membership and the
degree of non membership of x to A, respectively. For all IFS A in X we
call the intutionistic index of an element Xx in A the following
expression:
).()(1)( xhxgx AAA 
we consider )(xA as a hesitancy degree of x to A.
Evidently, for all .
8
Evidently, 1)(0  xA for all Xx  .
1.2 Fuzzy Entropy
In fuzzy set theory, the entropy is measure of fuzziness which expresses
the amount of average ambiguity /difficulty in taking a decision weather
an element belong to a set or not. A measure of fuzziness H (A) of a fuzzy
set A should have the at least the following four properties .

9. FE1 (Sharpness): H (A) is minimum if and only if A is crisp set, that is,
A(X) =0 or 1 for all .Xx 
FE2 (Maximality): H (A) is maximum if and only if A is most fuzzy
set, that is, A(X) =0.5 for all .Xx 
FE3 (Resolution): H (A)H(A*),where A* is the sharpened version of
A.
FE4(Symmetry):H(A)=H(),where is the complement set of A , that
is ,(x)=1- A(x) for all .Xx 
9
[Ebanks, 1993] proposed one more axiom as essential condition for
validity of a measure of fuzzy entropy
FE5 (Valuation): )()()()( BHAHBAHBAH  .
[DeLuca and termini, 1971] introduced a measure of fuzziness
analogous to the information theoretic entropy of [Shannon, 1948] as
 

n
i
iAiAiAiA xxxx
n
AH
1
))(1log())(1()(log)(
1
)(  .

10. 2. Special T-Norm
The truth table of the classical binary conjunction ^ is given in Table
1. In many-valued logic we extend the classical binary conjunction to
the unit interval as a ]1,0[]1,0[ 2
 mapping as follows:
Definition 2.1 [Schweizer and Sklar, 1960] A mapping ]1,0[]1,0[: 2
C is a
conjunction on the unit interval if it satisfies:
C1.Boundary conditions: C(0, 0) = C(0, 1) = C(1, 0) = 0 and C(1, 1) = 1,C1.Boundary conditions: C(0, 0) = C(0, 1) = C(1, 0) = 0 and C(1, 1) = 1,
Table 1: Truth table of the classical binary conjunction
p q qp 
0 0 0
0 1 0
1 0 0
1 1 1
10

11. C2. Monotonicity: )]1,0[),,(( 3
 zyx )),(),(),(),(( yzCxzCandzyCzxCyx 
Definition 2.2 [Schweizer and Sklar, 1960] A mapping ]1,0[]1,0[: 2
T is a
triangular norm
(t-norm for short) if for all 2
]1,0[,, zyx it satisfies:
T1. Boundary condition: ,)1,( xxT T1. Boundary condition:
T2. Monotonicity: ),(),( zxTyxTzy  ,
T3. Symmetry: ),(),( xyTyxT  ,
T4. Associativity: )),,(()),(,( zyxTTzyTxT  .
A t-norm T always satisfies .]1,0[),(  xxxxT
If we put a restriction on T that ]1,0[1),(  xxxT .
11

12. Now this idea of this t-norm may further be extended as follows:
Definition 2.3 A mapping ]1,0[]1,0[]1,0[:  nnR
T is a special triangular
norm if for all
]1,0[,,]1,0[)...,,,(),...,,,(),...,,,( 212121  iii
n
nnn zyxandzzzyyyxxx zyx it satisfies:
RT1. Boundary condition: ,)( x1x, R
T
RT2. Monotonicity: ),(),( zxyxzy RR
TT  ,
RT3. Symmetry: ),(),( xyyx RR
TT  ,RT3. Symmetry: ),(),( xyyx RR
TT  ,
RT4. R
T is permutationally symmetric,
RT5. Associativity: )),,(()),(,( zyxzyx RRRR
TTTT  ,
RT6. nR
T ]1,0[),(  x1xx ,
RT7. .]1,0[),(),(),( nRRR
TTT  xy00xyx
12

13. 3. Intutionistic Fuzzy Entropy
Let ]}1,0[:|{]1,0[  XggX
g and ]}1,0[:|{]1,0[  XhhX
h then a measure of
degree of intutionistic fuzziness is a non negative function
]1,0[]1,0[]1,0[:  X
h
X
gd such that a functional can be regarded as an entropy in
the sense that it measures our uncertainty about the presence, absence or
indeterminacy of some property P over X.
Some desirable properties of intutionistic fuzzy entropy:
Intutionistic fuzziness of a set XA  is characterized by two functions
]1,0[: XgA and ]1,0[: XhA , with the condition ,1)()(0  xhxg AA for all
Xx  .
we have X
gAg ]1,0[ and X
hAh ]1,0[ .
Let }...,,,{ 21 nxxxX  , )...,,,( 21 ngggAg with nixgg iAi ...,,2,1),(  and
)...,,,( 21 nhhhAh with nixhh iAi ...,,2,1),(  .
13

14. Here, following facts are clear:
(i) XX
h
X
g ]1,0[]1,0[]1,0[  .
(ii) n
timesn
]1,0[]1,0[...]1,0[]1,0[ 
  Ag and n
timesn
]1,0[]1,0[...]1,0[]1,0[ 
  Ah .
Let ),( AA hgf , we say .]1,0[]1,0[ nn
f 
Now, define
),()...,,,,...,,,(),()( 2121 AAAA hghg R
termsn
n
termsn
n
R
ThhhgggTdfd 

, (1)
for some function ]1,0[]1,0[]1,0[:  XXR
T (definition 2.3)
,Now it is convenient to impose a lattice structure on XX
]1,0[]1,0[  , as
follows:
Let XX
ff ]1,0[]1,0[,  be such that ),( AA hgf and ),( AA hg f .
we define
)})(),(.{min},)(),(.{(max),( xhxhxgxghhggff AAAAAAAA
 and
)})(),(.{max},)(),(.{(min),( xhxhxgxghhggff AAAAAAAA
 .
14

15. From the above notions, a list of essential properties for measure of
intutionistic fuzziness follows.
P1 Sharpness: We have, 0)( fd i.e. 0),( AA hgR
T iff. },1,0{)(),( XhXg AA i.e.
Ag and Ah are sharp.
P2 Maximality: ),(),()( AA hgR
AA Thgdfd  attains its maximum value only
when AA hg  i.e. .AA hg 
P3 Resolution: )()( fdfd  iff ),(),( AAAA hgdhgd  iff ),(),( AAAA hghg  RR
TT
if gg  and hh  for hg  i.e. if gg  and hh  for hg  .if AA gg  and AA hh  for AA hg  i.e. if AA gg  and AA hh  for AA hg  .
or
if AA gg  and AA hh  for AA gh  i.e. if AA gg  and AA hh  for AA gh 
P4 Symmetry: ),(),( AAAA ghdhgd  ie. )()( AAAA g,hh,g RR
TT  .
P5 Valuation: )()()()( fdfdffdffd 
i.e f and f  can exchange intutionistic fuzziness at various points
without affecting the sum of the degrees of intutionistic fuzziness.
15

16. Lemma 3.1 Let }...,,,{ 21 nxxxX  . A measure of fuzziness ]1,0[]1,0[]1,0[:  XX
d
satisfies valuation property iff. there exists a map ]1,0[]1,0[]1,0[:  such that
.]1,0[]1,0[))(),(()(
1
XX
n
i
iAiA fxhxgfd 
 (2)
Lemma 3.2 Let }...,,,{ 21 nxxxX  and suppose that ]1,0[]1,0[]1,0[:  XX
d is
given by (2) for some ]1,0[]1,0[]1,0[:  . Then
(a) d satisfies P1 iff. 0)1,0()0,1(  and ).1,0(,0),(  yxyx
(b) d satisfies P2 iff. yx  ].1,0[,  yx(b) d satisfies P2 iff. yx  ].1,0[,  yx
(c) d satisfies P3 iff. ),(),( txzy   , if ,tzyx  for all x, y, z, t [0, 1].
(d) d satisfies P4 iff. ),(),( xyyx   ].1,0[,  yx
Theorem 3.1 Let }...,,,{ 21 nxxxX  and suppose that ]1,0[]1,0[]1,0[:  XX
d . Then
d satisfies P1-P5, iff. d is given by (2) for some map ]1,0[]1,0[]1,0[: 
satisfying conditions (a)-(d) if lemma 3.2.
16

17. Here, it is evident that the desirable function ]1,0[]1,0[]1,0[:  in lemma
3.1 and lemma 3.2 is a restricted equivalence function. Thus, the
knowledge of a restricted equivalence function gives an entropy measure
of intutionistic fuzzy sets.
In earlier studies, entropy measures of intutionstic fuzzy sets have been
defined using certain set of axioms. A well accepted set of axioms to
define an entropy measure of intutionistic fuzzy set given by [Szmidt
and Kacprzyk, 2001].and Kacprzyk, 2001].
17

18. [Szmidt and Kacprzyk, 2001] suggested an axiomatic definition of entropy of
IFE :
Definition 3.1[Szmidt and Kacprzyk, 2001] An entropy on ),(XIF the set of
all intutionistic fuzzy sets on X is a real valued functional ],1,0[)(: XIFE
satisfying the following axiomatic requirements:
IFE1: 0)( AE iff A is a crisp set, i.e. 0)( iA xg or 1)( iA xg for all .Xxi 
IFE2: 0)( AE iff )()( iAiA xhxg  for all .Xxi 
IFE3: )()( BEAE  if BA  i.e. )()( iBiA xgxg  and ),()( iBiA xhxh  for )()( iBiB xhxg IFE3: )()( BEAE  if BA  i.e. )()( iBiA xgxg  and ),()( iBiA xhxh  for )()( iBiB xhxg 
or )()( iBiA xgxg  and ),()( iBiA xhxh  for )()( iBiB xhxg  for any .Xxi 
IFE4: ).()( c
AEAE 
In the next section, some examples of restricted equivalence and hence new
measures of intutionistic fuzzy entropy have been presented.
18

19. 4.Some examples of REF’s and new
measures of intutionistic fuzzy entropy
Some examples of REF are given as follows:
1. )1(loglog),(1 yx
yx
y
y
yx
x
xyx 




2. )1(
log
)1()1(
log
)1(
),(




xyxyyxyx
yx
19
2.
2
)1(
log
2
)1(
2
)1(
log
2
)1(
),(2




xyxyyxyx
yx
3.



















 





 

 1
4
1
4
1
)12(
1
),(3
xy
Sin
yx
Sinyx 
4.



















 





 

 1
4
1
4
1
)12(
1
),(4
xy
Cos
yx
Cosyx 

20. 5.



















 

 1
4
2
)12(
1
),(5
yx
Cosyx 
6.



















 





 







 





 

1
2
1
1
2
1
)1(
1
),( 2
1
2
1
1
6
yxyx
e
yx
e
yx
e
yx
7.    )1(2log
)1(
1
),( 11
7 yxyxyxyx 

  


20
)1( 
8.
 
)1(
1
),(
||1
8




e
e
yx
yx


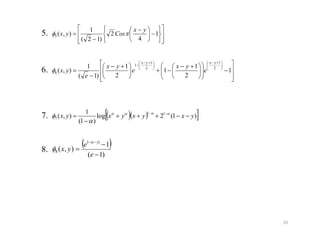
21. Measures of intutionistic fuzzy entropy corresponding to REF’s ),(1 yx
to ),(7 yx had already been studied as listed in the following table:
REF Intutionistic fuzzy entropy Author
(s)
),(1 yx








n
i iAiA
iA
iA
iAiA
iA
iA
xhxg
xh
xh
xhxg
xg
xg
n
AE
1
1
)()(
)(
log)(
)()(
)(
log)(
1
)(
)( iA x
[Vlachos
and
Sergiadas
2007]
),(2 yx





 



 

n
xhxgxhxg )(1)()(1)(1 [Zhang
21
),(2 yx









 





 

n
i
iAiAiAiA xhxgxhxg
n
AE
1
2
2
)(1)(
log
2
)(1)(1
)(








 





 

2
)(1)(
log
2
)(1)( iAiAiAiA xgxhxgxh
[Zhang
and Jiang,
2008]
),(3 yx









 


n
i
iAiA xhxg
Sin
n
AE
1
3
2
)(1)(
12
11
)( 








 

2
)(1)( iAiA xgxh
Sin
[Ye,2010]

22. ),(4 yx









 


n
i
iAiA xhxg
Cos
n
AE
1
4
2
)(1)(
12
11
)( 








 
2
)(1)( iAiA xgxh
Cos
[Ye,2010]
),(5 yx
 


















 


n
i
iAiA xhxg
Cos
n
AE
1
5 1
2
)()(
2
12
11
)( 
[Wei et
al., 2012]
),(6 yx 












 









 


2
)(1)(
1
6
2
)(1)(
)1(
11
)(
iAiA xhxg
n
i
iAiA
e
xhxg
en
AE
[Verma
and
Sharma,
22









 














 
2
)(1)(
2
)(1)(
iAiA xgxh
iAiA
e
xgxh
Sharma,
2013]
),(7 yx
   ))((2)()()()(log
)1(
1
)( 11
7 iAiAiAiAiA xxhxgxhxg
n
AE 

 



.1,0  
[Verma
and
Sharma,
2014]

23. Now, we propose a new measure of intutionistic fuzzy entropy using REF
),(8 yx
 




n
i
xhxg iAiA
e
en
AE
1
|)()(|1
1
)1(
1
)( (4)
In order for (4), to be qualified as a suitable measure of intutionistic fuzzy
entropy, it must satisfy the set IFE1-IFE4 of axiomatic requirements. In this
paper, it has been proved that (4) satisfies IFE1-IFE4.
23
paper, it has been proved that (4) satisfies IFE1-IFE4.

24. 5. Concluding Remarks
In this communication, the study of intutionistic fuzzy information measure
has been done in light of a newly defined special T-Norm and restricted
equivalence function. It has been established that the knowledge of a REF
give rise to a new intutionistic information measure. Further, a new
intutionistic fuzzy information measure have been proposed. The validity of
this measures has been tested axiomatically.
24

25. References
[1] Atanassov, K. T., Intutionistic fuzzy sets, Fuzzy Set and Systems, 20
(1986), 87-96.
[2] Bustince, H., Barrenechea, E., Pagola M., Restricted equivalence
functions, Fuzzy sets and Systems, 157 (2006), 2333 -2346.
[3] De Luca, A. and Termini, S., A definition of non-probabilistic entropy
in the settings of fuzzy set theory, Information and Control, 20(1971),
25
in the settings of fuzzy set theory, Information and Control, 20(1971),
301-312.
[4] Ebanks, B. R., On measures of fuzziness and their representations,
J.Math Anal. and Appl. ,94(1993), 24-37.
[5] Schweizer, B., and Sklar, A., Statistical metric spaces, Pacific J. of
Mathematics, 10(1960), 313-334.
[6] Shannon, C.E., The mathematical theory of communications, Bell
Syst. Tech. Journal, 27(1948), 423–467.

26. [7] Szmidt, E. and Kacprzyk, J., Entropy of intutionistic fuzzy sets, Fuzzy
sets and Systems, 118 (2001), 467 -477.
[8] Verma, R. K., and Sharma, B. D., Exponential entropy of intutionistic
fuzzy sets, Kybernetika, 49(2013), No. 1, 114-127.
[9] Verma, R. K., and Sharma, B. D., On intutionistic fuzzy entropy of
order-α, Advances in Fuzzy Systems, Volume 2014, Article ID 789890.
[10] Vlachos, I. K., Sergiadis, G. D., Intutionistic fuzzy information-
26
Applications to pattern recognition, Pattern Recognition Letters, 28
(2007), 197 -206.
[11] Wei, C.P., Gao, Z. H., and Guo, T. T., An intuitionistic fuzzy entropy
measure based on the trigonometric function, Control and Decision, 27
(2012), 4, 571–574.
[12] Ye, J., Two effective measures of intuitionistic fuzzy entropy.
Computing 87 (2010), 1–2.

27. [13] Zadeh, L. A., Fuzzy Sets, Information and control, 8 (1965), 338 -
353.
[14] Zhang, Q. S. and Jiang, S. Y., A note on information entropy
measure for vague sets. Inform. Sci. 178 (2008), 21, 4184–4191.
27

28. 28