This document provides an overview of fuzzy logic, highlighting the distinction between classical logic and fuzzy set theory. It discusses the principles of fuzzy sets, their operations, fuzzy relations, and the process of fuzzy inference, including fuzzification and defuzzification. The document emphasizes the use of fuzzy logic in reasoning and decision-making, particularly in situations involving uncertainty and linguistic terms.

1. Intelligent Computing
(MIT 554)
Unit 3: Fuzzy Logic
1

2. Natural Language and Formal Models
• Classical logic and mathematics assume that we can assign one of the two
values, true or false, to each logical proposition or statement
• Human beings are able to assimilate easily linguistic information without
thinking in any type of formalization of the specific situation
• For example, a person will have no problems to accelerate slowly while
starting a car, if he is asked to do so
• If we want to automate this action, it will not be clear at all, how to
translate this advice into a well-defined control action
• Therefore, automated control is usually not based on a linguistic
description of heuristic knowledge or knowledge from one’s own
experience, but it is based on a formal model of the technical or physical
system
2

3. Natural Language and Formal Models…
• A different technique is to use knowledge formulated in natural
language directly for the design of the control strategy
• In this case, a main problem will be the translation of the verbal
description into concrete values
• i.e., assigning “step on the gas slowly” into “step on the gas at the
velocity of a centimeter per second”
3

4. Fuzzy Set
• Classical set theory allows the membership of the elements in the set in binary terms
• Fuzzy set theory permits membership function valued in the interval [0, 1]
• Example
• Words like tall, young, rich are fuzzy
• There is no quantitative value that define the term rich
• For some people millionaire is rich, and some people billionaire is rich
• In real world there exist much fuzzy knowledge
• Human thinking and reasoning frequently involves fuzzy information
• Like answering the question in examination, which are probably true
4

5. Fuzzy Set (Membership function)…
• The membership function fully defines the fuzzy set
• A membership function provides a measure of the degree of the similarity of an
element to a fuzzy set
• Each element in the universal set U has a degree of membership, which is a real number
between 0 and 1 (including 0 and 1), in a fuzzy set S
• The fuzzy set S is denoted by listing the elements with their degrees of membership
• elements with 0 degree of membership are not included
• elements with 1 degree of membership are fully included
• elements with 0 < degree of membership <1 are partially included
• Suppose that R is the set of rich people with R = {0.4 Alice, 0.8 Brian, 0.2 Fred, 0.9 Oscar,
0.7 Rita}.
• i.e Oscar is the richest person and Fred is the poorest person among these four people
5

6. Fuzzy Set…..
• Formal Definition
• If X is universe of discourse and a is a particular element of X, then a fuzzy set
B defined on X and can be written as a collection of ordered pairs
B = {a, (a), a  X}
• Example
• Universe of discourse → CSIT students of PMC
• G → set of good students
• B → set of bad students
• G = {(Ram, 0.9), (Hari, 0.7), (Sam, 0.4)}
• D = {(Ram, 0.1), (Hari, 0.3), (Sam, 0.6)}
6

7. Fuzzy Set Operations
• Union
• The union of two fuzzy sets S and T is the fuzzy set S ∪ T, where the degree of membership
of an element in S ∪ T is the maximum of the degrees of membership of this element in S
and in T
• ST(x) = max(S(x), T(x))
• Intersection
• The intersection of two fuzzy sets S and T is the fuzzy set S ∩ T, where the degree of
membership of an element in S ∩ T is the minimum of the degrees of membership of this
element in S and in T
• ST(x) = min(S(x), T(x))
• Complement
• The complement of a fuzzy set S is the set S, with the degree of the membership of an
element in S equal to 1 minus the degree of membership of this element in S
• S(x) = 1 - S(x)
7

8. Fuzzy Set Operations……
• Example (Union)
8
Max

9. Fuzzy Set Operations……
• Example (Intersection)
9

10. Fuzzy Set Operations……
10

11. Fuzzy Set Operations……
• Exercise
• Let,
• Set of Rich People (R) = {0.4 Alice, 0.8 Brian, 0.2 Fred, 0.9 Oscar, 0.7 Rita}
• Set of Famous People (F) = {0.6 Alice, 0.9 Brian, 0.4 Fred, 0.1 Oscar, 0.5 Rita}
• Find the fuzzy set F ∪ R of rich or famous people
• Find the fuzzy set F ∩ R of rich and famous people
• Find Fc (the fuzzy set of people who are not famous) and Rc (the fuzzy set of
people who are not rich)
11

12. Interpretation of Fuzzy Sets
• Fuzzy Sets for Modeling Similarity
• Compare the object under consideration with one that definitely belongs to the
concept under consideration (and possibly also with one that definitely does not
belong to this concept)
• The similarity between two objects is higher, the smaller their distance
• Fuzzy Sets for Modeling Preference
• Membership degrees convey which values (or objects) should be preferred to others
• Fuzzy Sets for Modeling Possibility
• Possibility degrees represent a flexible restriction on what is the actual state with the
following convention: μ(u) = 0 means that u is rejected as impossible, μ(u) = 1 means
that u is totally possible, and the larger μ(u) is, the more plausible u is
12

13. Representations of Fuzzy Set
• Definition Based on Function
• Levels
13

14. Representations of Fuzzy Set…
• Definition Based on Function
• Fuzzy set μ is a real function taking values in the unit
interval and can be illustrated by drawing its graph
• If X is universe of discourse and a is a particular
element of X, then a fuzzy set B defined on X and can be
written as a collection of ordered pairs
B = {a, (a), a  X}
• Usually fuzzy sets are used for modeling expressions —
sometimes also called linguistic expressions in order to
emphasize the relation to natural language, e.g., “about
3,” “of middle height” or “very tall” which describe an
imprecise value or an imprecise interval
• Fuzzy sets associated with such expressions should
monotonically increase up to a certain value and
monotonically decrease from this value
• Such fuzzy sets are called convex
14

15. Extensions of Fuzzy Set Theory
• In classical fuzzy set theory a membership degree is
expressed by a real number in the unit interval
• However, in some applications experts prefer to use
linguistic expressions instead of numbers as
membership degrees
• In this situation one can use membership degrees
that are elements of a general lattice L (L-Fuzzy Set)
• The extension of fuzzy sets from the unit interval [0,
1] to a general lattice L and the operations can be
easily defined as follows
• An L-fuzzy set on the universe X is a mapping μ : X → L.
The operations on the class FL(X) of L-fuzzy sets are
defined point wise by setting
15

16. Fuzzy Logic
• Include all applications and theories where fuzzy sets or concepts are
involved
• Focuses on the field of approximate reasoning where fuzzy sets are
used and propagated within an inference mechanism as it is for
instance common in expert systems
16

17. Proposition and Truth values
• Classical propositional logic deals with the formal handling of
statements (propositions) to which one of the two truth values 1 (for
true) or 0 (for false) can be assigned
• Typical propositions, for which the formal symbols ϕ1 and ϕ2 may
stand are
• ϕ1 : Four is an even number.
• ϕ2 : 2 + 5 = 9.
17

18. Proposition and Truth values…
• The assumption that a statement is either true or false is suitable for
mathematical issues
• But for many expressions formulated in natural language such a strict separation
between true and false statements would be unrealistic
• If somebody promises to come to an appointment at 5 o’clock, his statement
would have been false, if he came one minute later
• Nobody would call him a liar, although, strictly speaking, his statement was not
true
• Even more complicated is the statement of being at a party at about 5
• The greater the difference between the arrival and 5 o’clock the “less true” the
statement is
• A sharp definition of an interval of time corresponding to “about 5” is impossible
18

19. Proposition and Truth values…
• Humans are able to formulate such “fuzzy” statements, understand
them, draw conclusions from them and work with them
• If someone starts an approximately four-hour-drive at around 11
o’clock and is going to have lunch for about half an hour, we can use
these imprecise pieces of information and conclude at what time
more or less the person will arrive
• A formalization of this simple issue in a logical calculus, where
statements can be either true or false only, is not adequate
19

20. t-Norm operator
• Triangular Norm
• Is a binary operation on the unit interval [0, 1], a function T: [0, 1] 
[0, 1]  [0, 1], such that for all a, b, c  [0, 1], the following four
axioms are satisfied
• T1 : T(a, b) = T(b, a)  Commutative Property
• T2 : T(a, T(b, c)) = T(T(a, b), c)  Associativity Property
• T3 : T(a, 1) = a  Boundary Condition
• T4 : T(a, a) = a Idempotency
• T5 : T(a, b)  T(a, c) whenever b  c  Monotonicity Property, where a, b and
c are membership functions
20

21. t-Norm operator…
1. Minimum
 Tmin(A(x),  B(x)) = min (A(x), B(x)) =  A(x)   B(x)
2. Algebraic Product
 Tap(A(x),  B(x)) =  A(x)   B(x)
3. Bounded Product
 Tbp(A(x),  B(x)) = MAX(0, (A(x) +  B(x) – 1))
4. Drastic Product
 𝑇𝑑𝑝 𝜇𝐴 𝑥 , 𝜇𝐵 𝑥 =
𝜇𝐴 𝑥 𝑖𝑓 𝜇𝐵 𝑥 = 1
𝜇𝐵 𝑥 𝑖𝑓𝜇𝐴 𝑥 = 1
0𝑖𝑓𝜇𝐴 𝑥 < 1&&𝜇𝐵(𝑥) < 1
21

22. t-Norm operator…
• Example
• A = {(a, 0.7), (b, 0.5), (c, 0.1), (d, 0.6)}
• B = {(b, 0.8), (c, 0.3)}
22

23. t-conorm operator
• Triangular conorm
• Is a binary operation on the unit interval [0, 1], a function T: [0, 1] 
[0, 1]  [0, 1], such that for all a, b, c  [0, 1], the following four
axioms are satisfied
• T1 : T(a, b) = T(b, a)  Commutative Property
• T2 : T(a, T(b, c)) = T(T(a, b), c)  Associativity Property
• T3 : T(a, 0) = a  Boundary Condition
• T4 : T(a, b)  T(a, c) whenever b  c  Monotonicity Property, where a, b and
c are membership functions
23

24. t-conorm operator…
1. Standard Union (Maximum)
 Tmax(A(x), B(x)) = max (A(x), B(x)) = A(x)   B(x)
2. Algebraic Sum
 Tas(A(x),  B(x)) =  A(x) +  B(x) -  A(x)   B(x)
3. Bounded Sum
 Tbs(A(x),  B(x)) = MIN(1, (A(x) +  B(x) ))
4. Drastic Union
 𝑇𝑑𝑝 𝜇𝐴 𝑥 , 𝜇𝐵 𝑥 =
𝜇𝐴 𝑥 𝑖𝑓 𝜇𝐵 𝑥 = 0
𝜇𝐵 𝑥 𝑖𝑓𝜇𝐴 𝑥 = 0
1𝑖𝑓𝜇𝐴 𝑥 < 1&&𝜇𝐵(𝑥) < 1
24

25. Decomposition of a Fuzzy Set
• The representation of an arbitrary fuzzy set A in terms of the special
fuzzy set A, which are defined in terms of the -cuts of A by 𝛼𝐴(𝑥) =
𝛼. 𝛼𝐴(𝑥)
• Referred as a decomposition of the fuzzy set A
• Example
• X = {a, b, c, d, e}
• Fuzzy Set (A) = {(a, 0.2), (b, 0.4), (c, 0.6), (d, 0.8), (e, 1)}
25

26. Fuzzy Relations
• Crisp Relation
26

27. Fuzzy Relations…
• A fuzzy relation R is a mapping from the Cartesian space XY to the
interval [0, 1], where the strength of the mapping is expressed by the
membership function of the relation 𝜇𝑅 𝑥, 𝑦
• Example
• A = {(x1, 0.6), (x2, 0.2), (x3, 0.3)}
• B = {(y1, 0.7), (y2, 0.3), (y3, 0.4)}
• 𝜇𝑅 𝑥, 𝑦 = 𝜇𝐴×𝐵 𝑥, 𝑦 = min{𝜇𝐴 𝑥 , 𝜇𝐵(𝑦)}
27

28. Fuzzy Inference
• Together, the fuzzy sets and fuzzy
rules form the knowledge base of a
fuzzy rule-based reasoning system
• In addition to the knowledge base, a
fuzzy reasoning system consists of
three other components, each
performing a specific task
1. Fuzzification
2. Inferencing
3. Deffuzification
28

29. Fuzzification
• Process of transforming a crisp set to a fuzzy set
• Methods of Membership value Assignments
• Intuition
• Inference
29

30. Defuzzification
• Process of transforming a fuzzy set to a crisp set
• Methods
• Lambda Cut
• Maxima Method
• Weighted Average Method
30

31. Fuzzy Data Analysis
• Fuzzy Clustering (Illustration in Class)
• Fuzzy Classifier (Illustration in Class)
31

32. Fuzzy Clustering
• Is a type of clustering algorithm in machine
learning that allows a data point to belong to
more than one cluster with different degrees
of membership
• Unlike traditional clustering algorithms, such
as k-means or hierarchical clustering, which
assign each data point to a single cluster,
fuzzy clustering assigns a membership degree
between 0 and 1 for each data point for each
cluster
• FCM (Fuzzy c-Means) Algorithm
32

33. Fuzzy Clustering…
• Fuzzy c-Means
1. Initialize the data points into the desired number of clusters randomly
2. Find out the centroid 𝑉𝑖𝑗 = 𝑘=1
𝑛
𝜇𝑖𝑘
𝑚×𝑥𝑘
𝑘=1
𝑛 𝜇𝑖𝑘
𝑚 where, m is fuzziness parameter
(2)
3. Find out the distance of each point from the centroid
4. Updating membership values 𝜇𝑘𝑖 = 𝑗=1
𝑛 𝑑𝑘𝑖
2
𝑑𝑘𝑗
2
1
𝑚−1
−1
5. Repeat the steps(2-4) until the constant values are obtained for the
membership values or the difference is less than the tolerance value
6. Defuzzify the obtained membership values
33

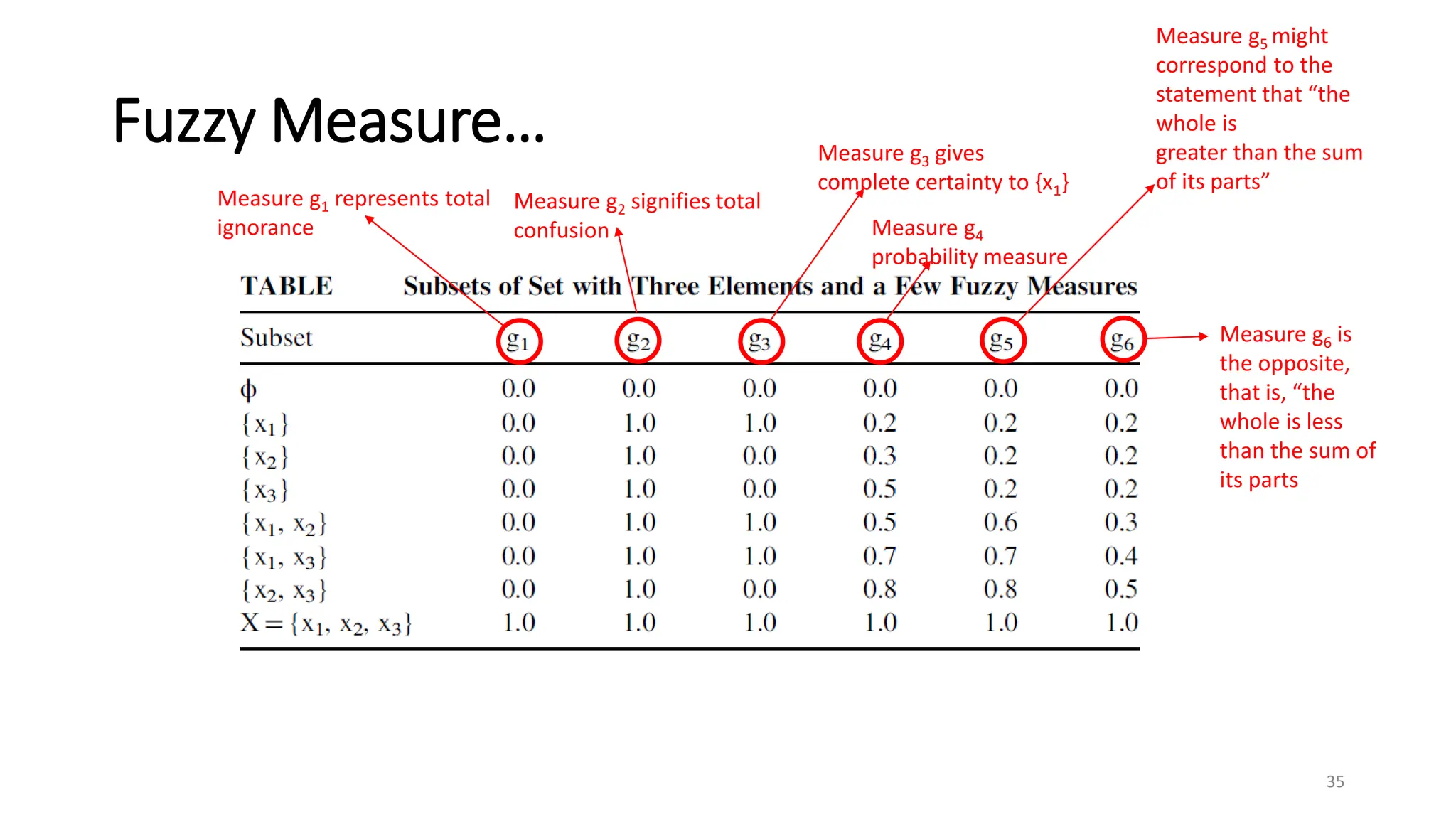
34. Fuzzy Measure
• Consider a finite set X = {x1, x2, . . . , xn}
• Each xi can be a diagnostic test, a
feature (e.g., color, texture, or shape)
in a segmentation problem, a
particular pattern recognition
algorithm, and so on
• Let 2X denote the power set of X, that
is, the set of all (crisp) subsets of X
• A fuzzy measure, g, is a real-valued
function g : 2X  [0, 1], satisfying the
following properties
1. g() = 0 and g(X) = 1
2. g(A)  g(B), if A  B
34

35. Fuzzy Measure…
35
Measure g1 represents total
ignorance
Measure g2 signifies total
confusion
Measure g3 gives
complete certainty to {x1}
Measure g4
probability measure
Measure g5 might
correspond to the
statement that “the
whole is
greater than the sum
of its parts”
Measure g6 is
the opposite,
that is, “the
whole is less
than the sum of
its parts

36. Assignment
• Fuzzy Integral
36

37. End of Unit 3
37