Uploaded byASPAK2014
PDF, PPTX1,159 views

Iterative Compression

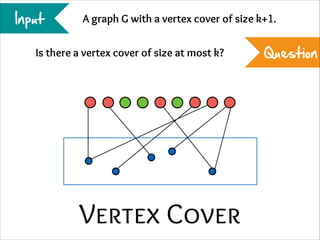
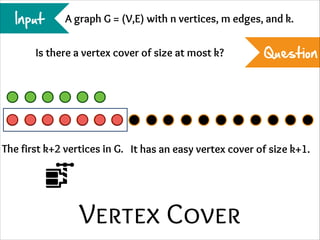
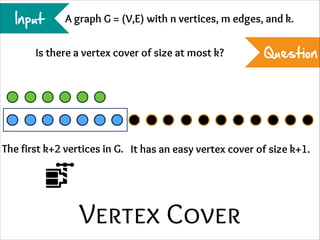
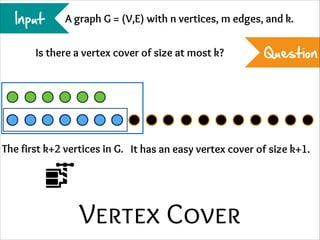
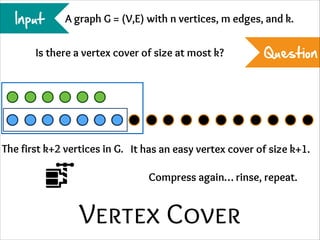
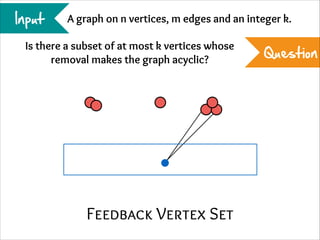
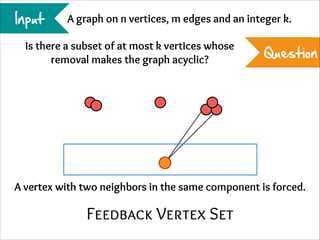
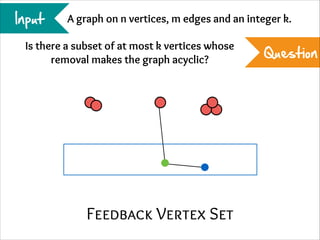
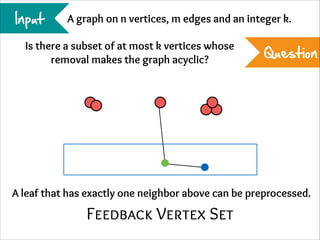
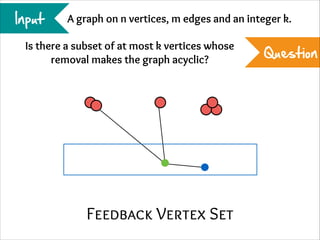
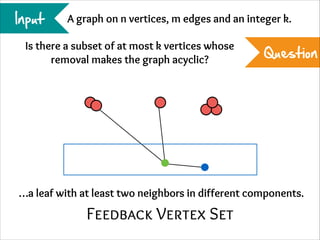
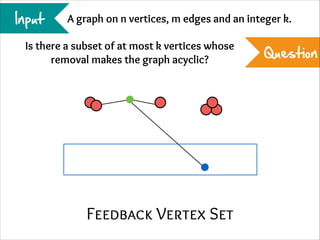
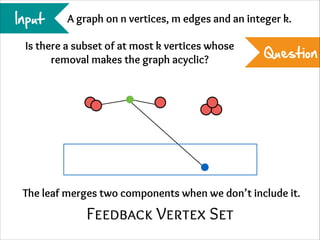
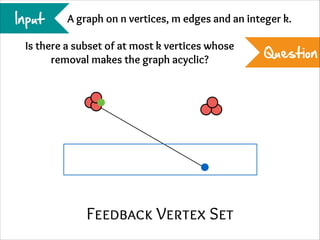
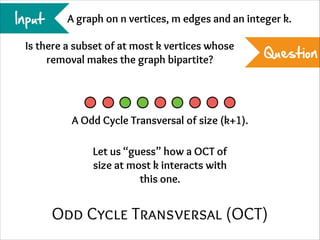
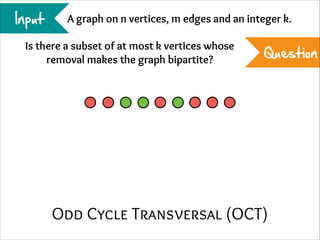
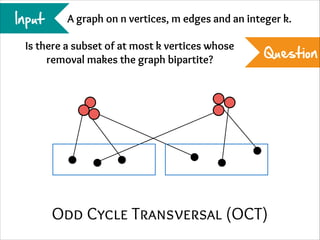
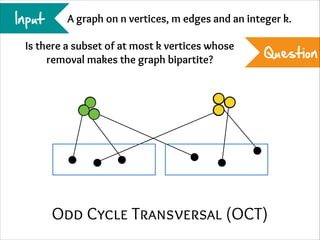
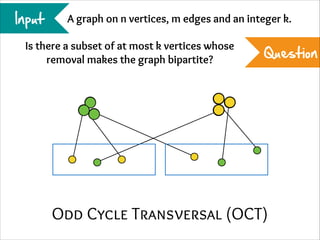
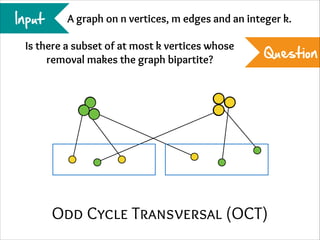
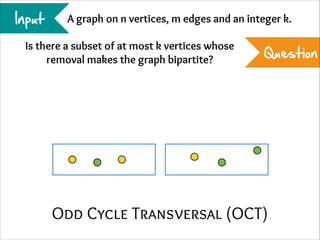
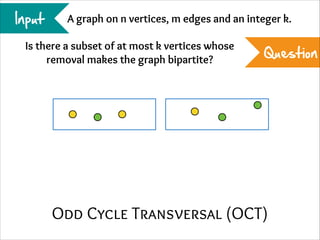
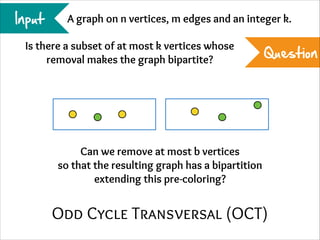
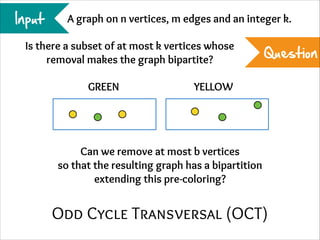
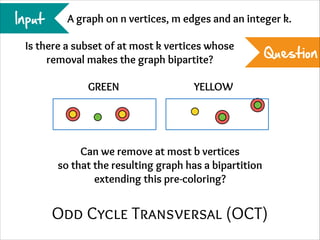
The document describes the iterative compression technique for designing fixed-parameter tractable algorithms. It shows how to use a vertex/edge cover, feedback vertex set, or odd cycle transversal of size k+1 as "compression" to design a branching algorithm with running time of O*(ck) for some constant c. This technique involves guessing how an optimal solution of size k interacts with the given size k+1 solution, and branching based on including or excluding vertices in the optimal solution.

Embed presentation

Download as PDF, PPTX
Iterative Compression
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Let us “guess” how a vertex cover of size at most k interacts with this one. Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Let us “guess” how a vertex cover of size at most k interacts with this one. Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Let us “guess” how a vertex cover of size at most k interacts with this one. Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Can there be an edge between two red vertices? Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Now we need to make up for the work that the red vertices were doing. Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? Vertex Cover Question
Input A graph G with a vertex cover of size k+1. Is there a vertex cover of size at most k? Vertex Cover Question
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? The first k+2 vertices in G. Vertex Cover Question
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Vertex Cover
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Vertex Cover
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Vertex Cover
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Vertex Cover
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Vertex Cover
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Compress again… rinse, repeat. Vertex Cover
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a subset of vertices S of size at most k that intersects all the edges? Question We have a O*(2k) algorithm for Vertex Cover. Vertex Cover
Input A graph G = (V,E) with n vertices, m edges, and k. Is there a subset of vertices S of size at most k that intersects all the edges? Question We have a O*(2k) algorithm for Vertex Cover. Vertex Cover
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? A Feedback Vertex Set of size (k+1). Let us “guess” how a FVS of size at most k interacts with this one. Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question A vertex with two neighbors in the same component is forced. Feedback Vertex Set
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question A leaf that has exactly one neighbor above can be preprocessed. Feedback Vertex Set
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question …a leaf with at least two neighbors in different components. Feedback Vertex Set
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question The leaf merges two components when we don’t include it. Feedback Vertex Set
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question The number of components “on top” decreases. Feedback Vertex Set
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question Start with a leaf. ! Two neighbors in one component: forced. At most one neighbor above: preprocess. At least two neighbors, all in different components above: branch. Feedback Vertex Set
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question Let t denote the number of components among the red vertices. Let w = (k+t). Feedback Vertex Set
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question Let t denote the number of components among the red vertices. Let w = (k+t). Include v… k drops by 1 Exclude v… t drops by at least 1 Feedback Vertex Set
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question Let t denote the number of components among the red vertices. Let w = (k+t). Include v… k drops by 1 Exclude v… t drops by at least 1 Either way, w drops by at least one. Feedback Vertex Set
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Either way, w drops by at least one. Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Either way, w drops by at least one. Running time: 2w = 2(k+t) Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Either way, w drops by at least one. Running time: 2w = 2(k+t) ≤ 2k+k ≤ 4k Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Either way, w drops by at least one. Running time: 2w = 2(k+t) ≤ 2k+k ≤ 4k Overall Running Time… Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Either way, w drops by at least one. Running time: 2w = 2(k+t) ≤ 2k+k ≤ 4k Overall Running Time… k i=1 k k k 4 =5 i Feedback Vertex Set Question
Input A tournament T on n vertices and an integer k. Is there a subset of k arcs that can be reversed to make the tournament acyclic? This implies an O(5k) algorithm for FVS. Feedback Vertex Set Question
Input A tournament T on n vertices and an integer k. Is there a subset of k arcs that can be reversed to make the tournament acyclic? This implies an O(5k) algorithm for FVS. Feedback Vertex Set Question
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question A Odd Cycle Transversal of size (k+1). Let us “guess” how a OCT of size at most k interacts with this one. Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Can we remove at most b vertices so that the resulting graph has a bipartition extending this pre-coloring? Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? GREEN Question YELLOW Can we remove at most b vertices so that the resulting graph has a bipartition extending this pre-coloring? Odd Cycle Transversal (OCT)
Input A graph on n vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? GREEN Question YELLOW Can we remove at most b vertices so that the resulting graph has a bipartition extending this pre-coloring? Odd Cycle Transversal (OCT)
Input A tournament T on n vertices and an integer k. Is there a subset of k arcs that can be reversed to make the tournament acyclic? Question This implies an O*(3k) algorithm for OCT. Odd Cycle Transversal (OCT)
Input A tournament T on n vertices and an integer k. Is there a subset of k arcs that can be reversed to make the tournament acyclic? Question This implies an O*(3k) algorithm for OCT. Odd Cycle Transversal (OCT)
Take Away…
Show that the problem has a hereditary property Solve the “compression” question, or even a “Disjoint” version.
Show that the problem has a hereditary property Solve the “compression” question, or even a “Disjoint” version. Is a framework that can be setup quite easily.
Show that the problem has a hereditary property Solve the “compression” question, or even a “Disjoint” version. Is a framework that can be setup quite easily. The compression algorithm can be fairly non-trivial.

More Related Content

PPT
lecture 30
bysajinsc
 
PDF
Efficient Simplification: The (im)possibilities
byNeeldhara Misra
 
PDF
Steiner Tree Parameterized by Treewidth
byASPAK2014
 
PDF
EKR for Matchings
byNeeldhara Misra
 
PDF
Kernels for Planar F-Deletion (Restricted Variants)
byNeeldhara Misra
 
PDF
From FVS to F-Deletion
byNeeldhara Misra
 
PDF
A Kernel for Planar F-deletion: The Connected Case
byNeeldhara Misra
 
PDF
Separators with Non-Hereditary Properties
byNeeldhara Misra
 
lecture 30
bysajinsc
 
Efficient Simplification: The (im)possibilities
byNeeldhara Misra
 
Steiner Tree Parameterized by Treewidth
byASPAK2014
 
EKR for Matchings
byNeeldhara Misra
 
Kernels for Planar F-Deletion (Restricted Variants)
byNeeldhara Misra
 
From FVS to F-Deletion
byNeeldhara Misra
 
A Kernel for Planar F-deletion: The Connected Case
byNeeldhara Misra
 
Separators with Non-Hereditary Properties
byNeeldhara Misra
 

Viewers also liked

PDF
Graph Modification Algorithms
byNeeldhara Misra
 
PDF
Lower Bounds In Kernelization
byNeeldhara Misra
 
PDF
Important Cuts and (p,q)-clustering
byASPAK2014
 
PDF
Treewidth and Applications
byASPAK2014
 
PDF
Important Cuts
byASPAK2014
 
PDF
Bidimensionality
byASPAK2014
 
PDF
Kernel Lower Bounds
byASPAK2014
 
PDF
The Exponential Time Hypothesis
byASPAK2014
 
PDF
Cut and Count
byASPAK2014
 
PDF
Representative Sets
byASPAK2014
 
PDF
Kernelization Basics
byASPAK2014
 
PDF
Fixed-Parameter Intractability
byASPAK2014
 
PDF
Paths and Polynomials
byASPAK2014
 
PDF
Matroid Basics
byASPAK2014
 
PDF
Color Coding
byASPAK2014
 
PDF
Dynamic Programming Over Graphs of Bounded Treewidth
byASPAK2014
 
Graph Modification Algorithms
byNeeldhara Misra
 
Lower Bounds In Kernelization
byNeeldhara Misra
 
Important Cuts and (p,q)-clustering
byASPAK2014
 
Treewidth and Applications
byASPAK2014
 
Important Cuts
byASPAK2014
 
Bidimensionality
byASPAK2014
 
Kernel Lower Bounds
byASPAK2014
 
The Exponential Time Hypothesis
byASPAK2014
 
Cut and Count
byASPAK2014
 
Representative Sets
byASPAK2014
 
Kernelization Basics
byASPAK2014
 
Fixed-Parameter Intractability
byASPAK2014
 
Paths and Polynomials
byASPAK2014
 
Matroid Basics
byASPAK2014
 
Color Coding
byASPAK2014
 
Dynamic Programming Over Graphs of Bounded Treewidth
byASPAK2014
 

Similar to Iterative Compression

PPT
Mathematics classes and pptPPT-Graphs.ppt
bykakash77897
 
PPT
PPT-graph-Graphs-theory-notes-introduction
byvanaj123
 
DOCX
Cs6660 compiler design november december 2016 Answer key
byappasami
 
PDF
Graph Modification Problems: A Modern Perspective
byNeeldhara Misra
 
PPTX
Algorithms Design Exam Help
byProgramming Exam Help
 
PPTX
Algorithms Design Assignment Help
byProgramming Homework Help
 
PPTX
NP Complete Problems -- Internship
bySeshagiri Rao Kornepati
 
PDF
Expansions for Reductions
byNeeldhara Misra
 
PPT
Chap11alg
byMunhchimeg
 
PPT
Chap11alg
byMunkhchimeg
 
PDF
Solutions1.1
byPraveen Kumar
 
PDF
Introduction to Treewidth
byASPAK2014
 
PDF
ACM ICPC 2013 NEERC (Northeastern European Regional Contest) Problems Review
byRoman Elizarov
 
PDF
Connected Dominating Set and Short Cycles
byNeeldhara Misra
 
DOC
Question bank
bychandrashekardk
 
PPTX
ICPC 2015, Tsukuba : Unofficial Commentary
byirrrrr
 
PPT
Giáo trình Phân tích và thiết kế giải thuật - CHAP 8
byNguyễn Công Hoàng
 
PDF
solved-question-paper-questions-graph-theory1 (1).pdf
bymeghum5287
 
PDF
Ejercicios propuestos Estructuras Discretas II Verónica Torres
byVeronica Torres
 
PDF
Polynomial Kernel for Interval Vertex Deletion
byAkankshaAgrawal55
 
Mathematics classes and pptPPT-Graphs.ppt
bykakash77897
 
PPT-graph-Graphs-theory-notes-introduction
byvanaj123
 
Cs6660 compiler design november december 2016 Answer key
byappasami
 
Graph Modification Problems: A Modern Perspective
byNeeldhara Misra
 
Algorithms Design Exam Help
byProgramming Exam Help
 
Algorithms Design Assignment Help
byProgramming Homework Help
 
NP Complete Problems -- Internship
bySeshagiri Rao Kornepati
 
Expansions for Reductions
byNeeldhara Misra
 
Chap11alg
byMunhchimeg
 
Chap11alg
byMunkhchimeg
 
Solutions1.1
byPraveen Kumar
 
Introduction to Treewidth
byASPAK2014
 
ACM ICPC 2013 NEERC (Northeastern European Regional Contest) Problems Review
byRoman Elizarov
 
Connected Dominating Set and Short Cycles
byNeeldhara Misra
 
Question bank
bychandrashekardk
 
ICPC 2015, Tsukuba : Unofficial Commentary
byirrrrr
 
Giáo trình Phân tích và thiết kế giải thuật - CHAP 8
byNguyễn Công Hoàng
 
solved-question-paper-questions-graph-theory1 (1).pdf
bymeghum5287
 
Ejercicios propuestos Estructuras Discretas II Verónica Torres
byVeronica Torres
 
Polynomial Kernel for Interval Vertex Deletion
byAkankshaAgrawal55
 

Recently uploaded

PDF
Deploying Windows Clients & Managing Identities
byVICTOR MAESTRE RAMIREZ
 
PDF
Safer’s Picks: Recent FME Enhancements with Big Everyday Impact
bySafe Software
 
PDF
Smart Cloud Solutions-Smart,Secure & Scalable
byfloydjsmith02
 
PPTX
Advance Computer Architecture Lecture 4.pptx
byBottshikanBottshikan
 
PDF
TopMate ES11 3-Wheel Electric Scooter: Comfortable, Stable Mobility for Every...
byTopmate
 
PPTX
Migrating-Hadoop-to-Databricks-Ebook-FINAL.pptx
byssuserf37fc8
 
PDF
Talaria: A Sound-Driven Music Search Engine for Discovery Beyond Metadata
byShuen-Huei Guan
 
PPTX
AI Meets DBA Transforming Database Administration with Intelligence
byGeoPITS Global Pvt Ltd
 
PPTX
Achieve enterprise automation with SAP BTP solutions and SAP Signavio
bydarrellkiwi
 
PPTX
Apache Kafka 101 for Techies in IT dep.pptx
byamulyareddyk97
 
PPTX
Storage-and-HCI-Positioning-update-sales.pptx
byhungungphu123
 
PDF
How to Build a Crypto Wallet that Excels in 2026.pdf
byimoliviabennett
 
PDF
Lightweight, Travel-Ready Freedom for Adults and Seniors
byTopmate
 
PDF
Unlocking Gen AI Capabilities Within UiPath Document Understanding
byDianaGray10
 
PPTX
API Gateway Architecture - Technical Report 2026
byPowersoft2026
 
PPTX
Mastering SQL Server Replication: Types, Setup & Troubleshooting
byGeoPITS Global Pvt Ltd
 
PPTX
Understanding-Search-Algorithms_09-12-25.pptx
byshaikmahammedtauheed
 
PPTX
apidays Australia 2025 | Building AI RAG Applications with No Code.pptx
byapidays
 
PPTX
The Abomination of AI – keynote at ICoSCI 2026
byAlan Dix
 
PDF
Ethical AI applied to publishing: Presenting wâsikan kisewâtisiwin, an AI too...
byBookNet Canada
 
Deploying Windows Clients & Managing Identities
byVICTOR MAESTRE RAMIREZ
 
Safer’s Picks: Recent FME Enhancements with Big Everyday Impact
bySafe Software
 
Smart Cloud Solutions-Smart,Secure & Scalable
byfloydjsmith02
 
Advance Computer Architecture Lecture 4.pptx
byBottshikanBottshikan
 
TopMate ES11 3-Wheel Electric Scooter: Comfortable, Stable Mobility for Every...
byTopmate
 
Migrating-Hadoop-to-Databricks-Ebook-FINAL.pptx
byssuserf37fc8
 
Talaria: A Sound-Driven Music Search Engine for Discovery Beyond Metadata
byShuen-Huei Guan
 
AI Meets DBA Transforming Database Administration with Intelligence
byGeoPITS Global Pvt Ltd
 
Achieve enterprise automation with SAP BTP solutions and SAP Signavio
bydarrellkiwi
 
Apache Kafka 101 for Techies in IT dep.pptx
byamulyareddyk97
 
Storage-and-HCI-Positioning-update-sales.pptx
byhungungphu123
 
How to Build a Crypto Wallet that Excels in 2026.pdf
byimoliviabennett
 
Lightweight, Travel-Ready Freedom for Adults and Seniors
byTopmate
 
Unlocking Gen AI Capabilities Within UiPath Document Understanding
byDianaGray10
 
API Gateway Architecture - Technical Report 2026
byPowersoft2026
 
Mastering SQL Server Replication: Types, Setup & Troubleshooting
byGeoPITS Global Pvt Ltd
 
Understanding-Search-Algorithms_09-12-25.pptx
byshaikmahammedtauheed
 
apidays Australia 2025 | Building AI RAG Applications with No Code.pptx
byapidays
 
The Abomination of AI – keynote at ICoSCI 2026
byAlan Dix
 
Ethical AI applied to publishing: Presenting wâsikan kisewâtisiwin, an AI too...
byBookNet Canada
 

Iterative Compression

  • 1.
  • 2.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
  • 3.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
  • 4.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Vertex Cover Question
  • 5.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Vertex Cover Question
  • 6.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Vertex Cover Question
  • 7.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Let us “guess” how a vertex cover of size at most k interacts with this one. Vertex Cover Question
  • 8.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Let us “guess” how a vertex cover of size at most k interacts with this one. Vertex Cover Question
  • 9.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Let us “guess” how a vertex cover of size at most k interacts with this one. Vertex Cover Question
  • 10.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Vertex Cover Question
  • 11.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Can there be an edge between two red vertices? Vertex Cover Question
  • 12.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Vertex Cover Question
  • 13.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? A vertex cover of size (k+1). Now we need to make up for the work that the red vertices were doing. Vertex Cover Question
  • 14.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? Vertex Cover Question
  • 15.
    Input A graph Gwith a vertex cover of size k+1. Is there a vertex cover of size at most k? Vertex Cover Question
  • 16.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
  • 17.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
  • 18.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
  • 19.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Vertex Cover Question
  • 20.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? The first k+2 vertices in G. Vertex Cover Question
  • 21.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Vertex Cover
  • 22.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Vertex Cover
  • 23.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Vertex Cover
  • 24.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Vertex Cover
  • 25.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Vertex Cover
  • 26.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a vertex cover of size at most k? Question The first k+2 vertices in G. It has an easy vertex cover of size k+1. Compress again… rinse, repeat. Vertex Cover
  • 27.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a subset of vertices S of size at most k that intersects all the edges? Question We have a O*(2k) algorithm for Vertex Cover. Vertex Cover
  • 28.
    Input A graph G= (V,E) with n vertices, m edges, and k. Is there a subset of vertices S of size at most k that intersects all the edges? Question We have a O*(2k) algorithm for Vertex Cover. Vertex Cover
  • 29.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? A Feedback Vertex Set of size (k+1). Let us “guess” how a FVS of size at most k interacts with this one. Feedback Vertex Set Question
  • 30.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
  • 31.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
  • 32.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
  • 33.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
  • 34.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question A vertex with two neighbors in the same component is forced. Feedback Vertex Set
  • 35.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
  • 36.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question A leaf that has exactly one neighbor above can be preprocessed. Feedback Vertex Set
  • 37.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
  • 38.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question …a leaf with at least two neighbors in different components. Feedback Vertex Set
  • 39.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
  • 40.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question The leaf merges two components when we don’t include it. Feedback Vertex Set
  • 41.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
  • 42.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question The number of components “on top” decreases. Feedback Vertex Set
  • 43.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question Start with a leaf. ! Two neighbors in one component: forced. At most one neighbor above: preprocess. At least two neighbors, all in different components above: branch. Feedback Vertex Set
  • 44.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Feedback Vertex Set Question
  • 45.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question Let t denote the number of components among the red vertices. Let w = (k+t). Feedback Vertex Set
  • 46.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question Let t denote the number of components among the red vertices. Let w = (k+t). Include v… k drops by 1 Exclude v… t drops by at least 1 Feedback Vertex Set
  • 47.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Question Let t denote the number of components among the red vertices. Let w = (k+t). Include v… k drops by 1 Exclude v… t drops by at least 1 Either way, w drops by at least one. Feedback Vertex Set
  • 48.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Either way, w drops by at least one. Feedback Vertex Set Question
  • 49.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Either way, w drops by at least one. Running time: 2w = 2(k+t) Feedback Vertex Set Question
  • 50.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Either way, w drops by at least one. Running time: 2w = 2(k+t) ≤ 2k+k ≤ 4k Feedback Vertex Set Question
  • 51.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Either way, w drops by at least one. Running time: 2w = 2(k+t) ≤ 2k+k ≤ 4k Overall Running Time… Feedback Vertex Set Question
  • 52.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph acyclic? Either way, w drops by at least one. Running time: 2w = 2(k+t) ≤ 2k+k ≤ 4k Overall Running Time… k i=1 k k k 4 =5 i Feedback Vertex Set Question
  • 53.
    Input A tournament Ton n vertices and an integer k. Is there a subset of k arcs that can be reversed to make the tournament acyclic? This implies an O(5k) algorithm for FVS. Feedback Vertex Set Question
  • 54.
    Input A tournament Ton n vertices and an integer k. Is there a subset of k arcs that can be reversed to make the tournament acyclic? This implies an O(5k) algorithm for FVS. Feedback Vertex Set Question
  • 55.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question A Odd Cycle Transversal of size (k+1). Let us “guess” how a OCT of size at most k interacts with this one. Odd Cycle Transversal (OCT)
  • 56.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
  • 57.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
  • 58.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
  • 59.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
  • 60.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
  • 61.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
  • 62.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
  • 63.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
  • 64.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
  • 65.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Odd Cycle Transversal (OCT)
  • 66.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? Question Can we remove at most b vertices so that the resulting graph has a bipartition extending this pre-coloring? Odd Cycle Transversal (OCT)
  • 67.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? GREEN Question YELLOW Can we remove at most b vertices so that the resulting graph has a bipartition extending this pre-coloring? Odd Cycle Transversal (OCT)
  • 68.
    Input A graph onn vertices, m edges and an integer k. Is there a subset of at most k vertices whose removal makes the graph bipartite? GREEN Question YELLOW Can we remove at most b vertices so that the resulting graph has a bipartition extending this pre-coloring? Odd Cycle Transversal (OCT)
  • 69.
    Input A tournament Ton n vertices and an integer k. Is there a subset of k arcs that can be reversed to make the tournament acyclic? Question This implies an O*(3k) algorithm for OCT. Odd Cycle Transversal (OCT)
  • 70.
    Input A tournament Ton n vertices and an integer k. Is there a subset of k arcs that can be reversed to make the tournament acyclic? Question This implies an O*(3k) algorithm for OCT. Odd Cycle Transversal (OCT)
  • 71.
  • 73.
    Show that the problemhas a hereditary property Solve the “compression” question, or even a “Disjoint” version.
  • 74.
    Show that the problemhas a hereditary property Solve the “compression” question, or even a “Disjoint” version. Is a framework that can be setup quite easily.
  • 75.
    Show that the problemhas a hereditary property Solve the “compression” question, or even a “Disjoint” version. Is a framework that can be setup quite easily. The compression algorithm can be fairly non-trivial.