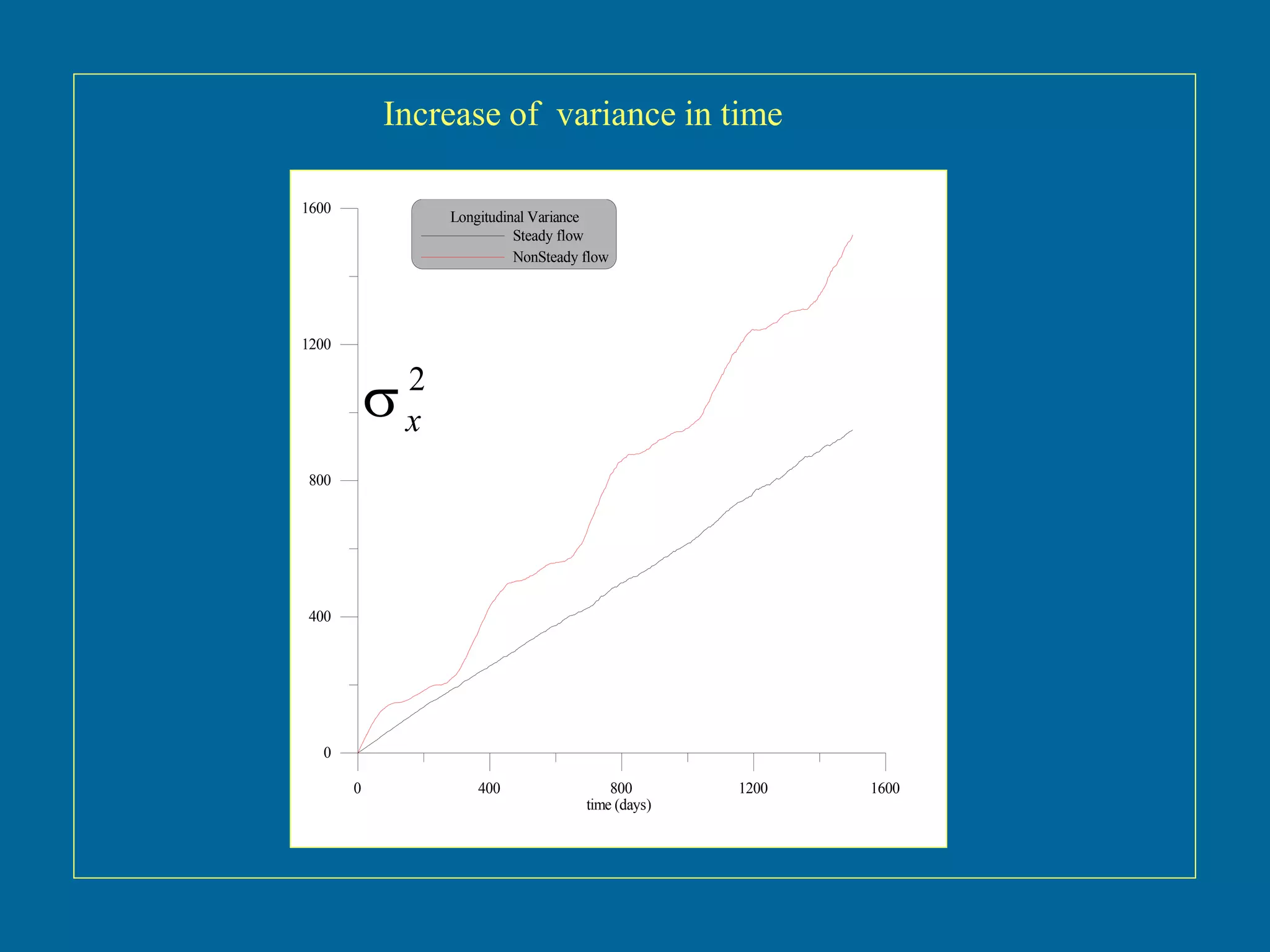
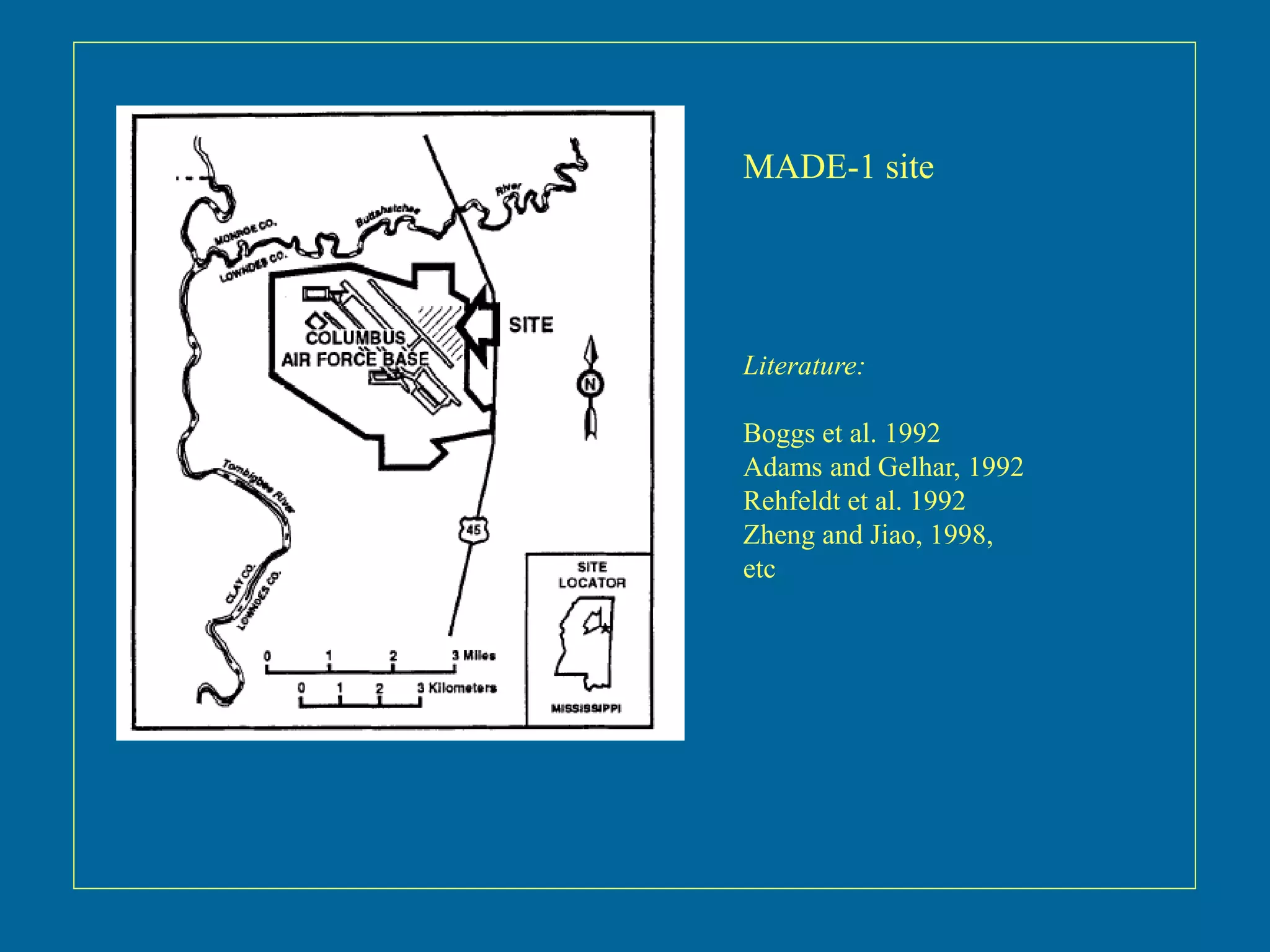
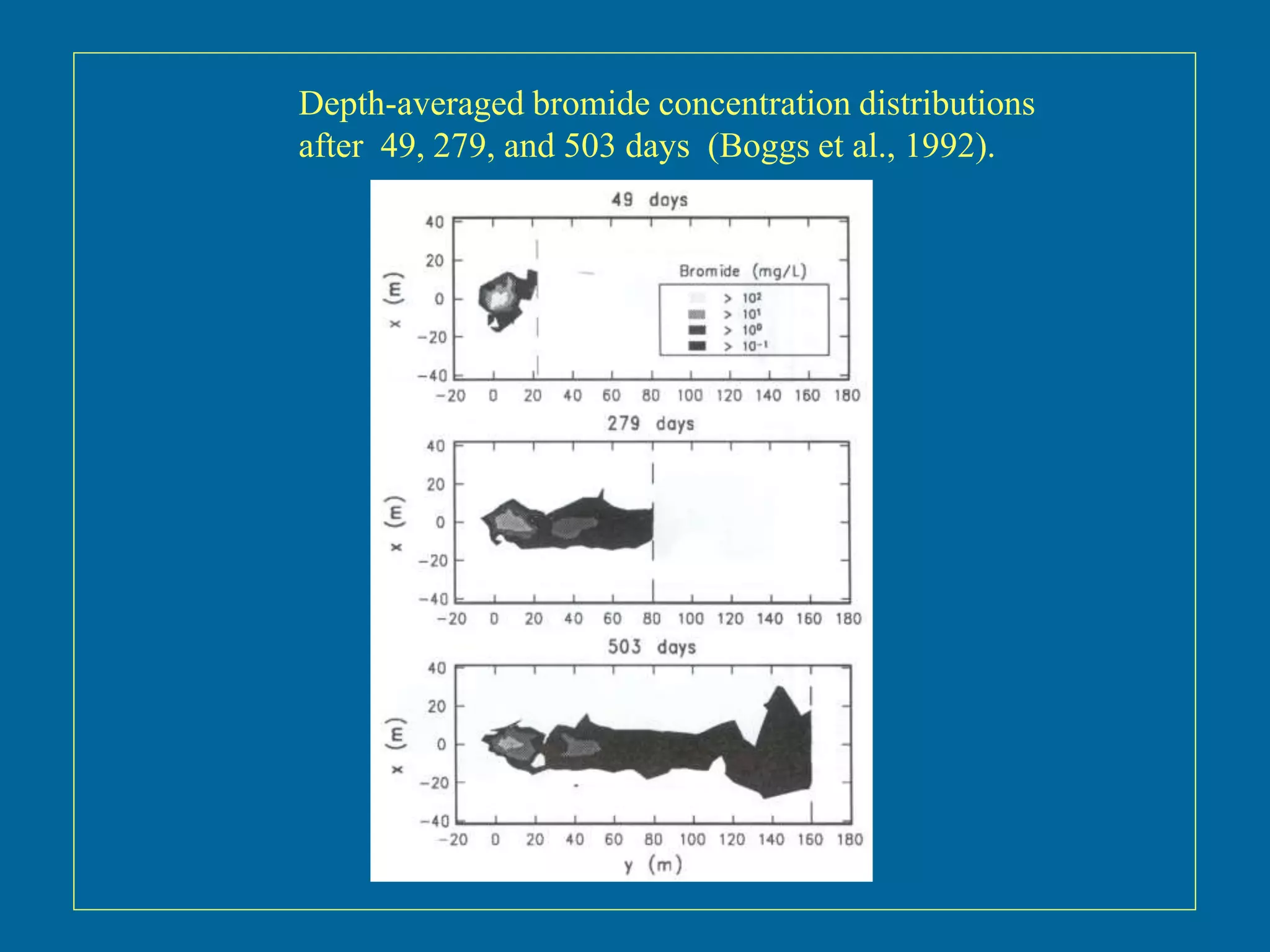
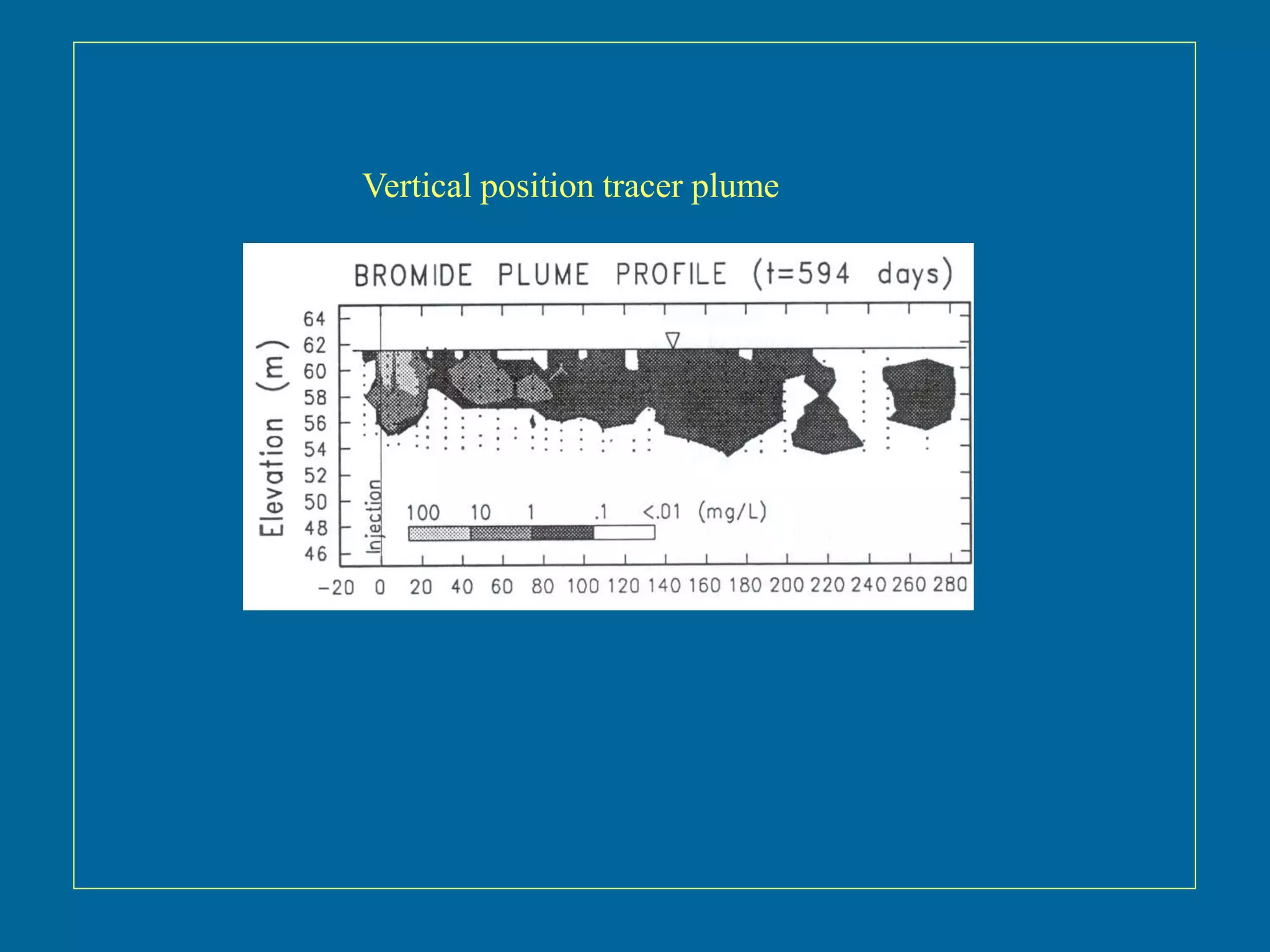
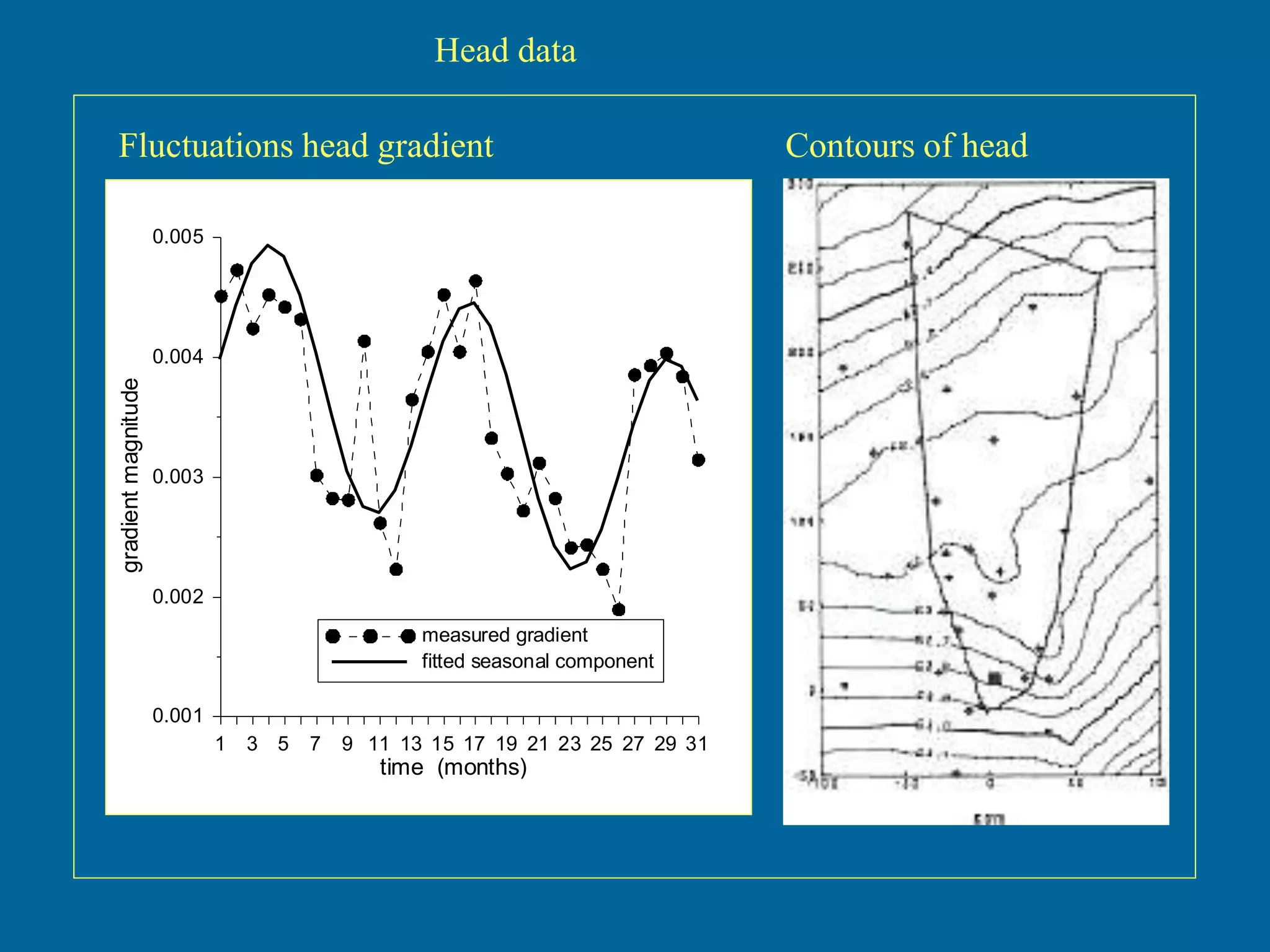
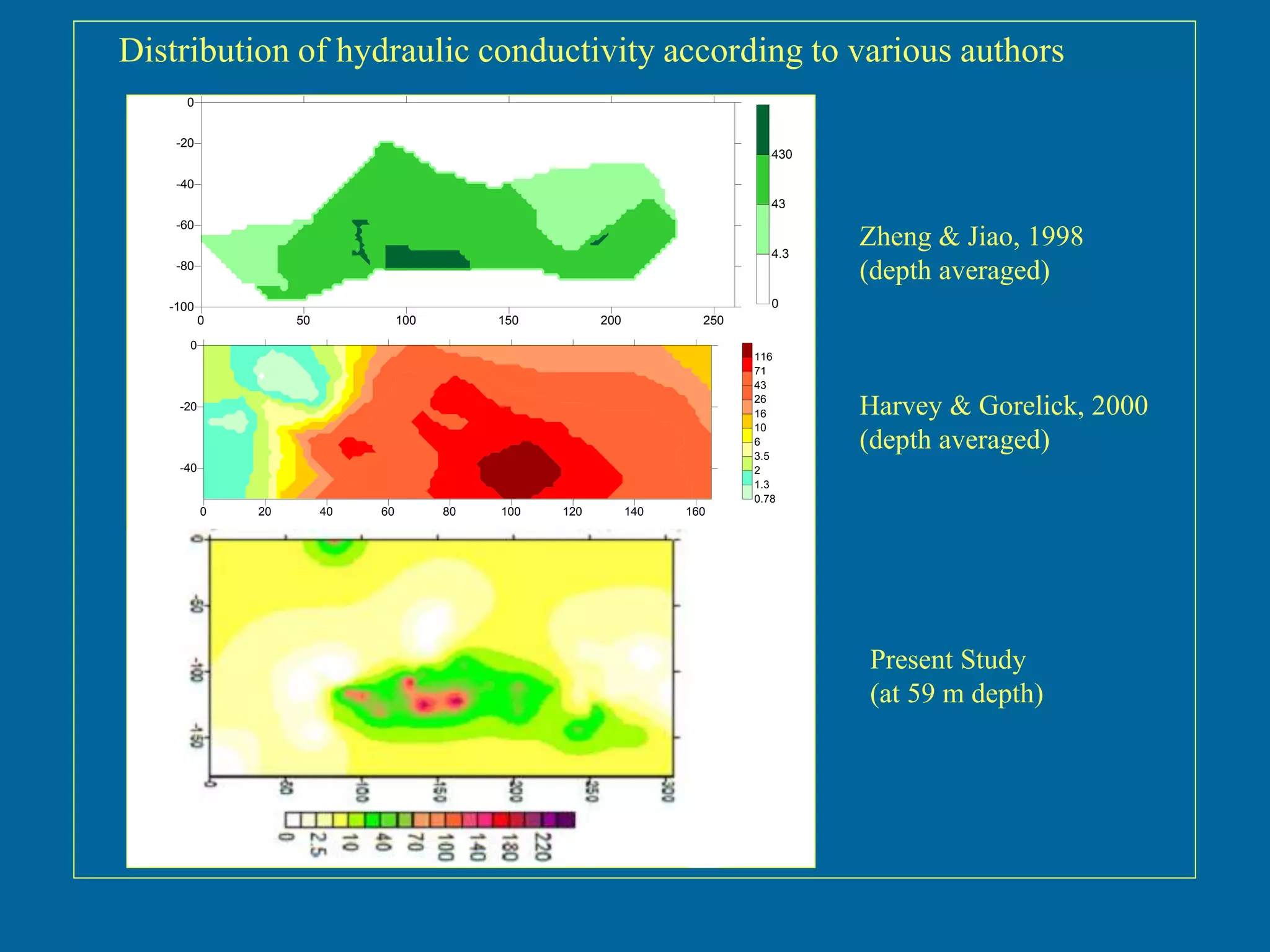
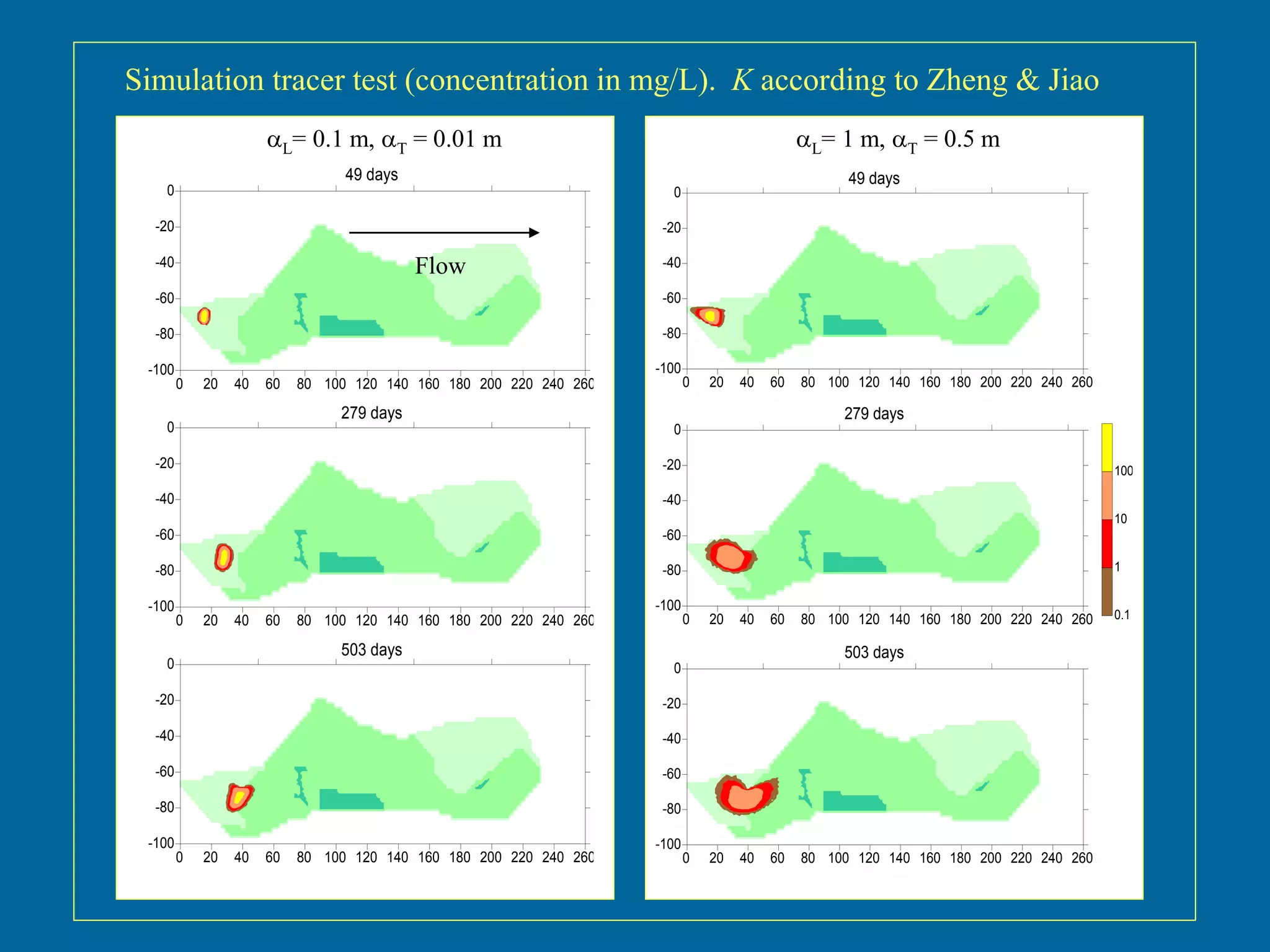
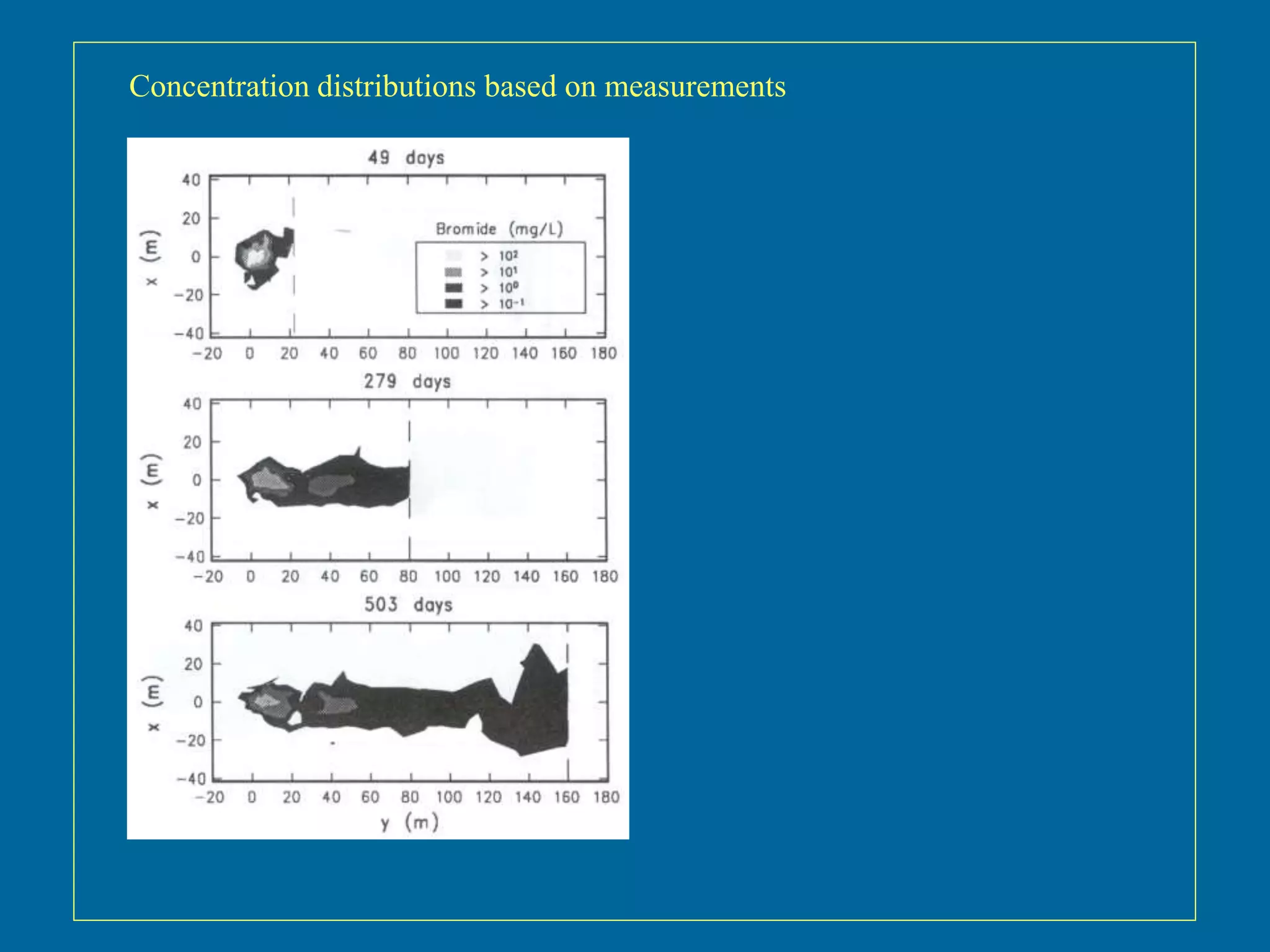
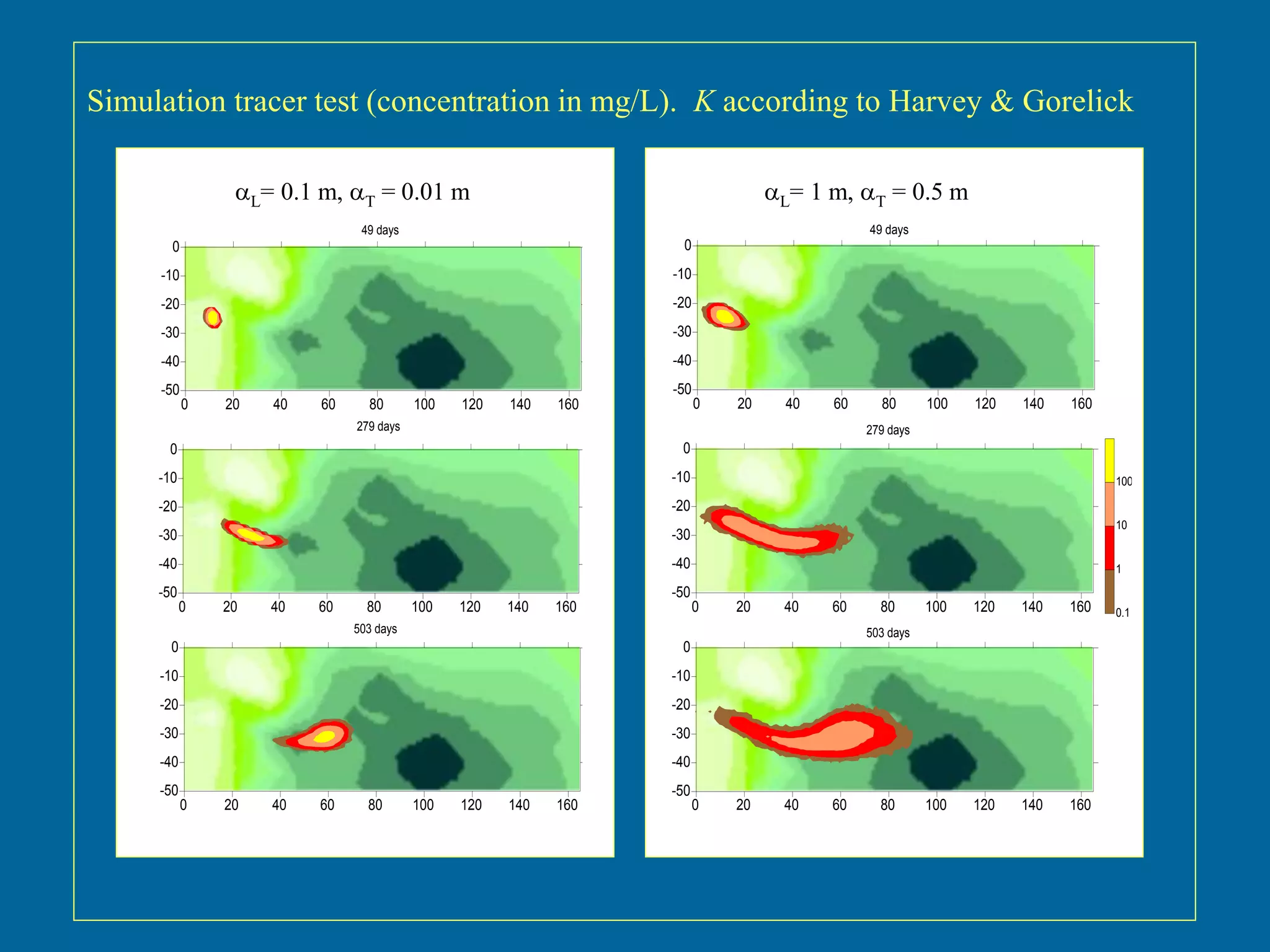
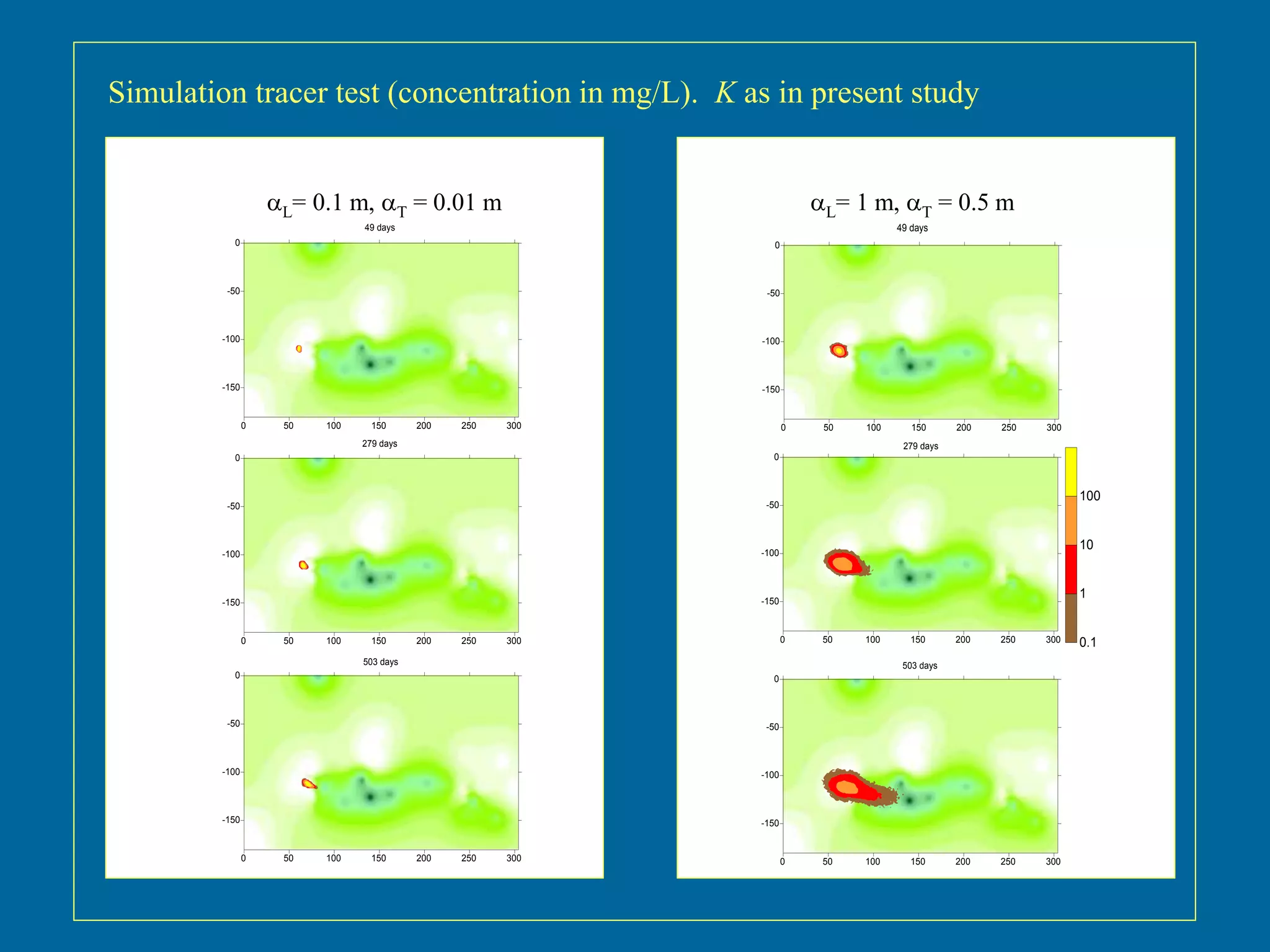
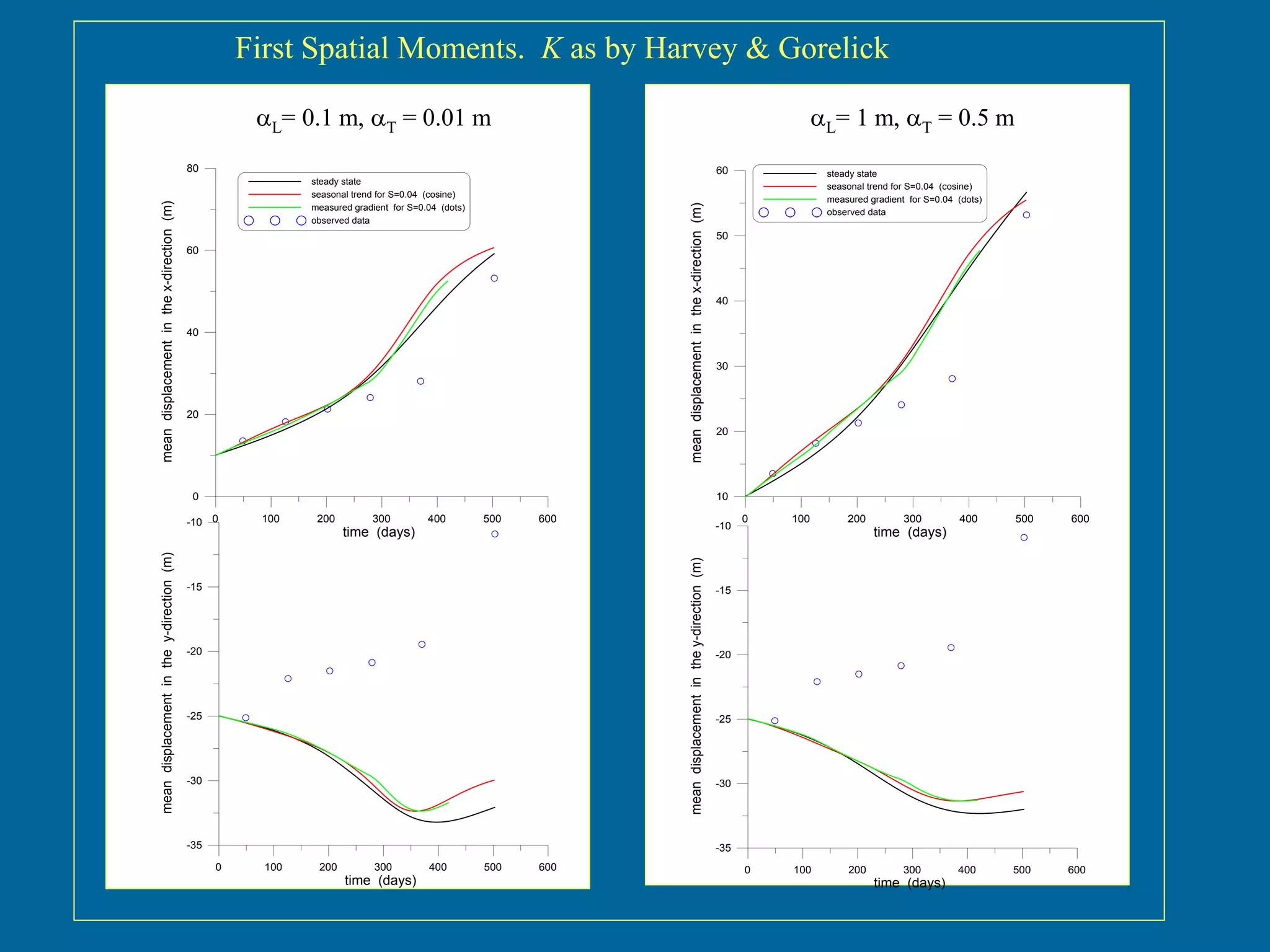
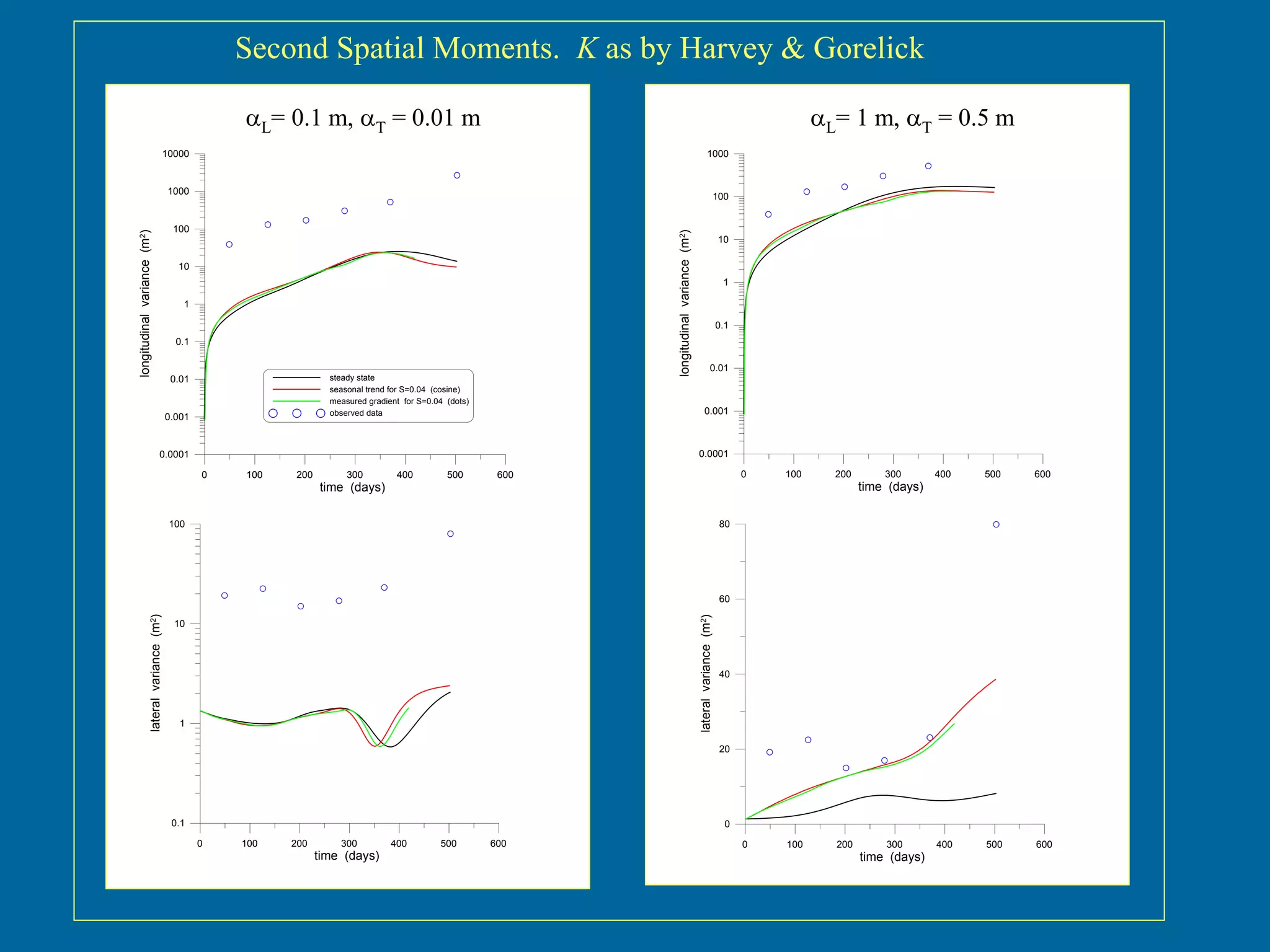
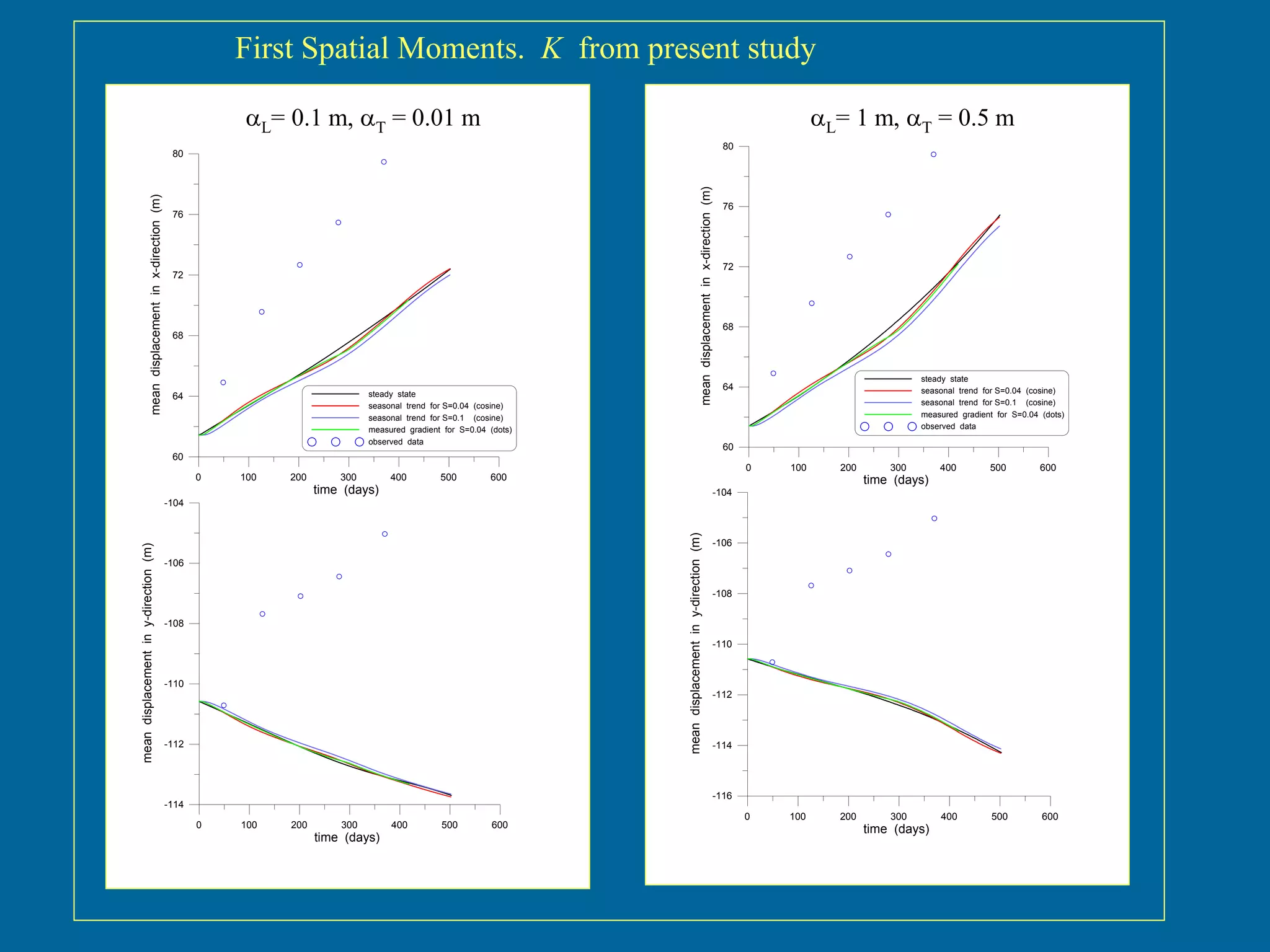
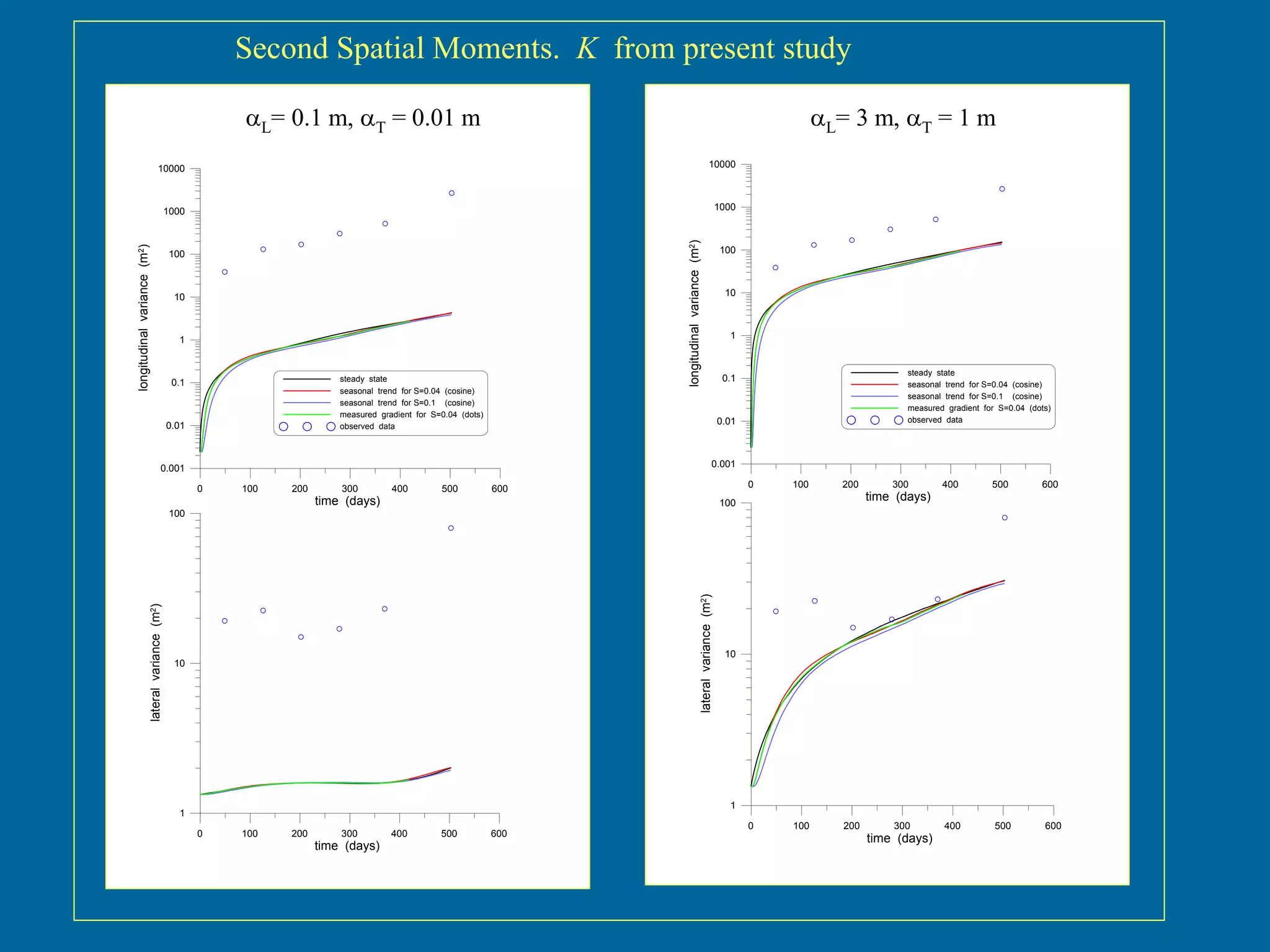
The document discusses simulations of tracer dispersion in a heterogeneous aquifer under steady and unsteady groundwater flow conditions. It highlights the impact of hydraulic conductivity on tracer distribution and the discrepancies observed between simulated and experimental data. The findings suggest that the flow type does not significantly affect tracer spreading, but accurate conductivity data is critical for realistic velocity fields.

1. Simulation of dispersion in a heterogeneous
aquifer: discussion of steady versus unsteady
groundwater flow
Gerard Uffink
Amro Elfeki
Sophie Lebreton
Delft University of Technology, Netherlands

2. Demo 1: Steady Flow
Demo 2: Unsteady Flow (fluctuations)
Transport in steady or unsteady groundwater flow

3. 0 400 800 1200 1600
time (days)
0
400
800
1200
1600
Longitudinal Variance
Steady flow
NonSteady flow
2
x
Increase of variance in time

4. MADE-1 site
Literature:
Boggs et al. 1992
Adams and Gelhar, 1992
Rehfeldt et al. 1992
Zheng and Jiao, 1998,
etc

5. Available:
- measurement of tracer distribution
- heads (contours) and fluctuations
- hydraulic conductivities (several options)
Not available
- dispersivities

6. Depth-averaged bromide concentration distributions
after 49, 279, and 503 days (Boggs et al., 1992).

7. Vertical position tracer plume

8. 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
time (months)
0.001
0.002
0.003
0.004
0.005
gradientmagnitude
measured gradient
fitted seasonal component
Head data
Fluctuations head gradient Contours of head

9. 0 50 100 150 200 250
-100
-80
-60
-40
-20
0
0
4.3
43
430
0 20 40 60 80 100 120 140 160
-40
-20
0
0.78
1.3
2
3.5
6
10
16
26
43
71
116
Zheng & Jiao, 1998
(depth averaged)
Harvey & Gorelick, 2000
(depth averaged)
Present Study
(at 59 m depth)
Distribution of hydraulic conductivity according to various authors

10. 0 20 40 60 80 100 120 140 160 180 200 220 240 260
-100
-80
-60
-40
-20
0
0 20 40 60 80 100 120 140 160 180 200 220 240 260
-100
-80
-60
-40
-20
0
0 20 40 60 80 100 120 140 160 180 200 220 240 260
-100
-80
-60
-40
-20
0
49 days
279 days
503 days
0 20 40 60 80 100 120 140 160 180 200 220 240 260
-100
-80
-60
-40
-20
0
0 20 40 60 80 100 120 140 160 180 200 220 240 260
-100
-80
-60
-40
-20
0
0 20 40 60 80 100 120 140 160 180 200 220 240 260
-100
-80
-60
-40
-20
0
0.1
1
10
100
49 days
279 days
503 days
Simulation tracer test (concentration in mg/L). K according to Zheng & Jiao
L= 1 m, T = 0.5 mL= 0.1 m, T = 0.01 m
Flow

11. Concentration distributions based on measurements

12. 0 20 40 60 80 100 120 140 160
-50
-40
-30
-20
-10
0
0 20 40 60 80 100 120 140 160
-50
-40
-30
-20
-10
0
0 20 40 60 80 100 120 140 160
-50
-40
-30
-20
-10
0
0.1
1
10
100
49 days
279 days
503 days
0 20 40 60 80 100 120 140 160
-50
-40
-30
-20
-10
0
0 20 40 60 80 100 120 140 160
-50
-40
-30
-20
-10
0
0 20 40 60 80 100 120 140 160
-50
-40
-30
-20
-10
0
49 days
279 days
503 days
L= 0.1 m, T = 0.01 m L= 1 m, T = 0.5 m
Simulation tracer test (concentration in mg/L). K according to Harvey & Gorelick

13. 49 days
279 days
503 days
0 50 100 150 200 250 300
-150
-100
-50
0
0 50 100 150 200 250 300
-150
-100
-50
0
0 50 100 150 200 250 300
-150
-100
-50
0
49 days
0 50 100 150 200 250 300
-150
-100
-50
0
0 50 100 150 200 250 300
-150
-100
-50
0
0 50 100 150 200 250 300
-150
-100
-50
0
279 days
503 days
0.1
1
10
100
L= 0.1 m, T = 0.01 m L= 1 m, T = 0.5 m
Simulation tracer test (concentration in mg/L). K as in present study

14. Comparison simulations and experiment
- head distribution good
- tracer distribution poor
Possible explanation
- hydraulic conductivity field uncertain
- velocity field uncertain
- ?? Steady versus unsteady flow ??

15. 0 100 200 300 400 500 600
time (days)
0
20
40
60
80meandisplacementinthex-direction(m)
steady state
seasonal trend for S=0.04 (cosine)
measured gradient for S=0.04 (dots)
observed data
0 100 200 300 400 500 600
time (days)
-35
-30
-25
-20
-15
-10
meandisplacementinthey-direction(m)
0 100 200 300 400 500 600
time (days)
10
20
30
40
50
60
meandisplacementinthex-direction(m)
steady state
seasonal trend for S=0.04 (cosine)
measured gradient for S=0.04 (dots)
observed data
0 100 200 300 400 500 600
time (days)
-35
-30
-25
-20
-15
-10
meandisplacementinthey-direction(m)
L= 0.1 m, T = 0.01 m
First Spatial Moments. K as by Harvey & Gorelick
L= 1 m, T = 0.5 m

16. L= 0.1 m, T = 0.01 m
Second Spatial Moments. K as by Harvey & Gorelick
L= 1 m, T = 0.5 m
0 100 200 300 400 500 600
time (days)
0.0001
0.001
0.01
0.1
1
10
100
1000
10000
longitudinalvariance(m2)
steady state
seasonal trend for S=0.04 (cosine)
measured gradient for S=0.04 (dots)
observed data
0 100 200 300 400 500 600
time (days)
0.1
1
10
100
lateralvariance(m2)
0 100 200 300 400 500 600
time (days)
0.0001
0.001
0.01
0.1
1
10
100
1000
longitudinalvariance(m2)
0 100 200 300 400 500 600
time (days)
0
20
40
60
80
lateralvariance(m2)

17. L= 0.1 m, T = 0.01 m
First Spatial Moments. K from present study
L= 1 m, T = 0.5 m
0 100 200 300 400 500 600
time (days)
60
64
68
72
76
80meandisplacementinx-direction(m)
steady state
seasonal trend for S=0.04 (cosine)
seasonal trend for S=0.1 (cosine)
measured gradient for S=0.04 (dots)
observed data
0 100 200 300 400 500 600
time (days)
-114
-112
-110
-108
-106
-104
meandisplacementiny-direction(m)
0 100 200 300 400 500 600
time (days)
60
64
68
72
76
80
meandisplacementinx-direction(m)
steady state
seasonal trend for S=0.04 (cosine)
seasonal trend for S=0.1 (cosine)
measured gradient for S=0.04 (dots)
observed data
0 100 200 300 400 500 600
time (days)
-116
-114
-112
-110
-108
-106
-104
meandisplacementiny-direction(m)

18. L= 0.1 m, T = 0.01 m
Second Spatial Moments. K from present study
L= 3 m, T = 1 m
0 100 200 300 400 500 600
time (days)
0.001
0.01
0.1
1
10
100
1000
10000
longitudinalvariance(m2)
steady state
seasonal trend for S=0.04 (cosine)
seasonal trend for S=0.1 (cosine)
measured gradient for S=0.04 (dots)
observed data
0 100 200 300 400 500 600
time (days)
1
10
100
lateralvariance(m2)
0 100 200 300 400 500 600
time (days)
0.001
0.01
0.1
1
10
100
1000
10000
longitudinalvariance(m2)
steady state
seasonal trend for S=0.04 (cosine)
seasonal trend for S=0.1 (cosine)
measured gradient for S=0.04 (dots)
observed data
0 100 200 300 400 500 600
time (days)
1
10
100
lateralvariance(m2)

19. Concluding remarks
- steady or unstead flow seems to have
no effect on spreading of tracer
- good conductivity field is essential to
reproduce realistic velocity field
- 2D versus 3D ??