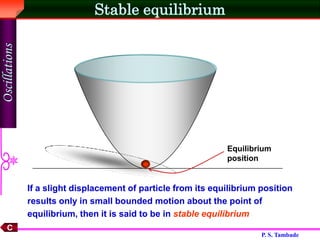
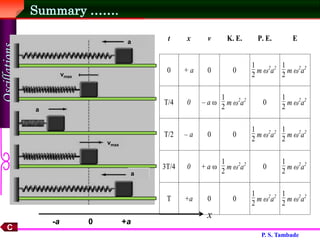
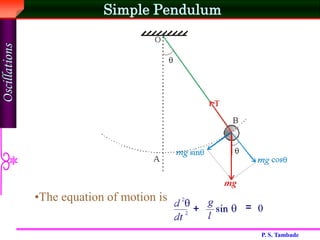
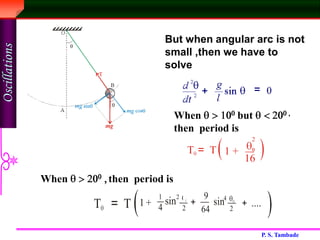
Simple harmonic motion (SHM) is oscillatory motion where the restoring force is directly proportional to the displacement. SHM includes the motion of a spring-mass system and a simple pendulum with small oscillations. The displacement of SHM follows the equation x = a sin(ωt + φ), where a is the amplitude, ω is the angular frequency, t is time, and φ is the phase. The period and frequency depend only on the spring constant or mass and gravitational field. Energy oscillates between potential and kinetic forms with the total mechanical energy conserved.

1. SIMPLE HARMONIC MOTION
Dr. Popat S. Tambade
Associate Professor
Prof. Ramkrishna More Arts, Commerce and Science College
Akurdi, Pune 411 044

2. Content
1. Equilibrium
2. Stable equilibrium
Oscillations
3. Unstable Equilibrium
4. Oscillatory Motion
5. Spring –Mass system
6. Simple harmonic Motion
7. Displacement and velocity
8. Periodic Time
9. Frequency
10.Displacement and Acceleration
 11.Energy of SHM
12.Lissajous Figures
13.Angular SHM
14.Simple Pendulum
P. S. Tambade

3. Equilibrium
The body is said to be in equilibrium at a point
Oscillations
when net force acting on the body at that point is
zero.
• Types of equilibriums
1. Stable Equilibrium
2. Unstable equilibrium
 3. Neutral equilibrium
C
P. S. Tambade

4. Oscillations Stable equilibrium
Equilibrium
 position
If a slight displacement of particle from its equilibrium position
results only in small bounded motion about the point of
equilibrium, then it is said to be in stable equilibrium
C
P. S. Tambade

5. Potential energy curve for stable equilibrium
Tangent at B V(x) Tangent at A
Oscillations
B A
dV dV
Slope = Slope =
dx dx
Negative Positive
F F
 -a 0 +a
x
-x x
Force
dV
F = Force is positive i.e. directed towards equilibrium
negative i.e. directed towards equilibrium
dx position
Simulation
C
P. S. Tambade

6. Unstable equilibrium
Equilibrium
Oscillations
position

If a slight displacement of the particle from its equilibrium position
results unbounded motion away from the equilibrium
position, then it is said to be in unstable equilibrium
C
P. S. Tambade

7. Potential energy curve for unstable equilibrium
V(x) Tangent at A
Oscillations
dV B A dV
Slope = Slope =
dx dx
Positive Negative
Tangent at B
F F
x
 -a -x
0
x +a
Force
dV
F = Force is negative i.e. directed away from equilibrium
Force is positive i.e. directed away from equilibrium
dx
position
position
C
P. S. Tambade

8. Oscillatory Motion
Any motion that repeats itself after equal intervals of time is called
periodic motion.
Oscillations
If an object in periodic motion moves back and forth over the
same path, the motion is called oscillatory or vibratory motion

C
P. S. Tambade

9. Oscillations Spring-Mass system
m Relaxed mode
x=0
F
m
Extended mode
x
 m
F
Compressed mode
–x
We know that for an ideal
spring, the force is related
to the displacement by
F kx
C
P. S. Tambade

10. Simple Harmonic Motion
Linear simple harmonic motion :
When the force acting on the particle is directly
Oscillations
proportional to the displacement and opposite in
direction, the motion is said to be linear simple harmonic
motion
F kx
Differential equation of motion is
d 2x
m 2 + kx = 0 where
2
dt k m
d 2x k
2 + ω x=0
2
dt m
 Solution is
x = a sin (ωt + )
(ωt + ) is called phase and is called epoch of SHM
C
P. S. Tambade

11. The displacement of particle from equilibrium position is
Oscillations
x = a sin (ωt + )
• a and are determined uniquely by the position
and velocity of the particle at t = 0
• If at t = 0 the particle is at x = 0, then =0
• If at t = 0 the particle is at x = a, then = π/2
• The phase of the motion is the quantity (ωt + )
• x (t) is periodic and its value is the same each
time ωt increases by 2π radians
C
P. S. Tambade

12. Oscillations
Simple harmonic motion (or SHM) is the
sinusoidal motion executed by a particle of
mass m subject to one-dimensional net
force that is proportional to the
displacement of the particle from
equilibrium but opposite in sign

C
P. S. Tambade

13. Equation of SHM is
Oscillations
x = a sin (ωt + )
The velocity is
dx
v = dt
v = aω cos (ωt + )
 or v = ω a2 x2
The velocity is zero at extreme positions and maximum
at equilibrium position
C
P. S. Tambade

14. Graphs of Displacement and Velocity
x = a sin (ωt + ) v = aω cos (ωt + )
Oscillations
π
For =
2
π
x ωT
T
2
+a
v
π π 3π 2π 5π 3π 7π 4π t, time
 2 2 2 2 ω
T T
ωt
-a
π
2
T is = 2 , difference between velocity and displacement is π
ωT called periodic time
The phase The period of oscillation is T = 2 / ω
2
C
P. S. Tambade

15. Periodic Time
The period of SHM is defined as the time taken by the
Oscillations
oscillator to perform one complete oscillation
After every time T, the particle will have the same
position, velocity and the direction
2 m
T T 2
k
T
 T m whe nk is constant
1
T whe nm is constant
k
m
C
P. S. Tambade

16. Frequency
The frequency represents the number of
oscillations that the particle undergoes per
Oscillations
unit time interval
• The inverse of the period is called the
frequency
1
ƒ
T 2
1 k
 f
2 m
•Units are cycles per second = hertz (Hz)
C
P. S. Tambade

17. m 1 k
T 2
Oscillations
f
k 2 m
• The frequency and the period depend only on the mass of
the particle and the force constant of the spring
• They do not depend on the parameters of motion like
amplitude of oscillation
• The frequency is larger for a stiffer spring (large values of k)
 and decreases with increasing mass of the particle
C
P. S. Tambade

18. Displacement and acceleration
x = a sin (ωt + ) A = - aω2 sin (ωt + )
Oscillations
π
For =
2
x π
π 5π
ωt
π 3π 2π 3π 7π 4π
2 2 2 2
 Ax
π
The phase difference between acceleration and displacement is π
C
P. S. Tambade

19. Energy
The potential energy is
Oscillations
1
V= 2
k x2
The kinetic energy is
1
K= 2
mv2
1
or K= 2
m ω 2 (a2 – x2)
The total energy is
 E=K + V
1
or E= 2
m ω 2 a2
Thus, total energy of the oscillator is constant and proportional to
the square of amplitude of oscillations
C
P. S. Tambade

20. Summary …….
a
t x v K. E. P. E. E
Oscillations
1 2 2 1
0 +a 0 0 mωa m ω2a2
vmax 2 2
1 1
T/4 0 –aω m ω2a2 0 m ω2a2
a 2 2
1 1
T/2 –a 0 0 m ω2a2 m ω2a2
vmax
2 2
 3T/4 0 +aω
1
m ω2a2 0
1
m ω2a2
A
a max 2 2
1 1
T +a 0 0 m ω2a2 m ω2a2
2 2
x
-a 0 +a
C
P. S. Tambade

21. Graphical Representation of K. E. and P. E.
Energy
1
Oscillations
E= 2
m ω 2 a2
P. E.
P. E. = K. E.
 K. E.
x
-a 0 a/ 2 +a
- a/ 2
The total mechanical energy is constant
The total mechanical energy is proportional to the square of the amplitude
Energy is continuously being transferred between potential energy stored
C in the spring and the kinetic energy of the block
P. S. Tambade

22. Variation of K.E. and P. E. With time
1 1
x = a sin (ωt + ) V= 2
k x2 K= 2
m ω 2 (a2 – x2)
x
Oscillations
0
π π 3π 5π 3π 7π
ωt
2π 4π
2 2 2 2
π
For = 2
E
K. E.

P. E.
0 ωt
For one cycle of oscillation of particle there are two cycles for K. E.
and P.E.. Thus frequency of K. E. or P. E. is 2
C
P. S. Tambade

23. Angular SHM
If path of particle of a body performing an oscillatory
motion is curved, the motion is known as angular
Oscillations
simple harmonic motion
Definition : Angular simple harmonic motion is defined
as the oscillatory motion of a body in which the body is
acted upon by a restoring torque (couple) which is
directly proportional to its angular displacement from
the equilibrium position and directed opposite to the
angular displacement
P. S. Tambade

24. Angular SHM ……
The restoring torque is
Oscillations
is the torsion constant of the support wire
Newton’s Second Law gives
d2 I – moment of inertia
I 2
dt
 d2 d2
I 2 0
dt dt 2 I
d2 2
0 0 sin ( t )
dt 2
P. S. Tambade

25. • The torque equation produces a motion equation
for simple harmonic motion
Oscillations
• The angular frequency is
I
I
• The period is T 2
– No small-angle restriction is necessary
– Assumes the elastic limit of the wire is not exceeded

C
P. S. Tambade

26. Oscillations Simple Pendulum

•The equation of motion is
P. S. Tambade

27. Oscillations
• When angle is very small, we have sin
 d
2
g
2 +
= 0
dt l
The Period is l
T=2
g
P. S. Tambade

28. But when angular arc is not
Oscillations
small ,then we have to
solve
When but
then period is
2
T = T 1+
 16
When then period is
1 9
T = T 1+ 4 sin2 + sin4 + ....
2 64 2
P. S. Tambade

29. Oscillations

Dr. P. S. Tambade received an outstanding paper award in E-Learn
2008, Las Vegas
P. S. Tambade