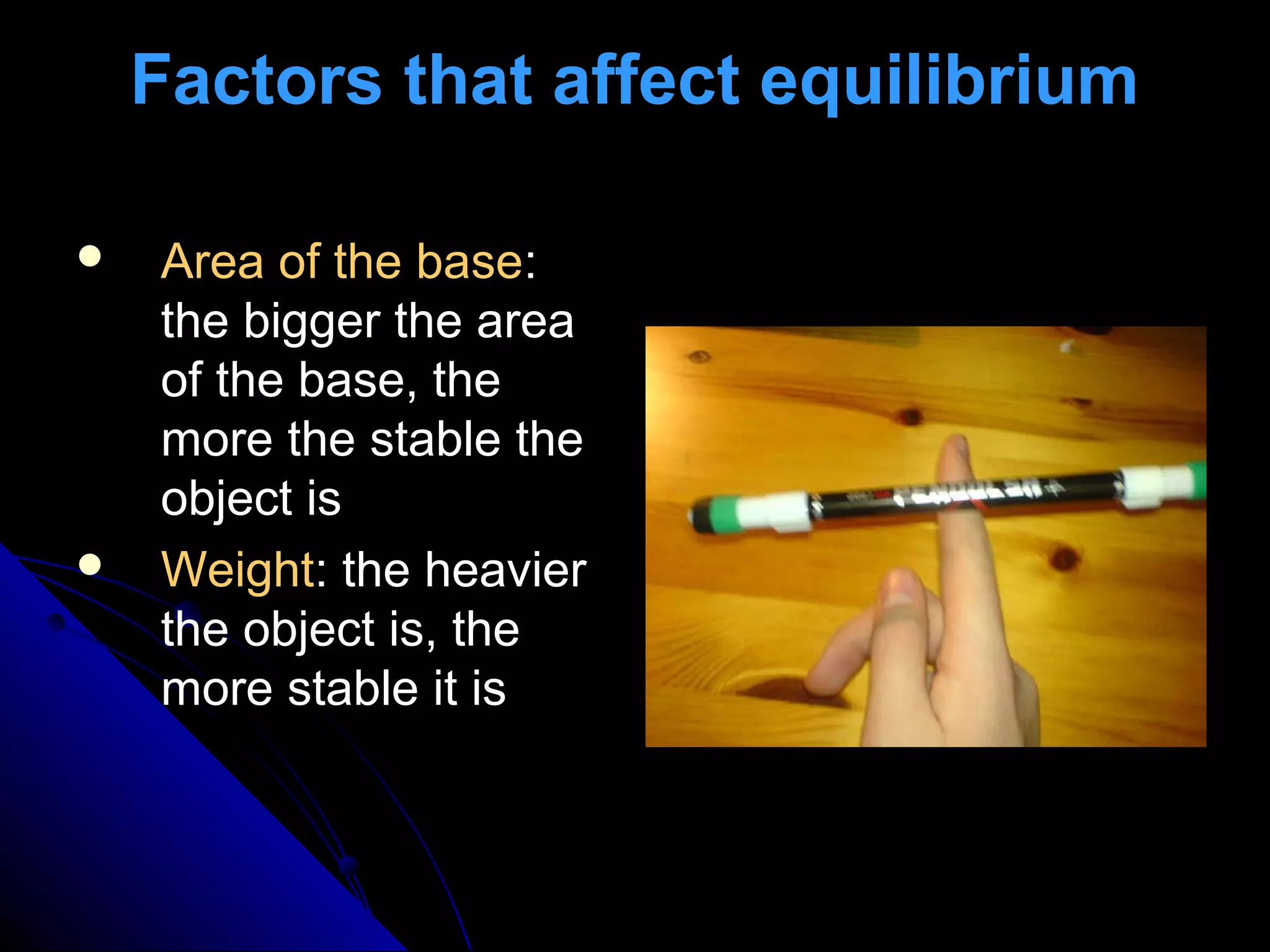
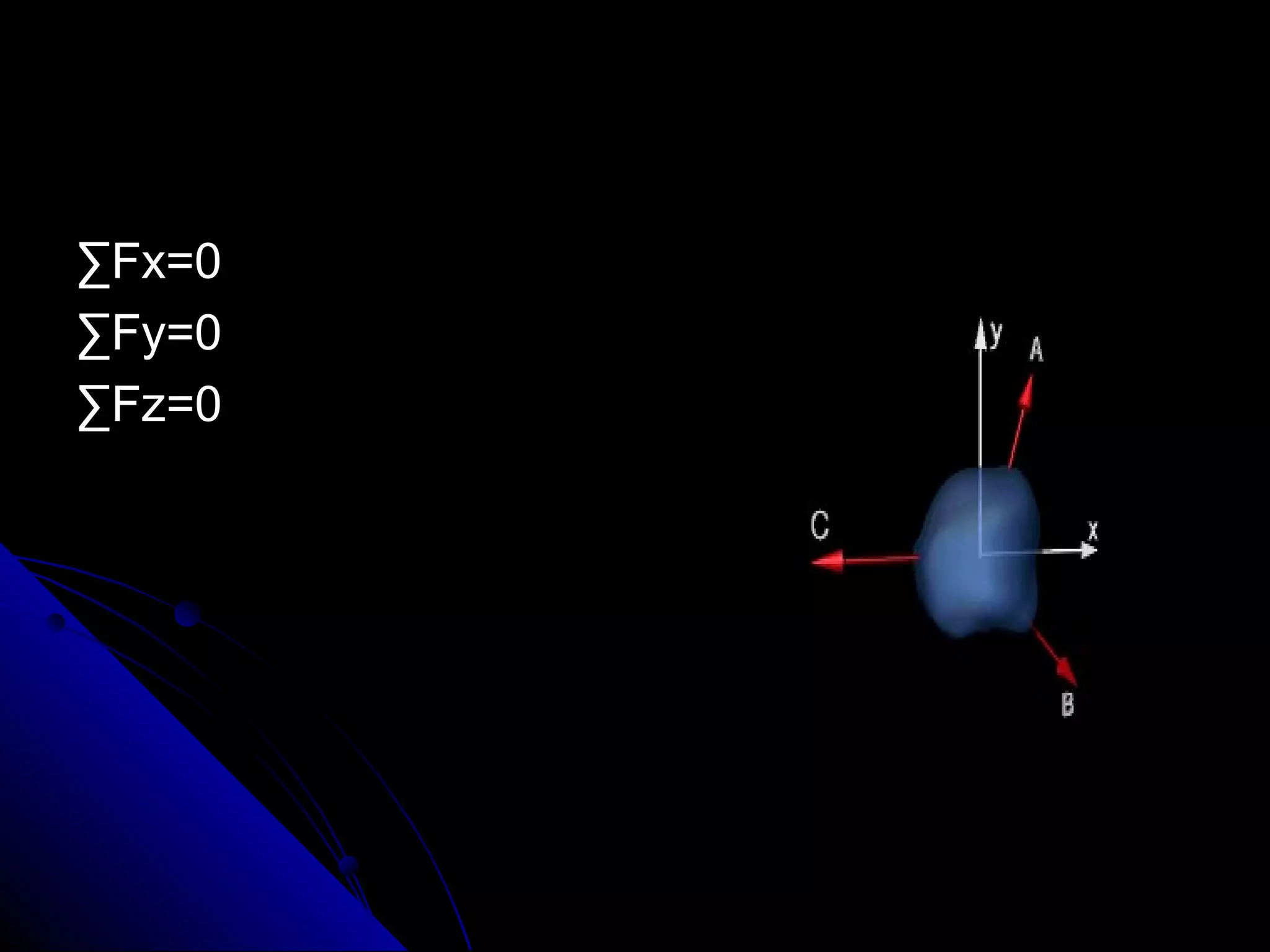
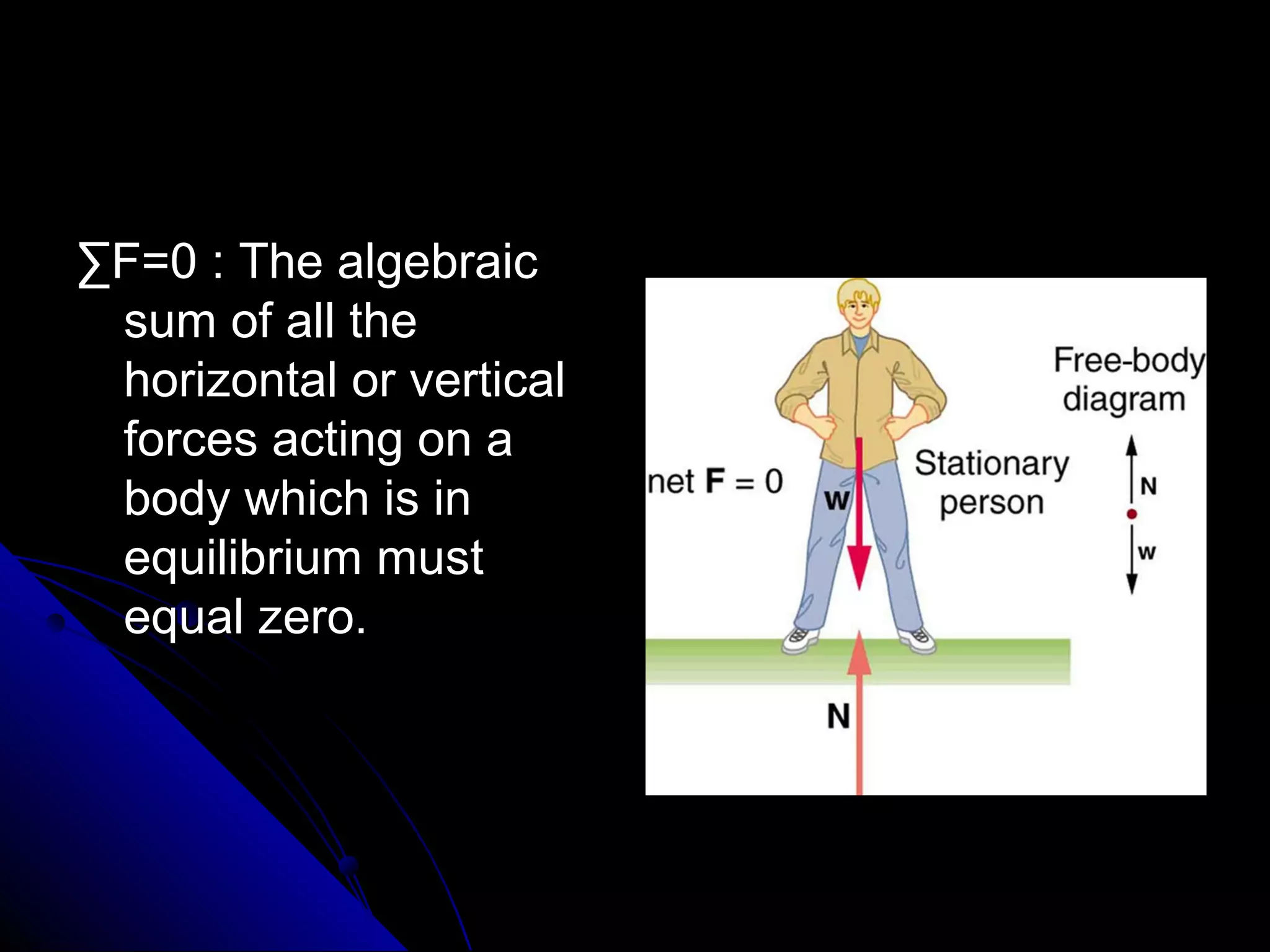
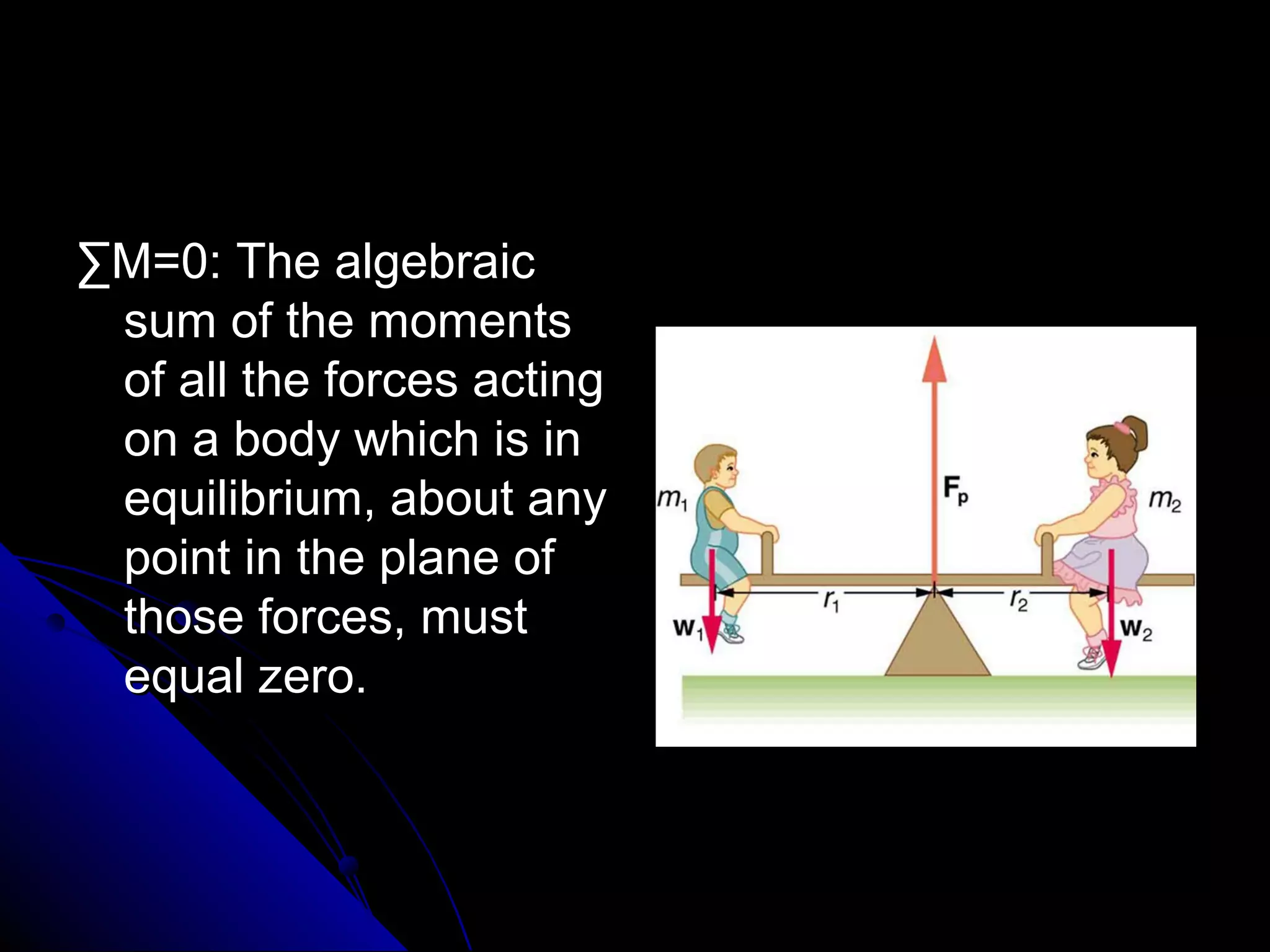
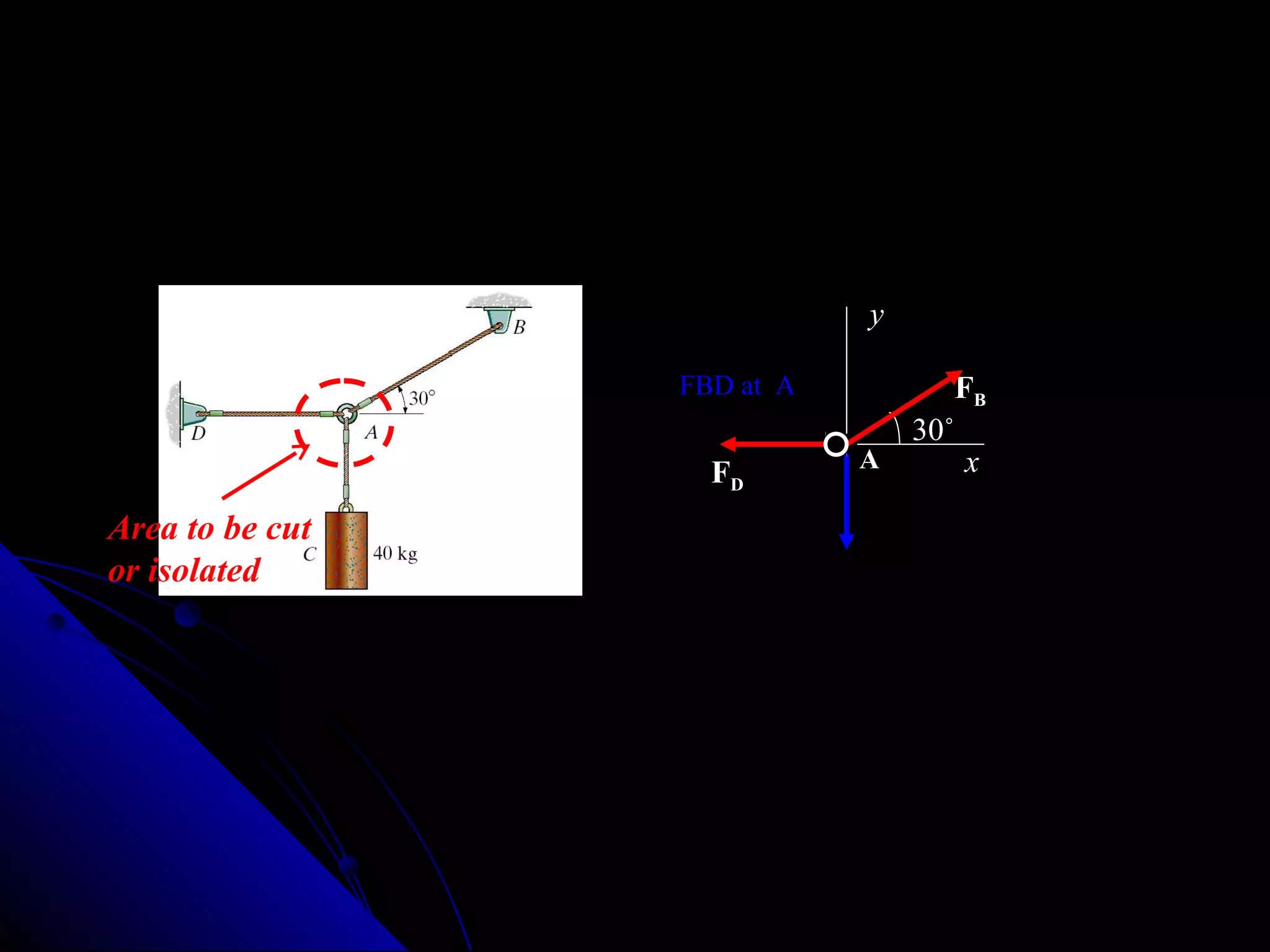
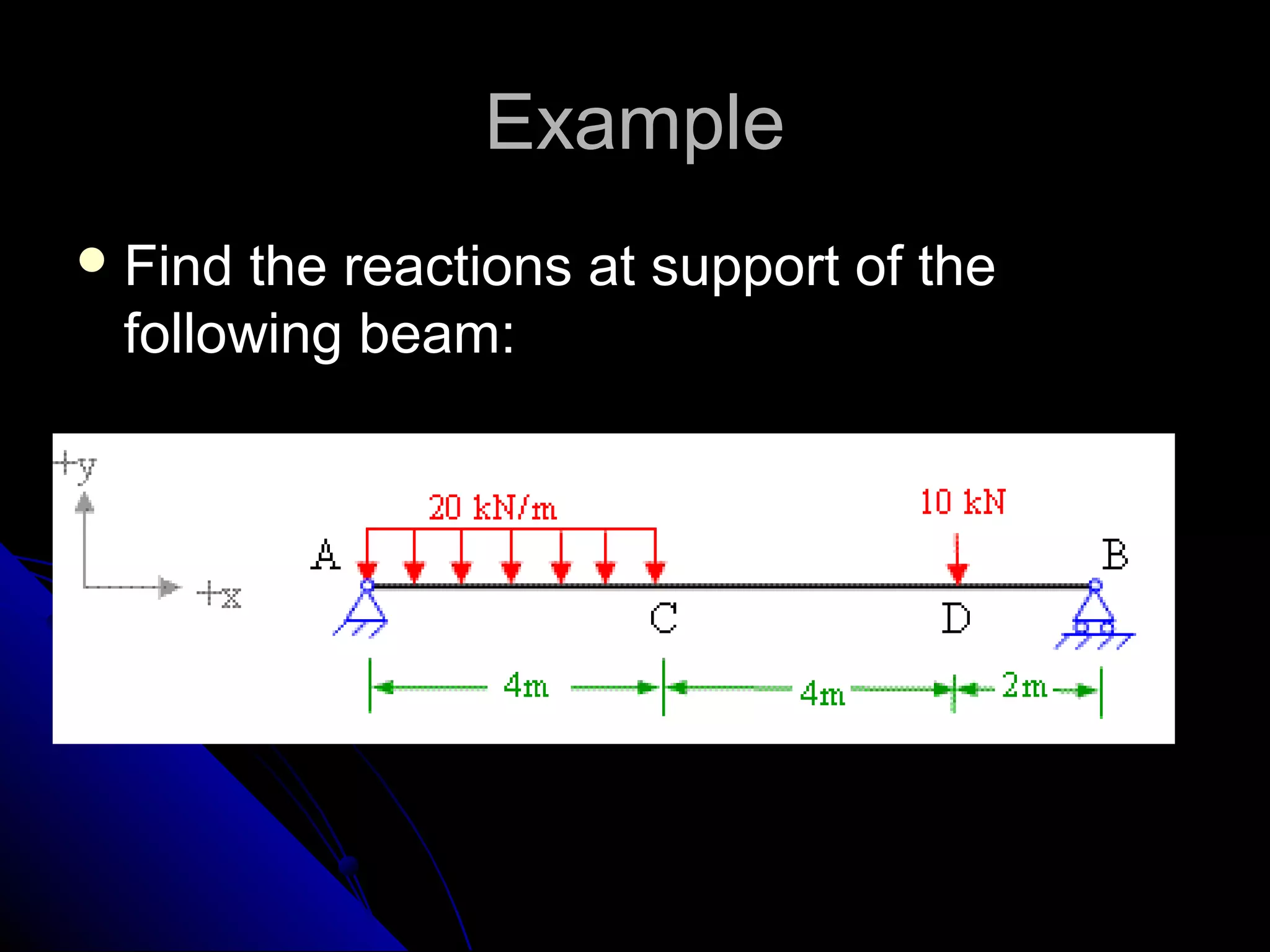
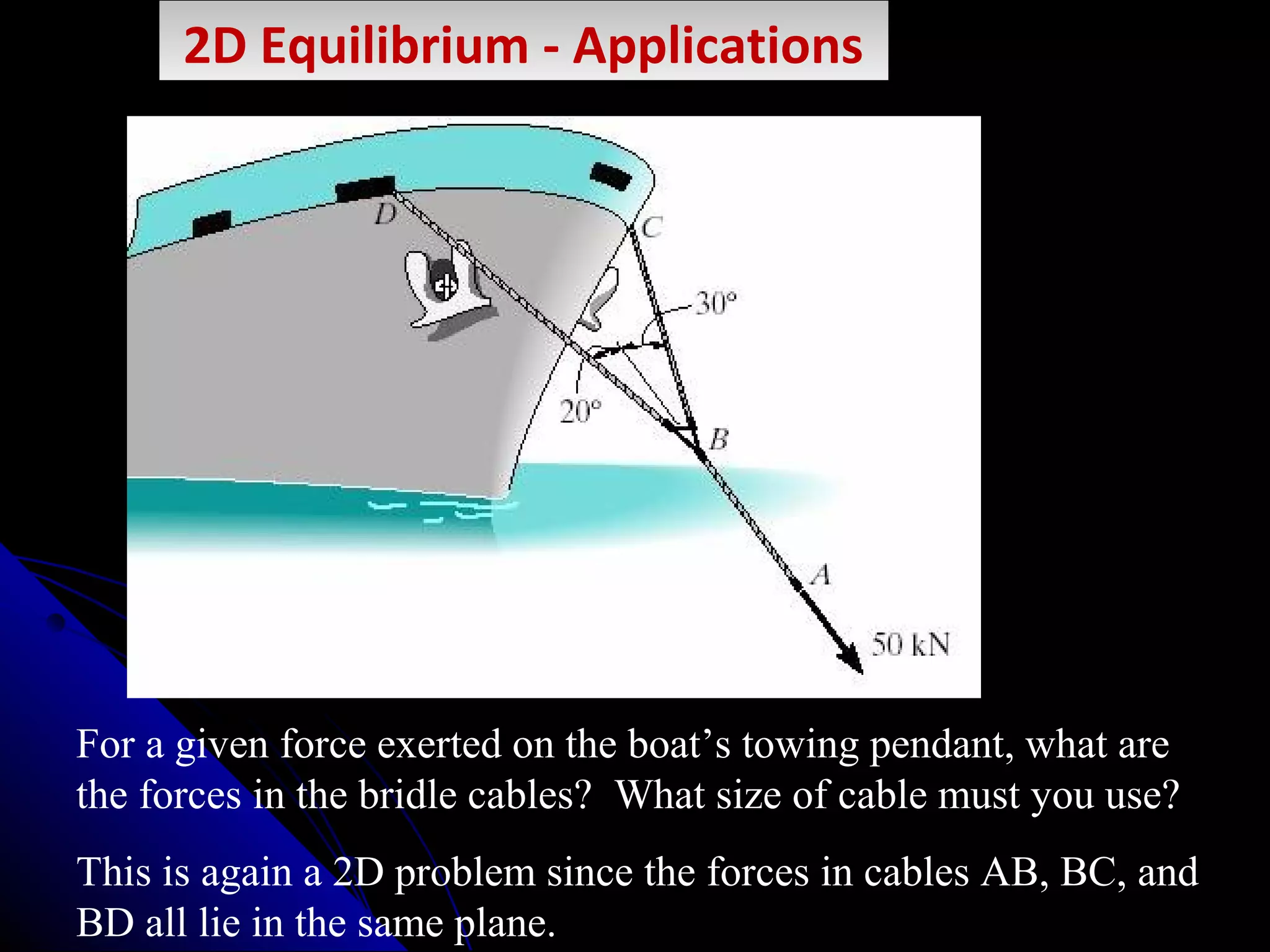
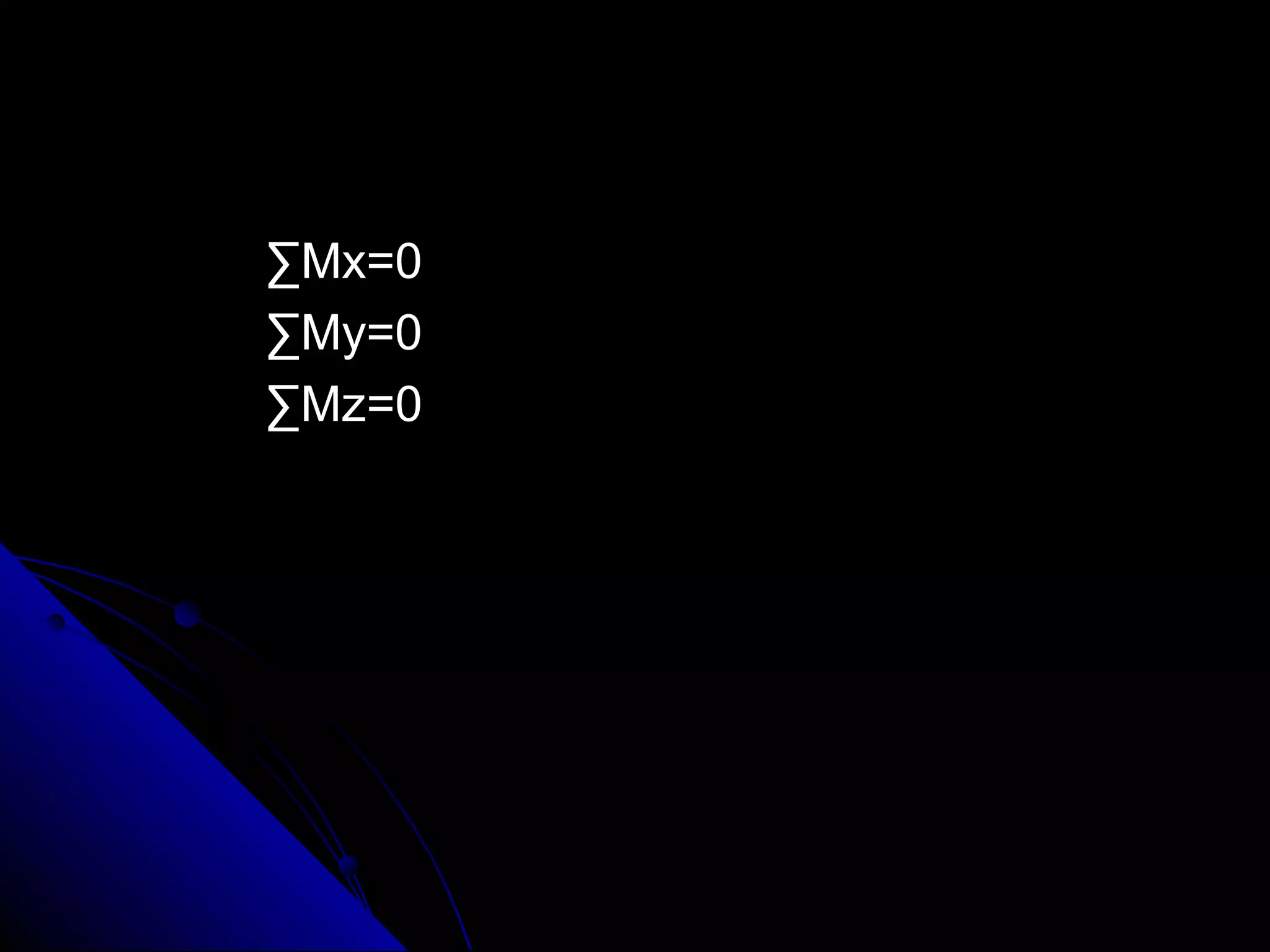This presentation discusses the concept of equilibrium in 2 dimensions. Equilibrium occurs when the net force and net torque on an object are both zero. This allows the object to remain at rest or in uniform motion. The key equations of equilibrium in 2D are: the sum of the horizontal forces equals 0 (ΣFx=0), the sum of the vertical forces equals 0 (ΣFy=0), and the sum of torques about the z-axis equals 0 (ΣMz=0). Examples are provided to demonstrate how to apply these equations to solve for unknown forces by drawing a free body diagram and setting up the appropriate equilibrium equations.

1. WELCOME TO MY
PRESENTATION

2. AHSANULLAH UNIVERSITY
OF
SCIENCE AND TECHNOLOGY
PRE-STRESSED CONCRETE
SESSIONAL

3. PRESENTED BY
MUNSHI MD. RASEL
ID: 10.01.03.075
SECTION B
4th YEAR AND 2nd SEMESTER
DEPARTMENT OF CIVIL ENGINEERING

4. PRESENTATION TOPIC
EQUILIBRIUM AND EQUATION OF
EQUILIBRIUM:2D

5. Equilibrium
A body is said to be in
equilibrium if it is at
rest or moving with
uniform velocity.

6. Newton’s First Law of Motion: If the
resultant force on a particle is zero, the
particle will remain at rest or will
continue at constant speed in a straight
line.

7. Factors that affect equilibrium


Area of the base:
the bigger the area
of the base, the
more the stable the
object is
Weight: the heavier
the object is, the
more stable it is

8. Types of Equilibrium
 Static
Equilibrium
 Dynamic Equilibrium

9. Static Equilibrium
If some forces are
acting on a body
horizontally or
vertically, and the
body remains it states
of rest is called Static
Equilibrium. Example:
A book lying on a
table.

10. Dynamic Equilibrium
If some forces are
acting on a body
horizontally or
vertically, and the
body remains it states
of motion is called
Dynamic Equilibrium.
Example: A train is
moving with uniform
velocity.

11. Equations of equilibrium
Consider an object
moving along the xaxis. If no net force is
applied to the object
along the x-axis, it will
continue to move
along the x-axis at a
constant velocity with
no acceleration. We
can extend this to the
y- and z- axes.

12. In static systems, where motion does not
occur, the sum of the forces in all
directions must always equal zero
(otherwise, it's a dynamics problem). This
concept can be represented
mathematically with the following
equations:

13. ∑Fx=0
∑Fy=0
∑Fz=0

14.  The
concept also applies to rotational
motion.
 If the resultant moment about an axis is
zero, the object will have no rotational
acceleration about the axis. Again, we can
extend this to moments about the y-axis
and the z-axis. This is represented
mathematically with the following.

15. ∑Mx=0
∑My=0
∑Mz=0

16. ∑F=0 : The algebraic
sum of all the
horizontal or vertical
forces acting on a
body which is in
equilibrium must
equal zero.

17. ∑M=0: The algebraic
sum of the moments
of all the forces acting
on a body which is in
equilibrium, about any
point in the plane of
those forces, must
equal zero.

18. There are six equations expressing the
equilibrium of a rigid body in 3 dimensions.
∑Fx=0
∑Fy=0
∑Fz=0
∑Mx=0
∑My=0 ∑Mz=0

19. In two dimensions one direction of force
and two directions of moments can be
ignored. When forces exist only in the x
and y directions, there cannot be a
moment in any direction except z. The
equations of concern when forces only
exist in the x and y directions are shown
below:

20. ∑Fx=0
∑Fy=0
∑Mz=0

21. How to apply equations of
equilibrium?
 First
draw a free body diagram of the
structure or its member.
 If a member is selected, it must be
isolated from its supports and
surroundings.
 All the forces and couple moments must
be shown acting on the member.
 Then apply the equations of equilibrium.

22. y
FBD at A
FD A
Area to be cut
or isolated
FB
A
30˚
x

23. Example
 Find
the reactions at support of the
following beam:

24. Applying eqn of equilibrium:
∑Fx=0;
Ax=0
∑Fy=0;
Ay+By-10-20*4=0
Ay+By=90kn………(1)

25. Considering Z axis passing through A and
taking moment of all the forces about Zaxis (taking clockwise –ve and
anticlockwise +ve)
∑Mz=0; By*10-10*8-20*4*2=0
By=24kn
Putting this value in eqn (1) we get,
Ay=66kn.

26. 2D Equilibrium - Applications
Since the forces involved in supporting the spool lie in a plane, this is
essentially a 2D equilibrium problem. How would you find the forces in
cables AB and AC?

27. 2D Equilibrium -- Applications
2D Equilibrium Applications
For a given force exerted on the boat’s towing pendant, what are
the forces in the bridle cables? What size of cable must you use?
This is again a 2D problem since the forces in cables AB, BC, and
BD all lie in the same plane.

28. Summary
•
In order for an object to be in equilibrium,
there must be no net force on it along any
coordinate, and there must be no net
torque around any axis.
•
2D equations of equilibrium:
∑Fx=0
∑Fy=0
∑Mz=0

29. Thanks for your kind attention
Any Questions?