The document discusses dependent pair types (Σ-types), which allow the type of the second element of a pair to depend on the value of the first. It provides the formation rules, introduction and elimination rules, computation rules, and uniqueness principle for Σ-types. Examples of Σ-types are implemented in Idris and Scala using dependent functions and implicits.

1. Dependent pair type (Σ-type)
Dmytro Mitin
https://stepik.org/course/Introduction-to-programming-
with-dependent-types-in-Scala-2294/
March 2017
Dmytro Mitin Dependent pair type (Σ-type)

2. Sets
Union of set family
α∈A
Bα = b ∃α ∈ A b ∈ Bα
Disjoint union of set family
α∈A
Bα = (α, b) α ∈ A , b ∈ Bα
Dmytro Mitin Dependent pair type (Σ-type)

3. Dependent pair type (Σ-type)
1 Type Formation
Γ A : ∗ Γ, x : A B : ∗
Γ
x:A
B : ∗
2 Constructor
Γ a : A Γ, x : A B : ∗ Γ b : B[x ← a]
Γ (a, b) :
x:A
B
3 Eliminators
Γ p :
x:A
B
Γ fst p : A
Γ p :
x:A
B
Γ snd p : B[x ← fst p]
Dmytro Mitin Dependent pair type (Σ-type)

4. Dependent pair type (Σ-type)
4 Computation rules (”β-reduction“)
Γ a : A Γ, x : A B : ∗ Γ b : B[x ← a]
Γ fst(a, b) ≡ a : A
Γ a : A Γ, x : A B : ∗ Γ b : B[x ← a]
Γ snd(a, b) ≡ b : B
5 Uniqueness principle (”η-conversion“)
Γ p :
x:A
B
Γ (fst p, snd p) ≡ p :
x:A
B
Dmytro Mitin Dependent pair type (Σ-type)

5. Partial case
Partial case of
x:A
B
is sum type (coproduct)
B1 + B2
Dmytro Mitin Dependent pair type (Σ-type)

6. Idris
data DepPair : (a : Type) -> (P : a -> Type) -> Type where
MakeDepPair : {P : a -> Type} -> (x : a) -> P x -> DepPair a P
depType : Int -> Type
depType 0 = Int
depType 1 = String
depType = Bool
x : DepPair Int (n => depType n)
x = MakeDepPair 1 "a"
x1 : DepPair Int (n => depType n)
x1 = MakeDepPair 0 10
x2 : DepPair Int (n => depType n)
x2 = MakeDepPair 2 True
Dmytro Mitin Dependent pair type (Σ-type)

7. Idris
x3 : DepPair Int (n => depType n)
x3 = MakeDepPair 0 "a"
Dmytro Mitin Dependent pair type (Σ-type)

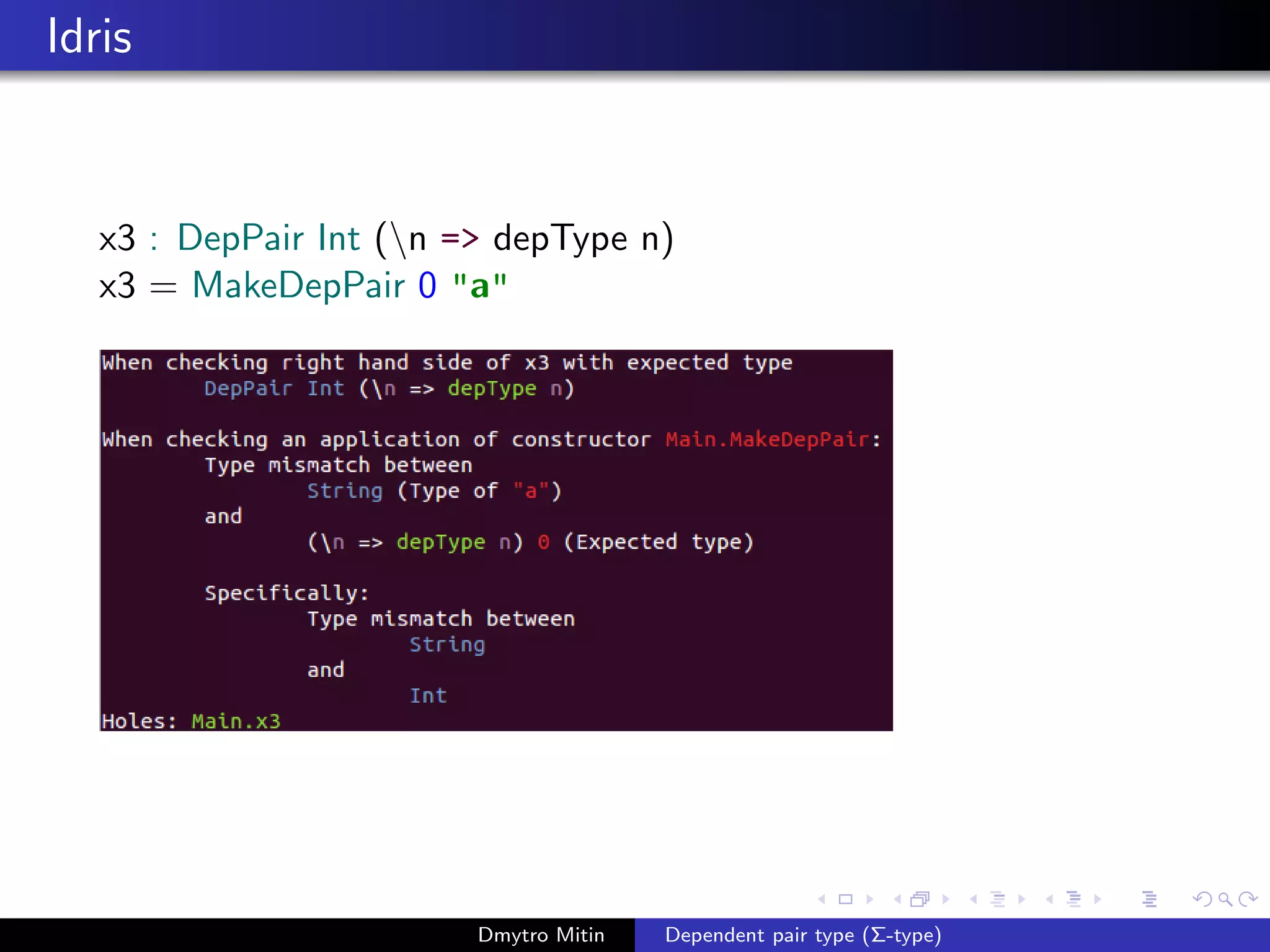
8. Scala
sealed trait Nat {
type This >: this.type <: Nat
type ++ = Succ[This]
}
final object Zero extends Nat {
type This = Zero
}
type Zero = Zero.type
final class Succ[N <: Nat] extends Nat {
type This = Succ[N]
}
Dmytro Mitin Dependent pair type (Σ-type)

9. Scala
type 0 = Zero
type 1 = 0 # ++
type 2 = 1 # ++
type 3 = 2 # ++
val 0: 0 = Zero
val 1: 1 = new Succ[ 0]
val 2: 2 = new Succ[ 1]
val 3: 3 = new Succ[ 2]
Dmytro Mitin Dependent pair type (Σ-type)

10. Scala
sealed trait DepType[N <: Nat] { type T }
implicit object depType0 extends DepType[ 0] { type T = Int }
implicit object depType1 extends DepType[ 1] { type T = String }
implicit def depType[N <: Nat] = new DepType[Succ[Succ[N]]] {
type T = Boolean }
case class DepPair[N <: Nat, V](x: N, value: V)(implicit
depType: DepType[N] { type T = V })
DepPair( 0, 10)
DepPair( 1, "aaa")
DepPair( 2, true)
DepPair( 2, "bbb") // error
DepPair( 3, false)
Dmytro Mitin Dependent pair type (Σ-type)

11. ProvingGround. Built-in type
git clone https://github.com/siddhartha-gadgil/ProvingGround.git
cd ProvingGround
sbt mantle/test:console
val A = "A" :: Type
val B = "B( : A)" :: A ->: Type
val a = "a" :: A
val b = "b" :: B(a)
val pair = mkPair(a, b) !: Sgma(a !: A, B(a))
val recSABA = Sgma(a !: A, B(a)).rec(A)
val first = recSABA(a :∼> (b :-> a))
first(pair) == a
val recSABSAB = Sgma(a !: A, B(a)).rec(Sgma(a !: A, B(a)))
val id = recSABSAB(a :∼> (b :->
mkPair(a, b).asInstanceOf[DepPair[Term, Term]]))
id(pair) == pair
Dmytro Mitin Dependent pair type (Σ-type)

12. ProvingGround. Custom type
import TLImplicits.
import shapeless.
val A = "A" :: Type
val B = "B( : A)" :: A ->: Type
val a = "a" :: A
val b = "b" :: B(a)
val SigmaAB = "Sigma(a : A, B(a))" :: Type
val SigmaInd = ("mkPair" ::: a ∼>>: (B(a) ->>: SigmaAB))
=: SigmaAB
val makePair :: HNil = SigmaInd.intros
val pair = makePair(a)(b) !: SigmaAB
val recSABA = SigmaInd.rec(A)
val first = recSABA(a :∼> (b :-> a))
first(pair) == a
val recSABSAB = SigmaInd.rec(SigmaAB)
val id = recSABSAB(a :∼> (b :-> makePair(a)(b)))
id(pair) == pair
Dmytro Mitin Dependent pair type (Σ-type)