This document summarizes a presentation about type classes in Scala. It introduces type classes like Monoid and Functor. It provides examples of Monoid instances for types like Int and Option. It explains how to define type classes for new types. It shows how to generalize functions like sequence and traverse to work for any Applicative functor using type classes. Finally, it discusses related concepts like Semigroup, Semigroupal functors, and NonEmptyList.

1. Oh, All the things you’ll traverse
ScalaDays - Luka Jacobowitz

2. Software Developer at
codecentric
Co-organizer of ScalaDus
and IdrisDus
Maintainer of cats,
cats-effect, cats-mtl,
OutWatch
Enthusiastic about FP
About me

3. ● Type classes
● Monoids
● Functors
● Traversals
Agenda

4. Type classes ● Type classes offer us
ad-hoc polymorphism
● Operate on types rather
than instances
● Pretty similar to OOP
interfaces (traits)
● No explicit language
support in Scala... (yet)

5. A small type class example
@typeclass
trait Show[T] {
def show(value: T): String
}
implicit val showString: Show[String] = new Show[String] {
def show(value: String): String = value
}
implicit val showInt: Show[Int] = _.toString
def emptyIfFalse[T: Show](t: T, f: T => Boolean): String =
if (f(t)) t.show else “”

6. Something a bit more useful
@typeclass
trait Monoid[T] {
def empty: T
def combine(a: T, b: T): T
}
implicit val monoidInt: Monoid[Int] = new Monoid[Int] {
def empty: Int = 0
def combine(a: Int, b: Int): Int = a + b
}

7. Something a bit more useful
def sumInt(list: List[Int]): Int =
list.foldLeft(0)(_ + _)
def sumString(list: List[String]): String =
list.foldLeft("")(_ + _)
def sumSet[T](list: List[Set[T]]): Set[T] =
list.foldLeft(Set.empty[T])(_ union _)
def sum[T: Monoid](list: List[T]): T =
list.foldLeft(Monoid[T].empty)(_ combine _)

8. Something a bit more useful
def sumInt(list: List[Int]): Int =
list.foldLeft(0)(_ + _)
def sumString(list: List[String]): String =
list.foldLeft("")(_ + _)
def sumSet[T](list: List[Set[T]]): Set[T] =
list.foldLeft(Set.empty[T])(_ union _)
def sum[T: Monoid](list: List[T]): T =
list.foldLeft(Monoid[T].empty)(_ combine _)

9. Implicit derivation
implicit def optionMonoid[T: Monoid] = new Monoid[Option[T]] {
def empty = None
def combine(a: Option[T], b: Option[T]) = (a, b) match {
case (Some(x), Some(y)) => Some(x |+| y)
case (Some(x), None) => Some(x)
case (None, Some(y)) => Some(y)
case (None, None) => None
}
}

10. Type classes vs subtyping
● Type classes give us operations on types instead of on values
● This comes in handy when dealing with type classes like Monoids
● We can use type classes to derive instances for data types that
might hold other data types when they also have instances.

11. Monoids everywhere
implicit def functionMonoid[A, B: Monoid] = new Monoid[A => B] {
def empty = _ => Monoid[B].empty
def combine(x: A => B, y: A => B): A => B =
a => x(a) |+| y(a)
}
implicit def tupleMonoid[A: Monoid, B: Monoid] = new Monoid[(A, B)] {
def empty = (Monoid[A].empty, Monoid[B].empty)
def combine(x: (A, B), y: (A, B)): (A, B) =
(x._1 |+| y._1, x._2 |+| y._2)
}

12. Monoids everywhere
implicit def eitherMonoid[A, B: Monoid]: Monoid[Either[A, B]]
implicit def mapMonoid[A, B: Monoid]: Monoid[Map[A, B]]
implicit def futureMonoid[A: Monoid]: Monoid[Future[A]]
And many more!

13. Monoids applied
def step(word: String) = (1, word.length, Map(word -> 1))
val data = lines.flatMap(_.split(" ").toList).map(step)
val empty = Monoid[(Int, Int, Map[String, Int])].empty
val (words, chars, wordCount) = data.foldLeft(empty)(_ |+| _)

14. Monoids applied
def step(word: String) = (1, word.length, Map(word -> 1))
val data = lines.flatMap(_.split(" ").toList).map(step)
val (words, chars, wordCount) = data.combineAll

15. Monoids applied
def step(word: String) = (1, word.length, Map(word -> 1))
val data = lines.flatMap(_.split(" ").toList).map(step)
val (words, chars, wordCount) = data.combineAll
list.combineAll === list.foldLeft(empty)(_ |+| _)

16. Monoid laws
1. Associativity:
(x |+| y) |+| z === x |+| (y |+| z)
2. Right identity:
x |+| empty === x
3. Left identity:
empty |+| x === x

17. Monoid laws in action
(a |+| b |+| c |+| d |+| e |+| f |+| g)
↕
(a |+| b) |+| (c |+| d) |+| (e |+| f) |+| g
↕
(a |+| b) |+| (c |+| d) |+| (e |+| f) |+| (g |+| empty)
We can write a fully parallel version of fold!!

18. Parallel fold
val grouped: List[List[A]] =
list.grouped(getRuntime.availableProcessors)
val innerFolded: List[A] =
grouped.parallelMap(_.combineAll)
val result: A =
innerFolded.combineAll

19. Let’s talk about Functors
@typeclass
trait Functor[F[_]] {
def map[A, B](fa: F[A])(f: A => B): F[B]
}
List(1, 2, 3).map(_.toString)
Option(42).map(_.toString)
Right(23).map(_.toString)
Vector(-1, 39, 11).map(_.toString)
Future(22).map(_.toString)

20. Let’s talk about Monoidal Functors
(A |+| A): A
(F[A] |+| F[A]): F[A]
(F[A] |@| F[B]): F[???]

21. Let’s talk about Monoidal Functors
(A |+| A): A
(F[A] |+| F[A]): F[A]
(F[A] |@| F[B]): F[(A, B)]

22. Let’s talk about Monoidal Functors
@typeclass
trait Monoidal[F[_]] extends Functor[F] {
def product[A, B](fa: F[A], fb: F[B]): F[(A, B)]
def pure[A](a: A): F[A]
}
implicit val optionMonoidal: Monoidal[Option]
implicit val futureMonoidal: Monoidal[Future]

23. Generalizing Future.sequence
object Future {
def sequence[A](l: List[Future[A]]): Future[List[A]]
}

24. Generalizing Future.sequence
def sequence[A](l: List[Future[A]]): Future[List[A]]
def sequence[F[_]: Monoidal, A](l: List[F[A]]): F[List[A]] =
l.foldRight(Monoidal[F].pure(List.empty[A]))
{ (fa: F[A], acc: F[List[A]]) =>
val prod: F[(A, List[A])] = fa.product(acc)
prod.map(_ +: _)
}

25. Generalizing Future.sequence
def sequence[A](l: List[Future[A]]): Future[List[A]]
def sequence[F[_]: Monoidal, A](l: List[F[A]]): F[List[A]] =
l.foldRight(Monoidal[F].pure(List.empty[A]))
{ (fa: F[A], acc: F[List[A]]) =>
val prod: F[(A, List[A])] = fa.product(acc)
prod.map(_ +: _)
}

26. Generalizing Future.sequence
def sequence[A](l: List[Future[A]]): Future[List[A]]
def sequence[F[_]: Monoidal, A](l: List[F[A]]): F[List[A]] =
l.foldRight(Monoidal[F].pure(List.empty[A]))
{ (fa: F[A], acc: F[List[A]]) =>
(fa, acc).mapN(_ +: _)
}

27. Generalizing Future.sequence
def sequence[A](l: List[Future[A]]): Future[List[A]]
def sequence[F[_]: Monoidal, A](l: List[F[A]]): F[List[A]] =
l.foldRight(Monoidal[F].pure(List.empty[A]))
{ (fa: F[A], acc: F[List[A]]) =>
(fa, acc).mapN(_ +: _)
}
fa.product(fb).map(f) === (fa, fb).mapN(f)

28. Generalizing Future.traverse
def traverse[A, B](l: List[A])(f: A => Future[B]): Future[List[B]]
def traverse[F[_]: Monoidal, A, B](l: List[A])(f: A => F[B]): F[List[B] =
l.foldRight(Monoidal[F].pure(List.empty[B]))
{ (a: A, acc: F[List[B]]) =>
(acc, f(a)).mapN(_ :+ _)
}
l.traverse(f) === l.map(f).sequence

29. The laws remain the same
1. Associativity:
(fa product fb) product fc ~ fa product (fb product fc)
2. Right identity:
fa product pure(()) ~ fa
3. Left identity:
pure(()) product fa ~ fa

30. A tiny secret
What we called Monoidal so far, is usually called Applicative in
programmer’s circles.
I personally think Monoidal is the better name as it describes the
relationship to Monoids much better, but for the sake of consistency
we’ll use Applicative.

31. The Foldable type class
So far we used List everywhere, but what about Vector, Stream, etc?
@typeclass
trait Foldable[F[_]] {
def foldMap[A, M: Monoid](fa: F[A])(f: A => M): M
def combineAll[M: Monoid](fa: F[M]): M = foldMap(identity)
}
implicit val listFoldable: Foldable[List]
implicit def vectorFoldable: Foldable[Vector]
implicit def optionFoldable: Foldable[Option]

32. The Traverse type class
@typeclass
trait Traverse[T[_]] extends Foldable[T] with Functor[T] {
def sequence[F[_]: Applicative, A](tfa: T[F[A]]): F[T[A]]
def traverse[F[_]: Applicative, A, B](ta: T[A], f: A => F[B]): F[T[B]]
}
implicit def vectorTraversable: Traverse[Vector]
implicit def optionTraversable: Traverse[Option]
type EitherString[A] = Either[String, A]
implicit def eitherStringTraversable: Traverse[EitherString]

33. The Traverse type class
@typeclass
trait Traverse[T[_]] extends Foldable[T] with Functor[T] {
def sequence[F[_]: Applicative, A](tfa: T[F[A]]): F[T[A]]
def traverse[F[_]: Applicative, A, B](ta: T[A], f: A => F[B]): F[T[B]]
}
implicit def vectorTraversable: Traverse[Vector]
implicit def optionTraversable: Traverse[Option]
implicit def eitherStringTraversable[E]: Traverse[Either[E, ?]]

34. The Traverse type class
List[Future[A]] => Future[List[A]]
Stream[Option[A]] => Option[Stream[A]]
Either[E, IO[A]] => IO[Either[E, A]]
Vector[ValidatedNel[Error, A]] => ValidatedNel[Error, Vector[A]]

35. ValidatedNel???
sealed trait Validated[+E, +A]
case class Valid[+A](a: A) extends Validated[Nothing, A]
case class Invalid[+E](e: E) extends Validated[E, Nothing]
type ValidatedNel[E, A] = Validated[NonEmptyList[E], A]
def validate(u: String): ValidatedNel[Error, User]
val users: ValidatedNel[Error, List[User]] = lines.traverse(validate)

36. Still not convinced?

37. Still not convinced?

38. Still not convinced?

39. Still not convinced?

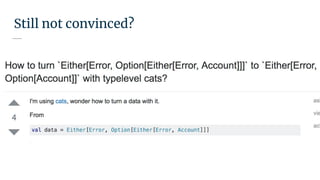
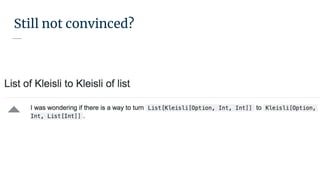
40. Bonus: Semigroups!
@typeclass
trait Semigroup[T] {
def combine(a: T, b: T): T
}
Semigroups describe an associative binary operation.
@typeclass
trait Monoid[T] extends Semigroup[T] {
def empty: T
}

41. Bonus: Semigroups!
List().max
// java.lang.UnsupportedOperationException: empty.max
List().reduce(_ |+| _)
// java.lang.UnsupportedOperationException: empty.reduceLeft
NonEmptyList()
// not enough arguments for method apply: (head: A, tail: A*)
NonEmptyList(1, 2).maximum
// res0: Int = 2
NonEmptyList(1, 2, 3, 4).reduce(_ |+| _)
// res1: Int = 7

42. … and Semigroupal Functors!
@typeclass
trait Semigroupal[F[_]] extends Functor[F] {
def product[A, B](fa: F[A], fb: F[B]): F[(A, B)]
}
@typeclass
trait Monoidal[F[_]] extends Semigroupal[F] {
def pure[A](a: A): F[A]
}

43. … and Semigroupal Functors!
@typeclass
trait Apply[F[_]] extends Functor[F] {
def product[A, B](fa: F[A], fb: F[B]): F[(A, B)]
}
@typeclass
trait Applicative[F[_]] extends Semigroupal[F] {
def pure[A](a: A): F[A]
}

44. … and Semigroupal Functors!
implicit def mapApplicative[K] = new Applicative[Map[K, ?]] {
def pure[V](v: V): Map[K, V] = ???
// ...
}
It doesn’t work!
implicit def mapApply[K] = new Apply[Map[K, ?]] {
// ...
}
This does! :)

45. Conclusions
Today, we learned about Monoids, Functors,
Monoidal/Applicative Functors and Foldables.
We also learned about NonEmptyLists and Validated.
And of course, we learned about the almighty power of
traverse!
I Hope this was a good gateway drug to the cats library.

46. Thank you for
listening!
Twitter: @LukaJacobowitz
GitHub: LukaJCB