This document provides an overview of algebraic structures like monoids, lattices, groups, and rings. It discusses how these concepts can be generalized to higher-kinded type classes in Scala. It also explores how Scala's type system relates to these structures, with sum and product types forming commutative rigs. Finally, it discusses how these structures can be useful for modeling parallelism, error handling, and other programming patterns in Scala.

1. Monoids, Monoids, Monoids
A fun ride through Abstract Algebra and Type Theory

2. Software Engineer at
CompStak
Maintainer of various
Typelevel libraries
Enthusiastic about FP
About me

3. ● Monoids
● Monoids
● Monoids
● Monoids
Agenda

4. ● Monoids
● Abstract Algebra
● Type Theory
Agenda

5. Monoids - Intro
trait Monoid[A] {
def empty: A
def combine(x: A, y: A): A
}
implicit val monoidInt: Monoid[Int] = new Monoid[Int] {
def empty: Int = 0
def combine(a: Int, b: Int): Int = a + b
}

6. Monoids
def combineInts(list: List[Int]): Int =
list.foldLeft(0)(_ + _)
def combineStrings(list: List[String]): String =
list.foldLeft("")(_ + _)
def combineSets[T](list: List[Set[T]]): Set[T] =
list.foldLeft(Set.empty[T])(_ union _)
def combineAll[T: Monoid](list: List[T]): T =
list.foldLeft(Monoid[T].empty)(_ combine _)

7. Monoids everywhere
implicit def functionMonoid[A, B: Monoid] = new Monoid[A => B]
implicit def optionMonoid[A: Monoid]: Monoid[Option[A]]
implicit def tupleMonoid[A: Monoid, B: Monoid] = new Monoid[(A, B)]
implicit def mapMonoid[A, B: Monoid]: Monoid[Map[A, B]]
implicit def ioMonoid[A: Monoid]: Monoid[IO[A]]
And many more!

8. Monoids applied
def step(word: String) = (1, word.length, Map(word -> 1))
val (words, chars, occurences) = data.foldMap(step)
val result = stream.scanMap(step)

9. Monoid laws
1. Associativity:
(x |+| y) |+| z === x |+| (y |+| z)
2. Right identity:
x |+| empty === x
3. Left identity:
empty |+| x === x

10. Associativity in action
(a |+| b |+| c |+| d |+| e |+| f |+| g)
↕
(a |+| b) |+| (c |+| d) |+| (e |+| f) |+| g
We can fully parallelize any associative operation!

11. Parallel aggregation
val stream: Stream[IO, A] = ...
val maxParallel: Int = getRunTime.availableProcessors
val result: IO[A] = stream.chunks
.mapAsync(maxParallel)(_.combineAll.pure[IO])
.compile
.foldMonoid

12. Algebraic laws
● Associativity
● Identity
● Invertibility
● Commutativity
● Idempotency
● Absorption
● Distributivity

13. cats-kernel

14. cats-kernel

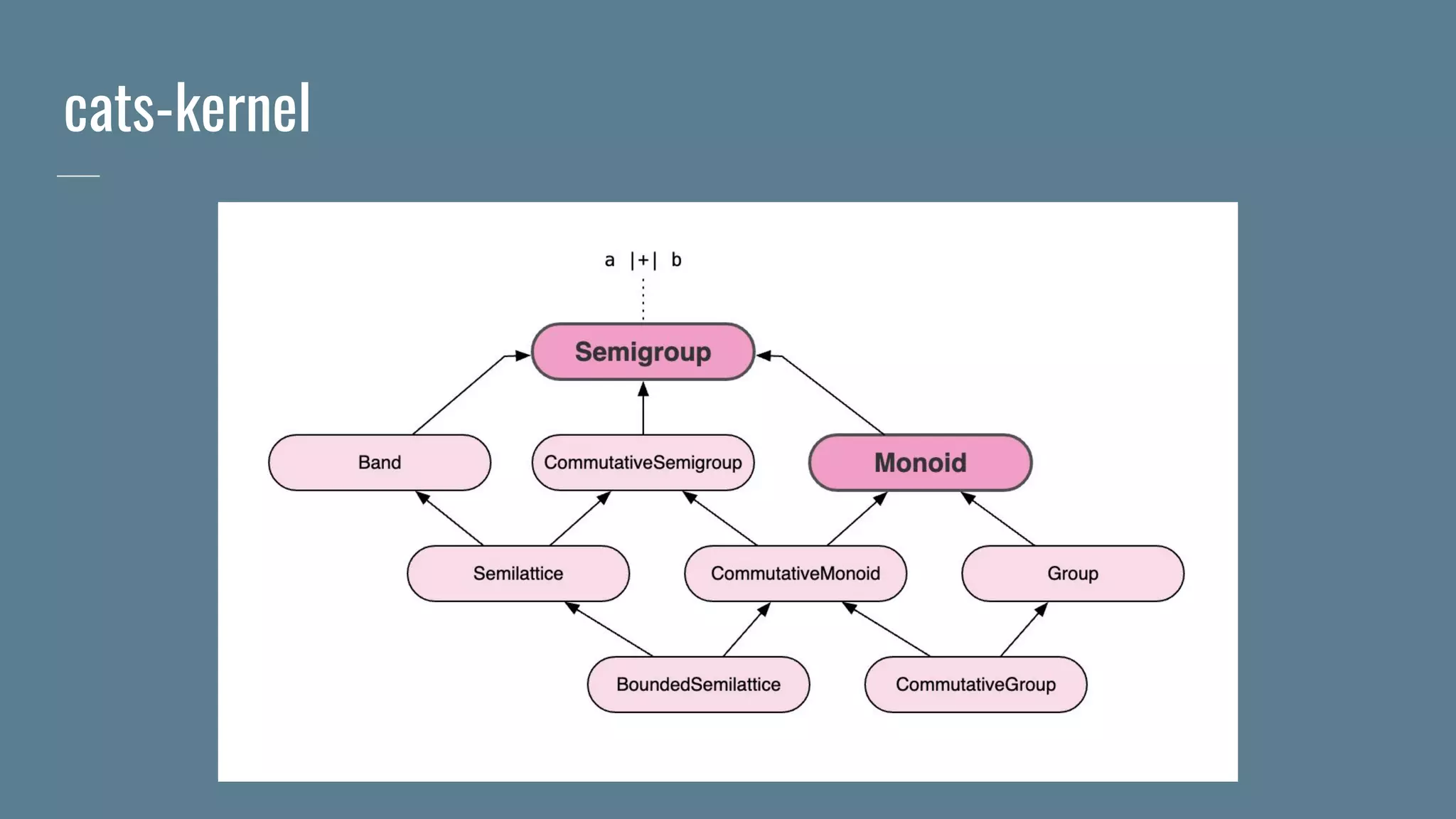
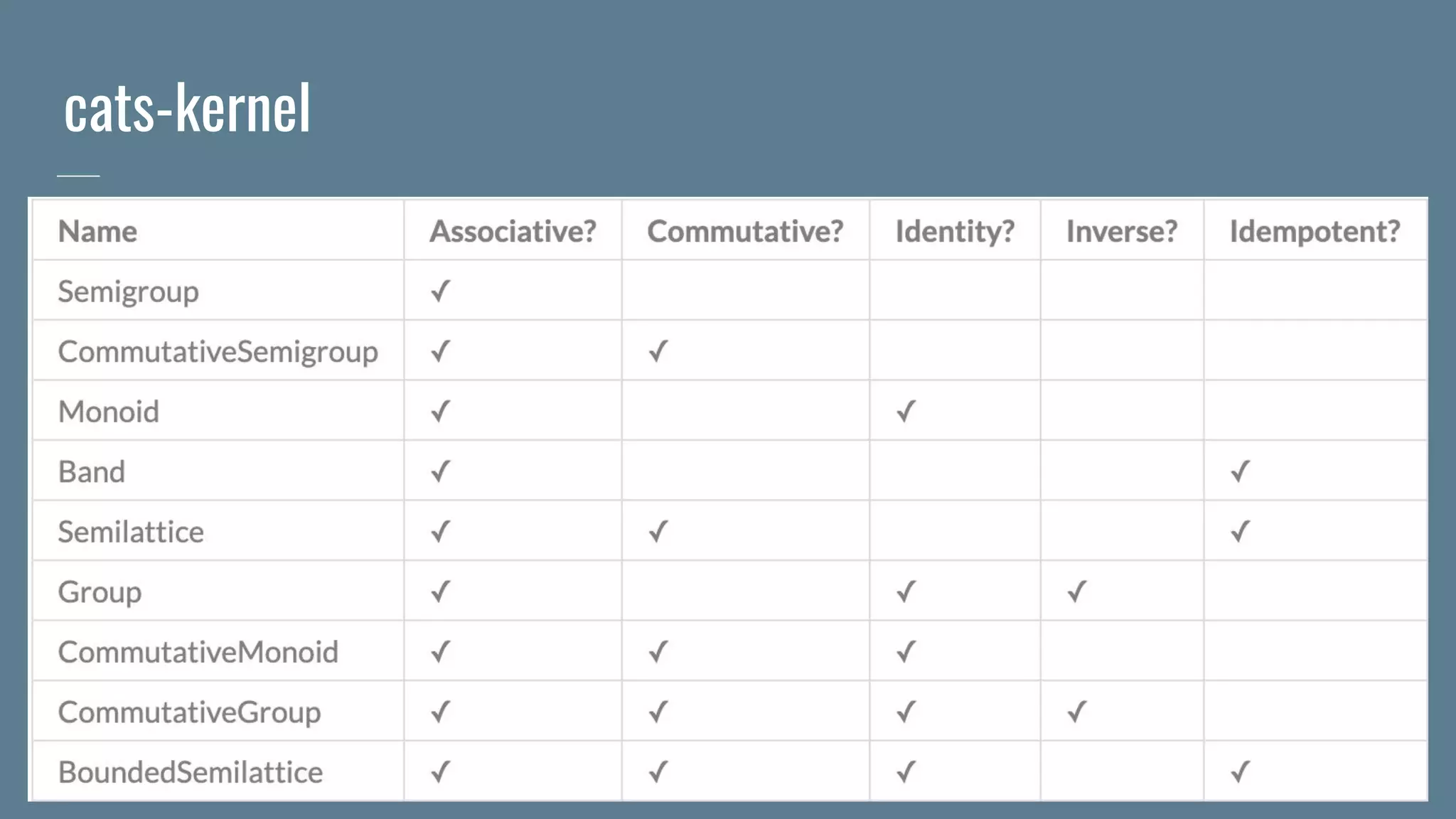
15. Groups
trait Group[A] extends Monoid[A] {
def inverse(a: A): A
}
a |+| inverse(a) === empty
inverse(a) |+| a === empty
5 + (-5) === 0
4 * (¼) === 1
Set(1,2,3) symmetricDiff Set(1,2,3) === Set()

16. Groups

17. Groups
sealed trait NList[+A]
case class Add[A](a: A) extends NList[A]
case class Remove[A](a: A) extends NList[A]
case object Empty extends NList[Nothing]
case class Concat[A](x: NList[A], y: NList[A]) extends NList[A]

18. Semilattices
trait Semilattice[A] extends CommutativeSemigroup[A]
a |+| a === a
true && true === true
false && false === false
true || true === true
Set(1,2,3) union Set(1,2,3) === Set(1,2,3)
Set(1,2,3) intersect Set(1,2,3) === Set(1,2,3)
max(7, 7) === 7

19. Semilattices
Use cases:
● Consuming messages with At-Least-Once Delivery
● Independently updating state in a distributed System (CRDTs)
● Any situation you might need idempotency

20. cats-kernel

21. Algebraic laws
● Associativity ✅
● Identity ✅
● Invertibility ✅
● Commutativity ✅
● Idempotency ✅
● Absorption
● Distributivity

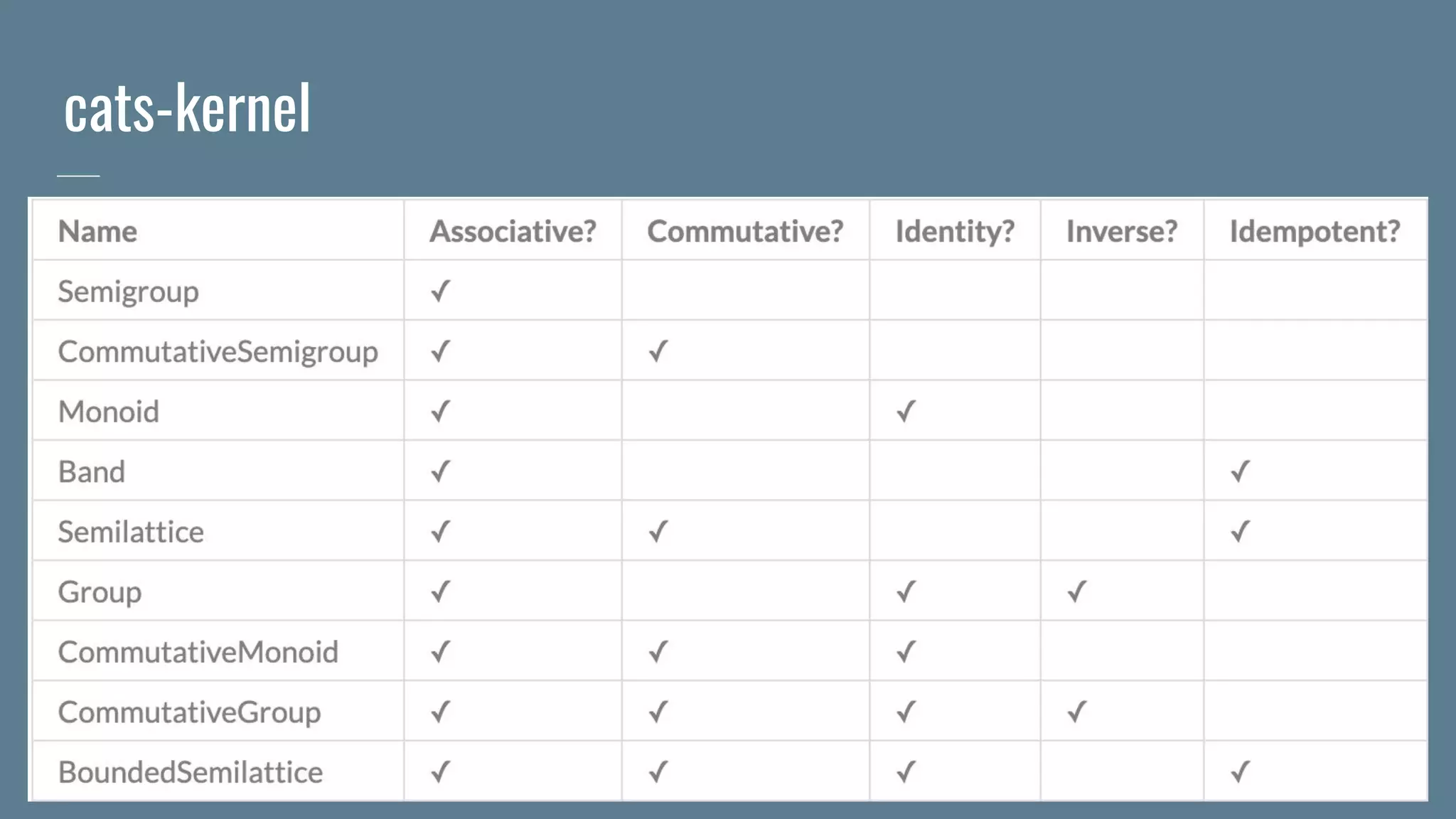
22. Ring-like structures
trait Semiring[A] {
def plus(x: A, y: A): A
def times(x: A, y: A): A
def zero: A
}
plus forms a commutative Monoid with zero as an identity
times forms a Semigroup
zero “absorbs” times:
a * 0 === 0
times “distributes” over plus:
a * (b + c) === (a * b) + (a * c)

23. Ring-like structures
Commutative additive monoid & multiplicative semigroup => Semiring
Commutative additive group & multiplicative semigroup => Rng
Commutative additive monoid & multiplicative monoid => Rig
Commutative additive group & multiplicative monoid => Ring
Commutative additive group & multiplicative group => Field

24. Lattices
Two Semilattices on the same type => Lattice
Two bounded Semilattices => Bounded Lattice
Two Semilattices that distribute over another => Distributive Lattice
Two bounded Semilattices that distribute over another =>
Bounded distributive Lattice

25. Monoids at the typelevel
So far we’ve talked about algebraic structures at the value level, but
in Scala we encounter them at the typelevel as well.

26. Product types are monoids
Associativity law:
(A, (B, C)) <-> ((A, B), C)
Identity laws:
(A, Unit) <-> A
(Unit, A) <-> A
Akin to the cartesian product of the set of inhabitants of the two types

27. Product types are monoids

28. Product types are monoids

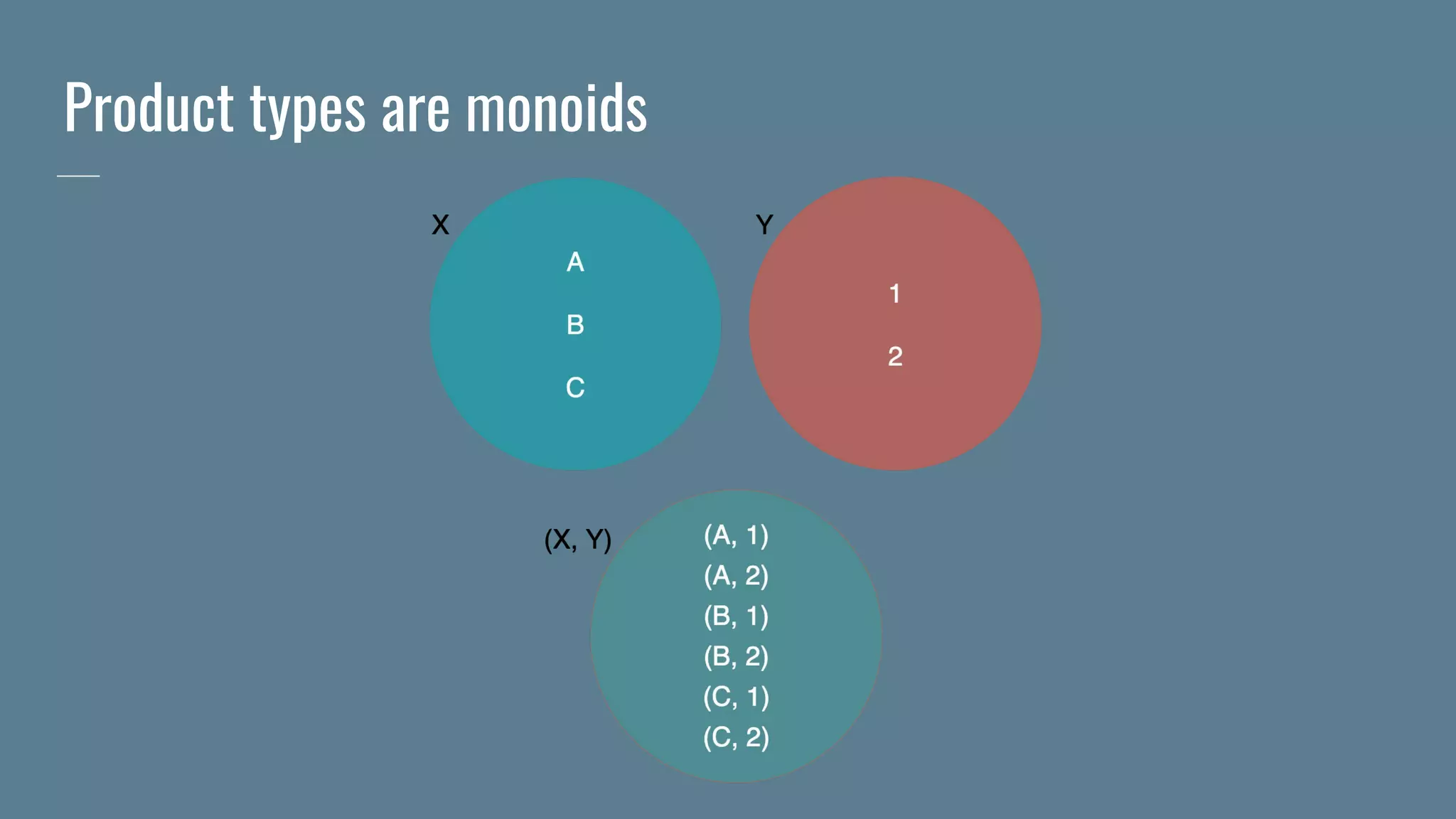
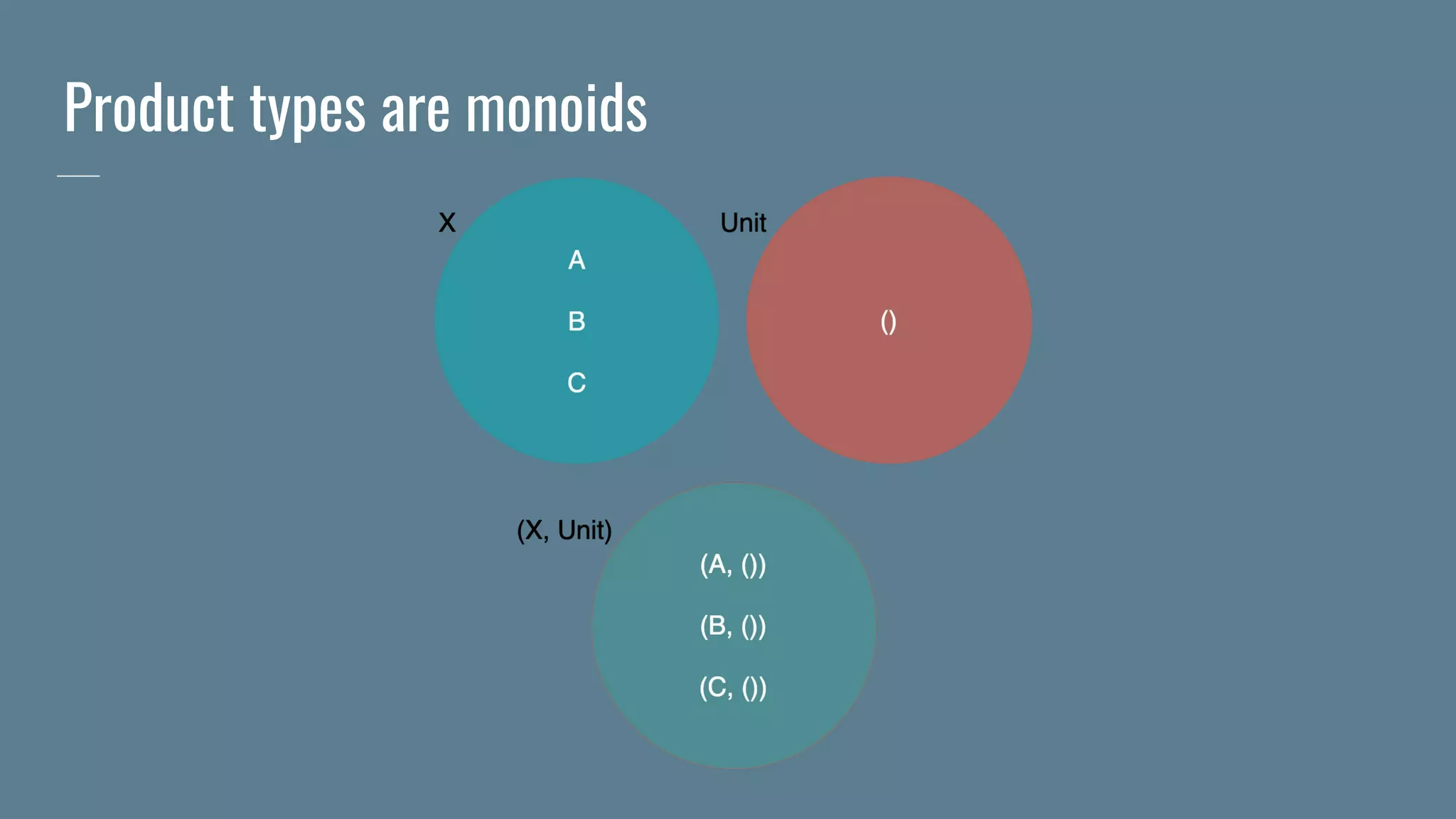
29. Sum types are monoids
Associativity law:
Either[A, Either[B, C]] <-> Either[Either[A, B], C]
Identity laws:
Either[A, Nothing] <-> A
Either[Nothing, A] <-> A
Akin to the disjoint union of the set of inhabitants of the two types

30. Sum types are monoids

31. Sum types are monoids

32. How is this relevant?
trait Semigroupal[F[_]] {
def product[A, B](fa: F[A], fb: F[B]): F[(A, B)]
}
An abstract higher kinded semigroup, that merges two contexts inside a
product type.
trait Apply[F[_]] extends Semigroupal[F] with Functor[F] {
def ap[A, B](fa: F[A])(f: F[A => B]): F[B]
def product[A, B](fa: F[A])(fb: F[B]): F[(A, B)] =
ap(fa)(fb.map(b => a => (a, b)))
}

33. Apply is a Semigroupal functor
trait Monoidal[F[_]] extends Semigroupal[F] {
def unit: F[Unit]
}
An abstract higher kinded monoid, that uses the product type identity as
its own identity
trait Applicative[F[_]] extends Apply[F] with Monoidal[F] {
def pure[A](a: A): F[A]
def unit: F[Unit] =
pure(())
}

34. We can do the same with sum types
trait SumSemigroupal[F[_]] {
def sum[A, B](fa: F[A], fb: F[B]): F[Either[A, B]]
}
trait SumMonoidal[F[_]] extends SumSemigroupal[F] {
def nothing: F[Nothing]
}
An abstract higher kinded monoid, that merges two contexts inside a sum
type.

35. We can do the same with sum types
trait SemigroupK[F[_]] {
def sum[A, B](fa: F[A], fb: F[B]): F[Either[A, B]]
def combineK[A](x: F[A], y: F[A]): F[A] =
sum(x, y).map(_.merge)
}
trait MonoidK[F[_]] extends SemigroupK[F] {
def empty[A]: F[A]
}

36. Monoids for iteration
def foldMap[A, M: Monoid](fa: F[A])(f: A => M): M
def foldMapK[G[_]: MonoidK, A, B](fa: F[A])(f: A => G[B]): G[B]
def traverse[G[_]: Applicative, A, B](l: F[A])(f: A => G[B]): G[F[B]]
def foldMapM[G[_]: Monad, A, B: Monoid](fa: F[A])(f: A => G[B]): G[B]

37. Different formulation of the same laws
Monoid laws:
x |+| (y |+| z) === (x |+| y) |+| z
empty |+| x === x
Applicative laws:
a *> (b *> c) === (a *> b) *> c
pure(()) *> a === a
MonoidK laws:
a <+> (b <+> c) === (a <+> b) <+> c
empty <+> a === a
Monad laws:
fa >>= (a => f(a) >>= g) === (fa >>= f) >>= g
pure(()) >>= (_ => fa) === fa

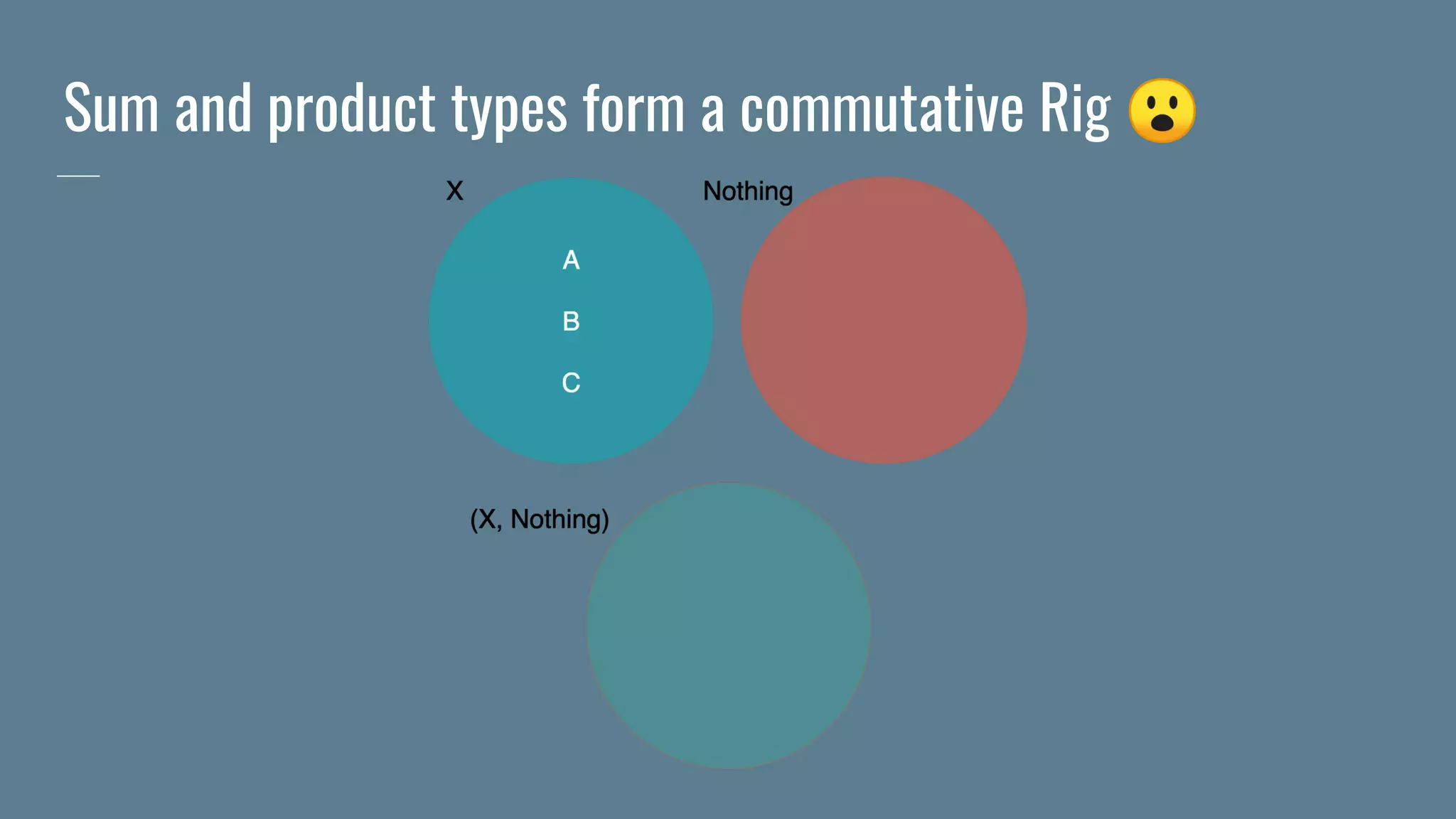
38. Sum and product types form a commutative Rig 😮
type +[A, B] = Either[A, B]
type *[A, B] = (A, B)
type Zero = Nothing
type One = Unit
Absorption law:
A * Zero <-> Zero
Distributivity law:
A * (B + C) <-> (A * B) + (A * C)
Commutativity laws:
A + B <-> B + A
A * B <-> B * A

39. Sum and product types form a commutative Rig 😮

40. Alternative is a higher kinded Rig
trait Alternative[F[_]] {
def sum[A, B](fa: F[A], fb: F[B]): F[Either[A, B]]
def product[A, B](fa: F[A], fb: F[B]): F[(A, B)]
def pure[A](a: A): F[A]
def empty[A]: F[A]
}

41. Union types are bounded semilattices
Associativity law:
A | (B | C) =:= (A | B) | C
Identity law:
A | Nothing =:= A
Commutativity law:
A | B =:= B | A
Idempotency law:
A | A =:= A
Akin to the union of the set of inhabitants of the two types

42. Different equivalence relations
A =:= A | A
A <-> (A, Unit)

43. Difference between sum types and union types

44. Union types are bounded semilattices

45. Intersection types are bounded semilattices
Associativity law:
A & (B & C) =:= (A & B) & C
Identity law:
A & Any =:= A
Commutativity law:
A & B =:= B & A
Idempotency law:
A & A =:= A
Akin to the intersection of the set of inhabitants of the two types

46. Intersection types are bounded semilattices

47. Intersection types are bounded semilattices

48. Union and intersection types form a bounded distributive lattice 😮
Idempotency law:
A | A =:= A
A & A =:= A
Absorption laws:
A | Any =:= Any
A & Nothing =:= Nothing
Distributivity laws:
A | (B & C) =:= (A | B) & (A | C)
A & (B | C) =:= (A & B) | (A & C)

49. Union and intersection types form a bounded distributive lattice 😮

50. Union and intersection types form a bounded distributive lattice 😮

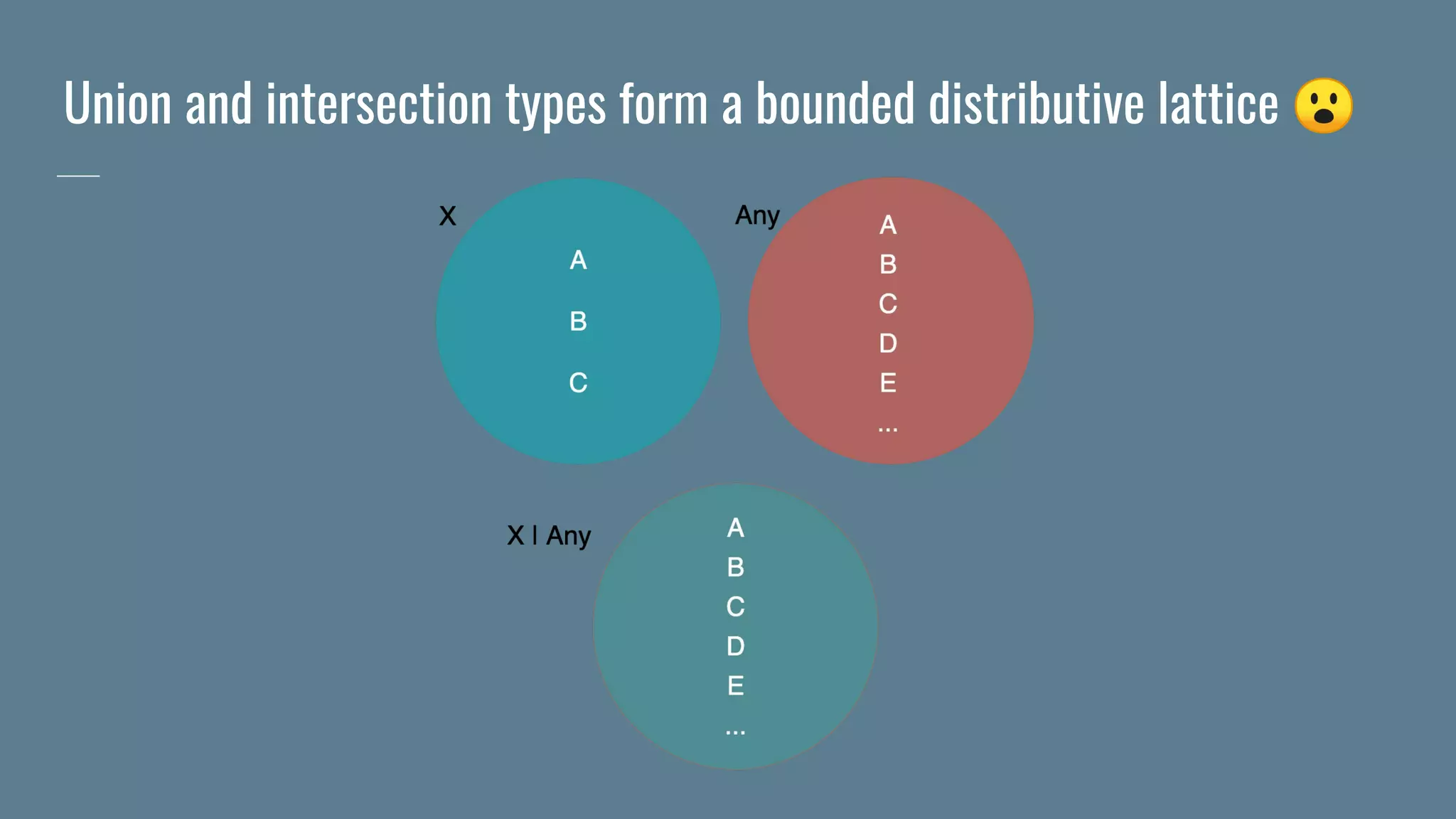
51. How is this useful?
trait UnionMonoidal[F[_]] extends Functor[F] {
def union[A, B](fa: F[A], fb: F[B]): F[A | B]
def empty[A]: F[A]
def combineK[A](x: F[A], y: F[A]): F[A] =
union(x, y)
def sum[A, B](fa: F[A], fb: F[B]): F[Either[A, B]] =
combineK(map(fa)(Left(_)), map(fb)(Right(_)))
}

52. How is this useful?
Either[Unit, A] <-> Option[A]
Either[Nothing, A] <-> A
(A, Unit) <-> A
ApplicativeError[F, Unit] ⇔ Alternative[F]
MonadError[F, Nothing] ⇔ Monad[F]
MonadWriter[F, Unit] ⇔ Monad[F]

53. How is this useful?
sealed trait GList[+A, +B] {
def head: A | B = ...
}
case class Nil[B](b: B) extends GList[Nothing, B]
// ...
type List[A] = GList[A, Unit]
type NonEmptyList[A] = GList[A, Nothing]

54. Other cool stuff
● MonadError is two monoids (monads) based on Either
● Parallel is two monoids with the same identity, so 0=1 (apparently
called a duoid, or united monoid)
● Categories are monoids too
● Cats-retry’s RetryPolicy is a Bounded Distributive Lattice
● Animations (Sequence and Parallel)

55. Conclusions
Today, we learned about different algebraic structures like
monoids, lattices, groups and rings and how we can use
higher kinded type classes to generalize some of these
concepts.
We also learned about some basic properties about Scala’s
type system and how it relates to these algebraic
structures.
Lastly, we also looked at some of the changes made to the
type system in the upcoming Scala 3 release.

56. We’re hiring!

57. Thank you for
listening!
Twitter: @LukaJacobowitz
GitHub: LukaJCB