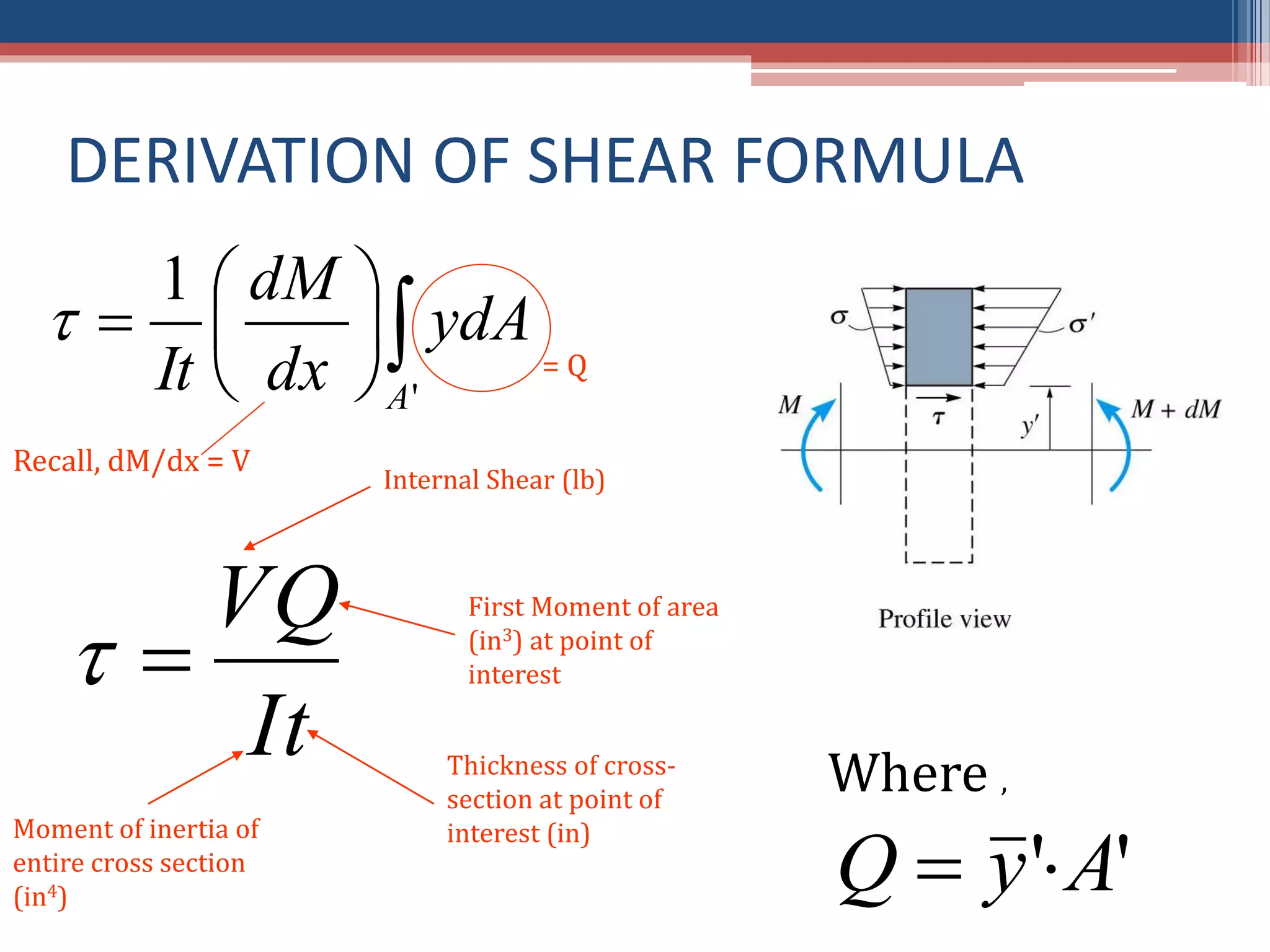
This document derives the formula for shear stress distribution in a square cross-section beam. It begins by introducing shear stress and normal stress. It then shows the derivation of the shear stress formula using integrals and the relationship between shear force and shear stress. The formula derived is that shear stress varies quadratically with distance from the neutral axis, reaching a maximum at the center of the cross-section and reducing to zero at the outer edges. For a square cross-section, the final formula is that shear stress equals the shear force times (b^2/4 - y1^2)/2I, where b is the side length and y1 is the distance from the neutral axis.

1. MOS GD
SHEAR STRESS DISTRIBUTION
FOR SQUARE CROSS-SECTION
PRESENTED BY-
NEERAJ GAUTAM
ROLL NO. 144152
Batch – M 2

2. INTRODUCTION
We determine the normal stress and shear stress on a body
or a beam or a structure to design of the beams or structures.
• When a beam is in pure bending, the only stress are the normal stresses
acting on the cross-section.
• When a beam is in non-uniform bending, both normal and shear stresses
are developed in the beam.
We have different cross-section (i.e. rectangular, circular webs of beams
with flanges, I sections) over which we determine the normal forces and
shear stress so that the proper design of beam or structure can be done
under required load.
Shear stress – Stresses which are applied along the surface of
the body is called shear stress.
It is represented by ‘τ’
τ
τ
τ
τ

3. DERIVATION OF SHEAR FORMULA
0

  xF
0)('
' '
  tdxdAdA
A A

0)(
' '











 
  tdxydA
I
M
dAy
I
dMM
A A

Consider the section shown in figure. To derive
the formula for shear stress , we first derive the
formula for shear force.

4. DERIVATION OF SHEAR FORMULA
It
VQ

Internal Shear (lb)
First Moment of area
(in3) at point of
interest
Thickness of cross-
section at point of
interest (in)Moment of inertia of
entire cross section
(in4)
'' AyQ 
Where ,







'
1
A
ydA
dx
dM
It

= Q
Recall, dM/dx = V

5. Distribution of shear stresses
Consider the beam to have a cross section of width ‘b’ and height ‘h’ as
shown in the figure. The distribution of the shear stress throughout the
cross section can be determined by computing shear stress at an
arbitrary height ‘y’ from the neutral axis and then plotting this function
. Here the dark shaded area will be used for computing ‘τ’.

6. Q= b( h/2 - y1 )(y1 + ( h/2 – y1 )/2 )
Q = b( h2 /4 –y1
2)/2
As we know,
Q= ∫ y dA = ∫ y b dy = b( h2 /4 –y1
2)/2
Substituting the expression
for Q into the shear formula ,
we get ,
τ = V ( h2 /4 –y1
2)/2I
This equation shows that shear stresses
in rectangular beam vary quadratically
with the distance y1 from the neutral
Axis.
h/2
y1

7. Thus when plotted along the height of the beam, τ varies as shown in figure.
Note :
•Shear stress is zero when y1 = + h/2.
•Shear stress is maximum at y1 = zero(0).
And we have ,
Now for square cross section ,
h =b
Thus formula for distribution of shear stress will be,
τ = V ( b2 /4 –y1
2)/2I
Where A = b2

8. Distribution of shear stress is shown below :