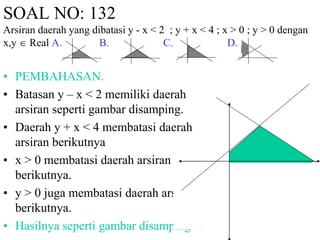
Dokumen tersebut berisi penjelasan dan pembahasan soal-soal matematika tentang konsep garis lurus, fungsi kuadrat, dan titik balik grafik fungsi. Diberikan 140 soal yang mencakup berbagai aspek terkait topik tersebut beserta penyelesaiannya secara rinci.

1. Oleh :
SUGENG RACHMONO,S.Pd..
2009

2. SOAL NO: 131
Tempat kedudukan daerah yang diarsir
A. {(x,y) / 1 < x < 5 } B. {(x,y) / 1 > y > 5 }
C. {(x,y) / 1 < x < 5 } D. {(x,y) / 1 > y > 5 }
• PEMBAHASAN.
• Daerah yang diarsir terdapat pada sistem koordinat
Cartesius.
• Daerah yang diarsir dibatasi oleh garis X = 1 dengan
ketentuan setiap absis yang dimiliki titik – titik daerah
yang diarsir tidak kurang dari 1 ( x > 1 ).
• Daerah yang diarsir dibatasi oleh garis X = 5 dengan
ketentuan setiap absis yang dimiliki titik – titik daerah
yang diarsir tidak lebih dari 5 ( x > 5 ).
• Daerah yang diarsir terletak pada X > 1 dan X < 5
• { (x,y) / 1 < x < 5 , x dan y bil Real }
X
Y
1 5

3. SOAL NO: 132
Arsiran daerah yang dibatasi y - x < 2 ; y + x < 4 ; x > 0 ; y > 0 dengan
x,y  Real A. B. C. D.
• PEMBAHASAN.
• Batasan y – x < 2 memiliki daerah
arsiran seperti gambar disamping.
• Daerah y + x < 4 membatasi daerah
arsiran berikutnya
• x > 0 membatasi daerah arsiran
berikutnya.
• y > 0 juga membatasi daerah arsiran
berikutnya.
• Hasilnya seperti gambar disamping 

4. SOAL NO: 133
Garis lurus yang melalui ( 4 , 1 ) dan ( - 2 , 1 ) memiliki gradiaen
……A. 0 B. – 2 C. 4 D. 7
• PEMBAHASAN.
• Garis lurus yang melalui dua titik memiliki rumus persamaan :
• y – y1 y2 – y1
• =
• x – x1 x2 – x1
• Garis lurus yang melalui ( 4, 1 ) dan (– 2, 1 ) memiliki persamaan :
• y – 1 1 – 1 y – 1
• =  = 0  y – 1 = 0
• x – 4 – 2 – 4 x – 4
• Garis y = 1 memiliki gradien = 0.
• 0.

5. SOAL NO: 134
Persamaan garis 3y = 6 - 2x mempunyai gradien …
A. 2 B. – 2 C. 2 / 3 D. – 2 / 3
• PEMBAHASAN.
• Persamaan garis 3y = 6 – 2x
• Dapat diubah menjadi y = 3 – 2/3 x
• Garis y = 3 – 2/3 x bergradien = – 2/3 .
• – 2/3 .

6. SOAL NO: 135
Persamaan garis pada gambar samping adalah :
A. y = – 2/5 x + 2 ; x,y  R
B. y = – 2/5 x – 2 ; x,y  R
C. y = – 5/2 x + 2 ; x,y  R
D. y = – 5/2 x – 2 ; x,y  R
• PEMBAHASAN.
• Garis lurus yang melalui dua titik memiliki rumus persamaan :
• y – y1 y2 – y1
• =
• x – x1 x2 – x1
• Persamaan garis lurus pada gambar melalui ( 0, 2 ) dan ( 5, 0 ) memiliki persamaan :
• y – 2 0 – 2
• =
• x – 0 5 – 0
• y – 2 – 2
•  = .
• x 5
•  y = – 2 / 5 x + 2
• y = – 2 / 5 x + 2
2
5

7. SOAL NO: 136
Persamaan garis pada gambar samping adalah :
A. 3x + 2y = 6 ; x,y  C
B. 2x + 3y = 6 ; x,y  C
C. 3x + 2y = 6 ; x,y  R
D. 2x + 3y = 6 ; x,y  R
• PEMBAHASAN.
• Garis lurus yang melalui dua titik memiliki rumus persamaan :
• y – y1 y2 – y1
• =
• x – x1 x2 – x1
• Persamaan garis lurus pada gambar melalui ( 0, 2 ) dan ( 3, 0 ) memiliki persamaan :
• y – 2 0 – 2
• =
• x – 0 3 – 0
• y – 2 – 2
•  = .
• x 3
•  3y – 6 = – 2 x  3y + 2x = 6
• 3y + 2x = 6 : x dan y  R
2
3

8. SOAL NO: 137
Grafik fungsi kuadrat terbuka kebawah jika :
A. f(x) = x² – 4 B. f(x) = 8 – 2x + x²
C. f(x) = 8 – 2x – x² D. f(x) = 2x² – 6x + 10
• PEMBAHASAN.
• Persamaan umum fungsi kuadrat :
• f(x) = ax² + bx + c
• Grafik fungsi kuadrat terbuka kebawah jika
nila koefisien x² adalah negatif ( a = – )
• Dari pilihan A,B,C dan yang memenuhi syarat
adalah f(x) = 8 – 2x – x² karena nilai a = – 1
• f(x) = 8 – 2x – x² .

9. SOAL NO: 138
Grafik f(x) : x² – x – 6 ; x  Real akan menghasilkan f(x) < 0 jika
daerah asal … A. {x / x < – 2 , xR} B. {x / x < – 2 , xR}
C. {x / – 2 > x > 3, xR} D. {x / – 2 < x < 3, xR}
• PEMBAHASAN.
• f(x) = x² – x – 6 memiliki grafik
seperti gambar di samping.
• Grafik terlukis menghasilkan f(x) < 0
• dengan daerah asal – 2 < x < 3
• { x / – 2 < x < 3 , x  R }.
– 2 3
– 6

10. SOAL NO: 139
Koordinat titik balik f(x) = 8 – 2x – x² adalah …
A. { – 3 , 5 } B. { – 2 , 10 } C. { – 1 , 9 } D. { 0 , 8 }
PEMBAHASAN.
f(x) = 8 – 2x – x² memiliki grafik dengan
sumbu simetri x= –(–2) / (–2) = –1.
Grafik f(x) = 8 – 2x – x² terlukis memiliki
titik puncak {–b / 2a , f(–b / 2a)}
Karena nilai –b / 2a = – 1 dan nilai f(–
1)=8 + 2 – 1 = 9 maka titik balik grafik =
{ –1 , 9 }
{ – 1 , 9 }.
– 4 – 1 2
X
Y
9

11. SOAL NO: 140
Koordinat titik balik f(x) = – x² + 6x + 16 adalah …
A. { 2 , 23 } B. { 3 , 25 } C. { 4 , 23 } D. { 4 , 25 }
PEMBAHASAN.
f(x) = – x² + 6x + 16 memiliki grafik
dengan sumbu simetri x= (–6) / (–2) = 3.
Grafik f(x) = – x² + 6x + 16 terlukis
memiliki titik puncak {–b / 2a , f(–b / 2a)}
Karena nilai –b / 2a = 3 dan nilai f(3)= –
(3)² + 6(3) + 16 = 25 maka titik balik
grafik = { 3 , 25 }
{ 3 , 25 }.
X
Y
25
–2 3 8

12. SEKIAN
Terima Kasih
Jangan Lupa Lanjutkan .
Kompetensi Berikutnya.
Seri Berikutnya..