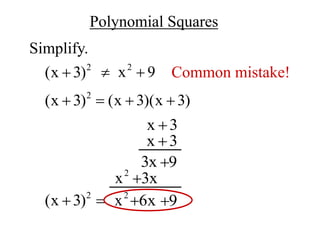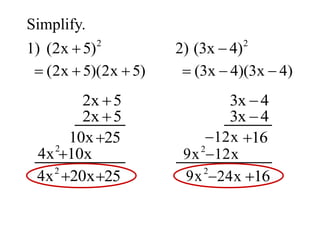The document provides instructions on multiplying polynomials and binomials using various methods. It explains how to multiply a polynomial by a monomial using the distributive property. It also describes how to multiply two binomials mentally using the FOIL method (First, Outer, Inner, Last), which results in a trinomial. Examples are provided to illustrate multiplying polynomials and binomials step-by-step.

1. Objective - To multiply polynomials.
Multiply the polynomial by the monomial.
1) 3(x + 4)
2)
3) 2
6k(2k 4k 3)
 
2a(a 5)

3x 12

2
2a 10a

3 2
12k 24k 18k
 
Distributive Property

2. Multiplying Polynomials
Horizontal Method
(x 5)(2x 3)
 
(x 5) 2x
  + (x 5) 3
  
2
2x 10x
 + 3x 15
 
2
2x 7x 15
 
Vertical Method
(x 5)(2x 3)
 
x 5

2x 3

15

3x

10x

2
2x
2
2x 7x
 15


3. Polynomial Squares
Simplify.
2
(x 3)
 2
x 9
  Common mistake!
2
(x 3)
 (x 3)(x 3)
  
x 3

x 3

9

3x
3x

2
x
2
x 6x
 9

2
(x 3)
 

4. Simplify.
1) 2)
2
(2x 5)

2x 5

2x 5

25

10x
10x

2
4x
2
4x 20x
 25

(2x 5)(2x 5)
  
2
(3x 4)

3x 4

3x 4

16

12x

12x

2
9x
2
9x 24x
 16

(3x 4)(3x 4)
  

5. 5x

Objective - To multiply binomials
mentally using FOIL.
Often the product
of two binomials = Trinomial
(x 3)(x 5)
  =
x 3

x 5

15

3x

2
x
2
x 2x
 15

Takes too long!
Quadratic
Term Linear
Term
Constant
Term
2
x 2x
 15


6. For use with the product of binomials only!
(x 3)(x 5)
 
First Outer Inner Last

7. For use with the product of binomials only!
(x 3)(x 5)
 
First Outer Inner Last

8. For use with the product of binomials only!
(x 3)(x 5)
 
First Outer Inner Last

9. For use with the product of binomials only!
(x 3)(x 5)
 
First Outer Inner Last

10. For use with the product of binomials only!
(x 3)(x 5)
 
First Outer Inner Last

11. For use with the product of binomials only!
(x 3)(x 5)
 
First Outer Inner Last
2
x

12. For use with the product of binomials only!
(x 3)(x 5)
 
First Outer Inner Last
2
x 5x


13. For use with the product of binomials only!
(x 3)(x 5)
 
First Outer Inner Last
2
x 5x
 3x


14. For use with the product of binomials only!
(x 3)(x 5)
 
First Outer Inner Last
2
x 5x
 3x
 15


15. For use with the product of binomials only!
(x 3)(x 5)
 
First Outer Inner Last
2
x 5x
 3x
 15

2
x 2x 15
 

16. Try...
(m 3)(m 6)
 
First Outer Inner Last
2
m 6m
 3m
 18

2
m 9m 18
 

17. Use FOIL to multiply the binomials below.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
(y 7)(y 4)
 
(m 2)(m 8)
 
(x 6)(x 4)
 
(t 10)(t 6)
 
(x 4)(x 5)
 
(x 3)(x 8)
 
(y 7)(y 9)
 
(x 2)(x 11)
 
(2 m)(7 m)
 
(6 k)(4 k)
 
2
y 11y 28
 
2
m 10m 16
 
2
x 2x 24
 
2
t 4t 60
 
2
x 9x 20
 
2
x 5x 24
 
2
y 16y 63
 
2
x 9x 22
 
2
14 5m m
 
2
24 10k k
 

18. Use FOIL to multiply the binomials below.
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
(2x 3)(x 6)
 
(k 5)(2k 7)
 
(m 6)(2m 5)
 
(3x 4)(x 7)
 
(2x 9)(x 6)
 
2 2
(x 9)(x 5)
 
2
(k 1)(6k 3)
 
(m 5)(m 5)
 
(4t 7)(4t 7)
 
(2x 3)(m 5)
 
2
2x 15x 18
 
2
2k 17k 35
 
2
2m 7m 30
 
2
3x 17x 28
 
2
2x 21x 54
 
4 2
x 4x 45
 
3 2
6k 3k 6k 3
  
2
m 25

2
16t 49

2mx 10x 3m 15
  