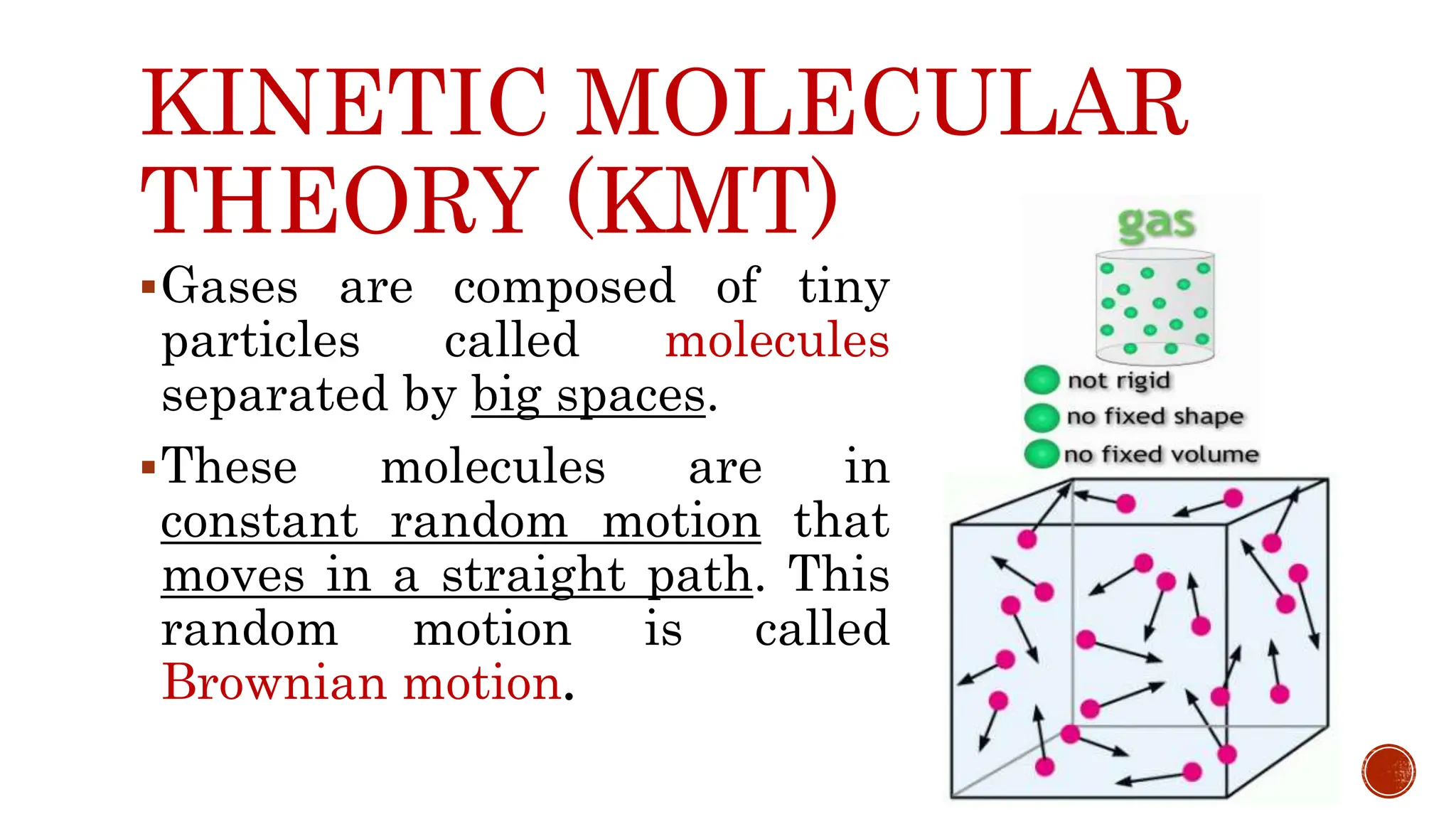
The kinetic molecular theory explains gas behavior through the motion of molecules, which occupy space, have mass, and display properties like pressure, temperature, and volume. Key gas laws including Boyle's Law, Charles' Law, and Gay-Lussac's Law describe the relationships between these properties, revealing how changes in one affect the others. The combined gas law incorporates pressure, volume, and temperature, highlighting its practical applications in everyday scenarios such as cloud formation and refrigeration.

2. KINETIC MOLECULAR
THEORY (KMT)
This model is used to describe the
behavior of gases.
It is used to explain properties of
gases, such as pressure,
temperature, and volume, in terms of
atoms.

3. KINETIC MOLECULAR
THEORY (KMT)
Gases are composed of tiny
particles called molecules
separated by big spaces.
These molecules are in
constant random motion that
moves in a straight path. This
random motion is called
Brownian motion.

4. KINETIC MOLECULAR
THEORY (KMT)
Due to movement, gas
molecules also hit the walls
of its container. The force
exerted on the wall is called
gas pressure.
Gases have masses, so they
are affected by gravity.

5. KINETIC MOLECULAR
THEORY (KMT)
The collision of gas molecules
is perfectly elastic. Thus,
energy is neither lost nor
gained.
Gas temperature is due to the
kinetic energy of the molecules.
More movement means higher
temperature and vice versa.

6. GASES
• Gas is a state
of matter that
has no fixed
shape and no
fixed volume.
• Gases have a
lower density
than other
states of
matter, such
as solids and
liquids.

7. THE PROPERTIES
OF GASES
Temperature
The temperature of a gas is the
measure of its hotness or coldness.
It is related to the average kinetic
energy of its molecules.
It can be measured in Celsius or Kelvin.
Kelvin is the absolute scale.

8. THE PROPERTIES
OF GASES
Mass
The amount of gas or its mass
could be expressed in moles
or grams.

9. THE PROPERTIES
OF GASES
Volume
The volume of a gas is the amount of
space occupied by the gases.
Gases have the tendency to occupy all
the spaces of the container that they
are confined.
The common units used in expressing
the volume of a gas are liter (L) and
milliliter (ml).

10. THE PROPERTIES
OF GASES
Pressure
The pressure of a confined gas
is the average effect of the
forces of the colliding
molecules.

11. INSTRUMENTS: INSTRUMEN
TS:
INSTRUMENTS:
VOLUME TEMPERATURE PRESSURE

12. 1 mL = 1 cm3
1 L = 1 dm3
1 m3 = 1000
L
1 L = 1000
mL
oF = 1.8 oC + 32
oC = (oF – 32)
0.56
K = oC + 273
1 atm = 760 mmHg
1 atm = 76 cmHg
1 atm = 760 torr
1 atm = 101325 Pa
1 atm = 14.6956 psi
VOLUME TEMPERATURE PRESSURE

20. VOLUME TEMPERATURE PRESSURE
is the
amount of
space
occupied
by a
matter
is the
degree of
hotness or
coldness
of a matter
is the
average
effect of the
forces of the
colliding
molecules

21. Robert Boyle
The pressure of a gas is
inversely proportional with
its volume.
“As the pressure increases,
the volume of a gas decreases
at constant temperature or
vice versa.”
BOYLE’S LAW

22. Wherein:
P1 = Initial Pressure (atm)
P2 = Final Pressure (atm)
V1 = Initial Volume (L)
V2 = Final Volume (L)
V1P1= V2P2
BOYLE’S LAW

23. BOYLE’S LAW
How much pressure is needed to change the volume of
a dry gas from 70 L to 10 L keeping the temperature
constant? The original pressure is 1 atm.
Given:
Required:
Equation:
Solution:
Answer:
70 L
10 L
1 atm
= V1
= V2
= P1
P2 = ?
70L(1 atm)
10 L
70 atm
V1 P1
V2
P2 =
P2 = =
10
P2 = 7

24. Oxygen gas inside a 1.5 L gas tank has a pressure of 0.95 atm.
Provided that the temperature remains constant, how much
pressure is needed to reduce its volume by ½.
Given:
Required:
Equation:
Solution:
Answer:
1.5 L
0.95
atm
= V1
= P1
= V2
P2 = ?
1.5 L(0.95 atm)
0.75 L
V1 P1
V2
P2 =
P2 =
P2 = 1.9 atm
BOYLE’S LAW
0.75 L

25. APPLICATION OF BOYLE’S LAW
When you squeeze the
balloon, you are increasing
the pressure which
decreases the volume.

26. As you push air into the
tire, the increasing
pressure reduces the
volume of the air molecules
by packing them together.
APPLICATION OF BOYLE’S LAW

27. CHARLES’ LAW
Jacques Charles
The volume of a gas is
directly proportional with
its temperature.
“As the temperature
increases, the volume of a gas
increases at constant pressure
or vice versa.”

28. Wherein:
T1 = Initial Temperature
(K)
T2 = Final Temperature
(K)
V1 = Initial Volume (L)
V = Final Volume (L)
APPLICATION OF CHARLES’ LAW
V1T2= V2T1

29. The volume of a gas sample at 273 K is 2 L. At
what temperature would the gas be to increase
its volume to 4 L?
Given:
Required:
Equation:
Solution:
Answer:
273 K
2 L
4 L
= T1
= V1
= V2
T2 = ?
4 L (273 K)
2 L
V2 T1
V1
T2 =
T2 =
T2 = 546 K
CHARLES’ LAW

30. At 215 K, the volume of chlorine gas is 250 L.
Compute for the resulting volume if the temperature
is adjusted to 318K provided that the pressure
remains the same.
Given:
Required:
Equation:
Solution:
Answer:
215 K
250 L
318 K
= T1
= V1
= T2
V2 = ?
250
L
(318 K)
215 K
V1 T2
T1
V2 =
V2 =
T2 = 369.77
CHARLES’ LAW

31. GAY-LUSSAC’S LAW
Joseph Louis Gay-Lussac
The pressure of a gas is
directly proportional with
its temperature at
constant volume.
“As the temperature
increases, the pressure of a
gas increases at constant
volume or vice versa.”

32. GAY-LUSSAC’S LAW
P1T2 P2T1
=
Wherein:
P1= Initial Pressure
T1= Initial Temperature
P2= Final Pressure
T2= Final Temperature

33. The pressure of a nitrogen gas inside a rigid tank is 1.5
atmosphere at 30°C. What will be the resulting pressure
if the tank is cooled to 0°C?
GAY-LUSSAC’S LAW
Given:
Required:
Equation:
Solution:
Answer:
1.5 atm = P1
= T1
= T2
P2 = ?
1.5
atm
(273 K)
303 K
P1 T2
T1
P2 =
P2 =
P2 = 1.35 atm
30 °C
0°C
+
273
303 K
+ 273
273 K

34. A certain light bulb containing argon has a pressure of 1.20
atm at 18°C. If it will be heated to 85°C at constant
volume, what will be the resulting pressure?
GAY-LUSSAC’S LAW
Given:
Required:
Equation:
Solution:
Answer:
1.20
atm
= P1
= T1
= T2
P2 = ?
1.20 atm
(358 K)
291 K
P1 T2
T1
P2 =
P2 =
P2 = 1.48 atm
18 °C
85°C
+
273
291 K
+ 273
358 K

35. APPLICATION OF GAY-LUSSAC’S LAW

36. • Firing a bullet
When gunpowder burns, it
creates a significant amount
of superheated gas. The high
pressure of the hot gas
behind the bullet forces it
out of the barrel of the gun.
APPLICATION OF GAY-LUSSAC’S LAW

37. Pressure and volume are inversely related
to each other, and are both directly related
to temperature. The combined gas law
shows how one property changes if the
other two changed.
COMBINED GAS LAW

38. Wherein:
P1 = Initial Pressure
(atm)
P2 = Final Pressure
(atm)
T1 = Initial
Temperature(K)
T2 = Final
P1V1T2= P2V2T
1
COMBINED GAS LAW

39. P1V1T2
=P2V2T
1
COMBINED GAS LAW

40. The volume of a gas at 300 K and 2 atm is 0.6 L.
What is the volume of the gas at 253 K and 1 atm?
COMBINED GAS LAW
Given:
Required:
Equation:
Solution:
Answer:
300 K
2 atm
0.6 L
253 K
1 atm
= T1
= P1
= V1
V2 = ?
2 atm(0.6 L )
1 atm
P1 V1T2
P2 T1
V2 =
V2 =
V2 = 1.01 L
= T2
= P2
(253 K )
(300 K)

41. Helium gas has a volume of 0.25 L at 0°C at 1.0 atm.
What will be the final pressure if the volume is reduced
to 0.10 L at 45°C?
COMBINED GAS LAW
Given:
Required:
Equation:
Solution:
Answer:
0.25 L
273 K
1.0 atm
0.10 L
318 K
= V1
= T1
= P1
P2 = ?
1.0 atm(0.25 L )
0.10
L
P1 V1T2
V2 T1
P2 =
P2 =
P2 = 2.91
= V2
= T2
(318 K )
(273 K)

42. APPLICATIONS OF COMBINED GAS LAW
In lifestyle, the combined gas
law has applications. When
the quantity of gas remains
constant, but the pressure,
volume, and temperature
fluctuate, this rule
applies. Cloud formation,
refrigerators, and air
conditioners, for instance, are