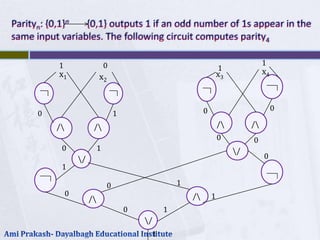
Circuit complexity is a model for computation that uses Boolean circuits to simulate functions. A Boolean circuit is a collection of gates like AND, OR, and NOT connected by wires without cycles. Circuit families can represent languages by having a circuit for each string length. The size and depth complexity of a circuit family is the minimum size and depth needed among equivalent circuits. The circuit satisfiability problem (CIRCUIT-SAT) of determining if a circuit outputs 1 for some input assignment is NP-complete, showing that circuit simulation is a hard problem.

1. •••••••••••••••••••••
Circuit Complexity
Ami Prakash
M.Sc. (CS)

2.  Simulate theoretical models such as Turing
machines.
 Provide a convinient computational model
for attacking the P versus NP related
questions.
 Provide an alternative proof of the Cook-
Levin Theorem that SAT is NP-complete.

3. Definition
 A Boolean circuit is a collection of gates and
inputs connected by wires.
 Cycles ain’t permitted.
 Gates take three forms :
/ /
OR gate NOT gate
AND gate

4.  To a boolean circuit C with n input variables, we
associate a function fc:{0,1}n {0,1},
where if C outputs b when its inputs x1,….,xn are
set to a1,…,an we write
fc(a1,…,an)=b
 A function with k output bits computes a
function whose range is {0,1}k

5. 1 0 1
1 x4
x1 x2 x3
0 0
0 1
/ / / /
0 0
0 1 /
/ 0
1
0 1
0 / 1
/
0 1
/
1

6.  Why family of circuits?
 Any particular circuit can handle only inputs of some
fixed length, whereas a language may contain strings of
different lengths.
 Hence to test language membership we use an entire family
of circuits.

7. Definition
 A Circuit Family C is an infinite list of
circuits, (C0,C1,C2,….), where Cn has n input
variables.
 We say that C decides a language A over {0,1}
if, for every string w,
w ∈ A iff Cn(w)=1
where n is the length of w.

8.  The size of a circuit is the number of gates that
it contains.
 Two circuits are equivalent if they have the
same input variables and output the same value
on every input assignment.
 A circuit is size minimal if no smaller circuit is
equivalent to it.

9.  A circuit family for a language is size minimal if
every Ci on the list is a minimal circuit.
 The size complexity of a circuit family
(C0, C1, C2, …) is the function f :N N,
where f(n) is the size of Cn.
 The depth of a circuit is the length of the
longest path from an input variable to the
output gate.

10.  The circuit size complexity of a language is the
size complexity of a minimal circuit family for
that language or it is the minimal size of any
circuit computing Boolean function f.
 Similarly circuit depth complexity of a
Boolean function f is the minimal depth of any
circuit computing f.

11.  The circuit complexity of a language is related to
its time complexity. Any language with small
time complexity also has a small circuit
complexity.
 Statement of the theorem:
Let t: N N be a function, where t(n)≥n.
If A ∈ TIME(t(n)), then A has circuit complexity
O(t2(n)).

12.  A Boolean circuit is satisfiable if some setting
of the inputs causes the circuit to output 1.
 The circuit-satisfiablity problem tests whether
a circuit is satisfiable.
CIRCUIT-SAT={<C>| C is a satisfiable Boolean
circuit}

13.  Statement: CIRCUIT-SAT is NP-complete.
 Definition: NP-complete.
 A language B is NP complete if it is in NP and every language A ∈ NP is
polynomial time reducible to B.
 Approach:
 Show that CIRCUIT-SAT is in NP.
 Any language A in NP is polynomial time reducible to
CIRCUIT-SAT.

14.  The first is obvious.
 To the second we must give a polynomial time reduction f that maps
strings to circuits, where
f(w)=<C>
implies that w ∈ A iff Boolean Circuit is satisfiable.
 Because A is in NP, it has a polynomial time verifier V whose input has
the form <x,c>, where c is the certificate showing that x maybe in A.
 To construct f, we obtain the circuit simulating V using the method in
Theorem 1. We fill in the circuits that correspond to x with the
symbols of w. The only remaining inputs to the circuit correspond to
the certificate c. We call this certificate C and output it.
 If C is satisfiable, a certificate exists, so w is in A. Conversely, if w is in
A, a certificate exists, so C is satisfiable.

15.  To show that this reduction runs in polynomial
time:
 The running time of the verifier is nk for some k, so
the size of the circuit constructed is O(n2k)( by
Theorem1).
 Hence the running time of the reduction is O(n2k).

16.  Theory of Computation by Michael Sipser

17. •••••••••••••••••••••
Thank you!