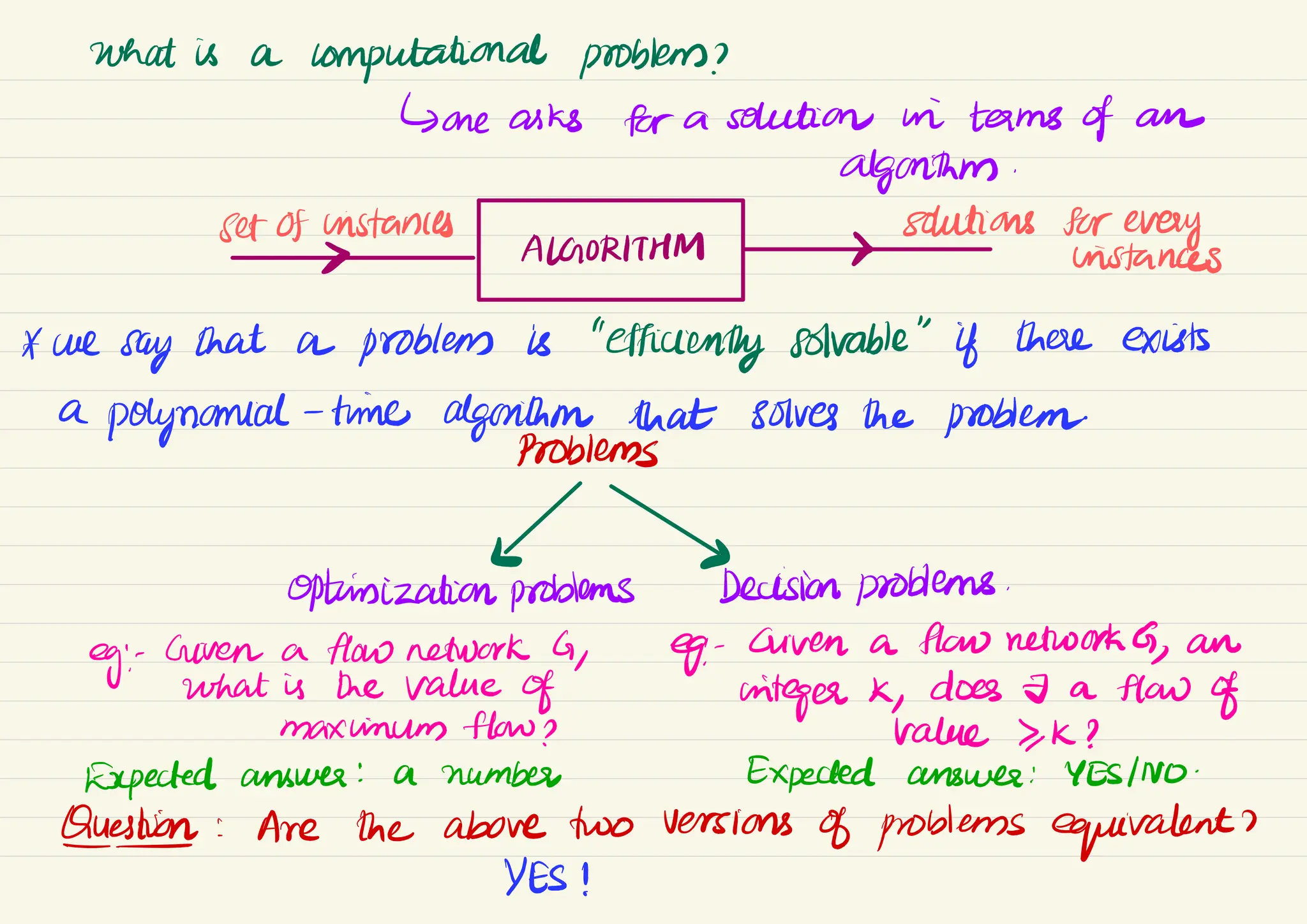
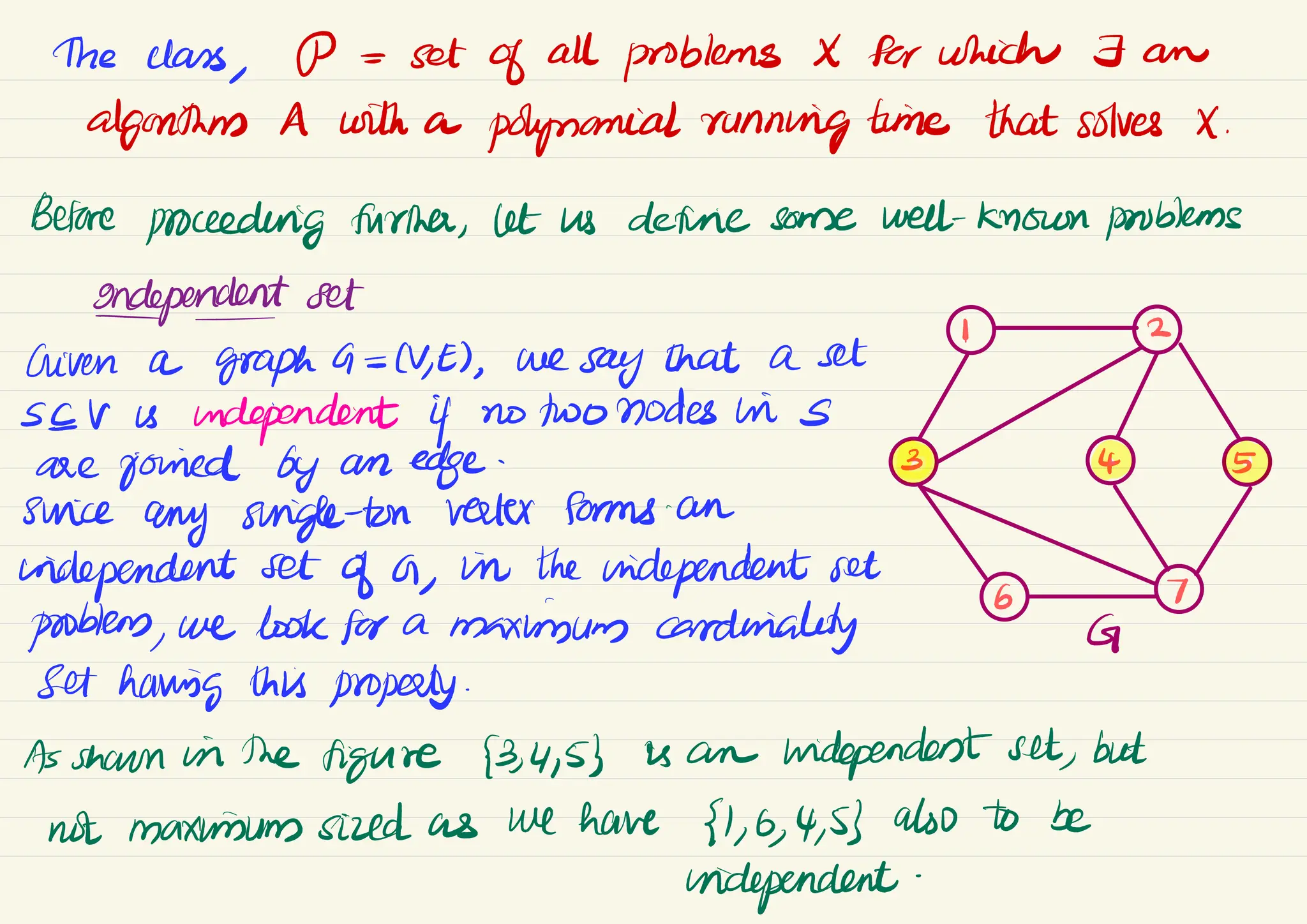
The document discusses computational problems, specifically differentiating between decision and optimization problems, and how they can be interconverted through polynomial-time algorithms. It explains the concepts of independent sets and vertex covers in graph theory, highlighting their equivalency in terms of difficulty. The document also touches on satisfiability problems and the significance of efficient certifiers, ultimately questioning whether P equals NP and exploring the hardest problems within NP.

1. Nand
computational intractability

2. what is a
computational problem?
↳one asks for a solution in terms of an
algorithme .
set of instances solutions for every
> ALGORITHM > instances
A we
say that a problem is "efficiently solvable" if there exists
a
polynomial-time algorithm that solves the problem
Problems
L S
optimization problems Decision problems.
egi
- Given a flow network G, eg: -Given a flow network
,
an
what is the value of integer K
,
does - a flow of
maximum flow ? value 2
,
K ?
Expected answer : a number Expected answer : YESINO-
Question : Are the above two versions of problems equivalents
YES !

3. Prooffortheequivalence
-
clearly,
if one can solve an optimization problem (in polynomial
time) ,
then one can answer the decision version of the same
problems in polynomial time ·
Her eg : suppose you know value of
max-flow =1
,
then to solve the decision version ,
its enough to check whether
KIl or not
conversely, by doing a briary search on the bound K
,
one
can transform a
polynomial-time answer to the decision
version of the problem to an answer to the optimization
version of the same
problem in polynomial time.
eg!-
Suppose you know how to solve the decision version of flaw in poly-time.
Now,
to solve the optimization version from this
,
we do the following
.
As max flaw value 11 = C
,
do a binary search -
ie, first run
(
eoutofs
the decision version also for K= C
. If Answer is YES, return 1 = c
,
else
update K
=
and run the
algo again
.
If answer is YES
,
then leCE,
C) ele le11, 2),and som .... By running the decision
also for flow log times , ' we can solve the optimistication version of flow.

4. thus,
the two versions are equivalent and we focus on decision versions,
morder to define thecomplexity classes
.
Formally,
an input to the computational problem will be encoded
as a finite
binary string s .
Let
Isl =
length of the strings .
A decision problem X can be identified with the set of strings
on which the answer is "YES".
An algorithms A for a decision problem receives an input
stungs and returns the values "YES" Or "NO"
Let Als) dendes the value returned by
A for the Input strings .
we
say that A solves the problem X
if for all string s
,
we have
Als) =
YES If SEX
.
Further
, A has a
polynomial running time if there is a
polynomial function PC) so
that inputs , the algorithm
taminates in OIPISD) steps.

5. the class
,
O = set
of all problems X for which I an
algorithms A with a
poliponial running time that solves X
.
Before proceeding further, let us define same well-known problems
dependent set
Il 2
Given a graph G = (V
,
E),
we
say that a set
SCV is
independent if no two nodes his
are joined by an edge. 3 4 5
swice
any single-ton vertex farmsan
independent set
of G,
in the independent set
6 7
problem,
we look for a maximum cardinality G
set having this property
.
As shar in the figure[3
, 4, 5) is an widependent set,
but
not maximum sized as we have $1,
6
,
4,53 also to be
independent

6. esteveLG = N, E),
we say that a set SEV is a
Vertex cover
of G
, if every edge eEE has atleast are point
his.
swice the vertex set V itself forms a I 2
Velez cover ,
in the Vertex cover problem,
we look for a minimums radicality 3 4 5
Vester cover
.
As shar in the figure, [1,
2
,
6
, 73 is a 6 7
G
raten cover of G
,
but it is not minimum as
,
52,
3, 73 is also a retex cover of G
.

7. Decision versions of the independent set problems and the
verter cover problem is as defined below
.
INDEPENDENT
SET
Input : a
graph G ,
and a the integer K
.
Question: Does a contains a independent set of size >K.
HERTEXCOVEh G ,
and a the integer K.
Question: Does a contains a Vertex cover of size <K.
We don't know how to solve either INDEPENDENT SET Or
VERTEX LOVER .
But
, we can establish that both the problems
are equivalently hard,
due to the
following result
.

8. lensal.
Let G = N
, E) be a
graph.
Then s is an
independent
set
if and only if V-S is a vetex cover.
S
prof
:
suppose that s is an kidpt set
.
& 0 o
consider any arbitrary edge e=
(u,v) in G
.
swices is midpt ,
both u and v cannot ① · 00
belong to s > either LEVIS or verls
V-
S
=> S is a vertex
cover of G
conversely,
-
Suppose that V-S is a vertex cover of G
.
consider
any
two modes u,
Ves .
Of UVEE(a), then
the ede ur does not have
any end etinv-s,
a contradiction to
the fact that s is a netex cover -
> uVKECG) =S is an indpt
-
setof G
-

9. Coronary : G has an independent set of size >K if and
only if G has a verter cover
of size N-K.
the
satisfability/
problems
suppose we are
given a set X
of
a boolean variables
CFALSE) GRUES
14
, -- -
ew ;
each takes values 0 or 1 :
An anignment for X is a function f:X - 50, 13-
By a term/literal over X ,
we mean
ei or ste
note that di = 1
(f I = 0
.
A clause is
smiply a disjunction of terms tivtzV . . . Uty
,
where tre [x,-Un, , ,
- -
an
eg: 1, Vevevey is a clause

10. A conjuctive normal form (CNF) is a
conjuction of clauses.
GNEM . . .
ACm where each C is a cause.
eg: -
(, ve2) & [Vv) N y)
A CNF formula E is said to be satisfiable If the z an
asignment v :
X-20, 13 st .
F evaluates to
be
eg: -let F= (, VM2) &VRV) & Luy) True.
Then 2 = 0
,
x= 2
, x3 = 0
My= 1 is a
satisfying assignment
of F-
let F =
(x, ve) avct) (, vi) a (T Vez)
has no
satisfying assignment
.

11. satisfiability-SAT) problem
-
Input : A CNF formula F YES F is satisfiable
No =
> F is unsatisfiable
Question : Is F satisfiable ?
Umatisfiability
(UNSAT)
Input : A CNF formula F YES
= F is satisfiable
Question : Is F unsatisfiable ? No > F is satisfiable.

12. Solving Is verifying:
verifying a solution to the problem is a simpler thing to do
than
actually solving it
.
B is an efficient certifies for a problem X If the
following
properties hold:
* B is a
polynomial-time algorithm that takes two arguments
sChistance of X) and + (a certificate)
&
* B outputs either YES or NO
A there is a
polynomial pin) st . strings ,
seX #) - a
string t of length <P(ISI) such that
B(s
,
t) =
YES
B can be
thought of as an algorithm that can decide whether an
instance s is YES , if it is
given some "help" in the form of a
"short" certificate

13. Examples & Efficient
certifiers
① An efficient certifies for the Independent set problem
,
In instances : G
certificate + : a
string corr to a set SEVIG) with 1517K
-
Califier B: for any pair UNES,
check .
Whether UVEECG) ?
output B(S
, t) =
YES
) the sets in an independent set
.
let X be the YES histances of the independent set problem.
then, GEX#) J an independent set SEV(G) with 1SK
/K
-
E) the string t corresponding to the set s is st .
Bla,
t)=
YES
swice It <N =
P(IVC)),
Bis are efficient certifies for
the problem.
-

14. (2) Another efficient certifice for the Independent set problem
,
In instances : G
cusing vertex cover
certificate + : a
string corr to a set S[VIG) with Islen-k
-
Califier B: check whether for each e=
/,
V) EE(G),
either
uts or Vess
output B(S
, t) =
YES
) the sets is a veetex cover
let X be the YES histances of the independent set problem-
then, GEX#) J an independent set SEV(G) with 1SK
/K
-
(by lemma
#) V-S is a verter cover
of h ,
and IV-s/n-k
E) the string + corresponding to theset V-S is st ·
B(a,
t)=
YES
swice It < n- 1 =
P(IVC)),
Bis are efficient certifies for
the problem.
-

15. (3) An efficient certifies for the SAT problem-
Instances : a CNF Formula #
certificate : a
string corr to an assignment of variables in F
-
Califier B: check whether the string evaluates to be true
-
output B(St) =
YES
) String evaluates to be true
.
let X be the YES histances of the SAT problem
then, FEX) J a
satisfying angement for F
# the
string t low to the the
satisfying
anignment evaluates to be true
=> B(AE) =
YES
Swice (t =
#variables in F, B is an efficient certifies for
-
the
sA
T problem
-

16. Quan:
why t[P(IS) condition in the efficient
certifies definition is important ?
consider the UNSAT problem.
let X be the YES instances of the UNSAT problem.
then an Input instance,
# which is a boolean CNF on say
,
in
variables
i St.
FEX #S # has no satisfying abigument
= each of the 2" possible assignment evaluates
to be false.
But wades to verify the above condition, possibly we need a
certificate t,
that can encode 2"possible assignments
,
in
which case t & P(IF) need not be true.
consequently,
we don't know whether the UNSAT problems has
an efficient certifies !

17. stands for "Non-determistic" polynomial time
-
the clas
,
NP =
set of all problems for which there
exists an
efficient certifies
.
It can be seen that PCNP-
NP
Prof: Let XEP; This implies
P
7 a
poly-time also A that solves X
to
prove XtNP ,
we need to p.
TJ
an efficient certifies B for X
.
we can design the certifies (algorithm) B as follows.
presented with an input Pari (S
,t),
B simply returns value A(S)
clearly B runs in
poly-time (as A does so)
Now, for a
string seX, At of length atmost plis),
we have
B(s
,
t) = YES ·
Now
if SeX ,
At of length almost PlsI) we
have B(SE) = No ·
(in SEX F a
string t of length atmost P(Is)
St.
BISt) =
YES =
) Bis an efficient certifie for X = XENO
-

18. Question
! Does 7 a
problem hiND that cannot be solved in
&
polynomial time p
ic, Is P*NP ?
#
a fundamental question in
algorithms,
whose solution will
you a 1 million dollars !!!
As PENP is two
good to be true, people believe that OENP-
In the absence
of progress in the above
questions, people
started
looking at a related but more approachable question
Question : What are the hardest problems in NP?
-
the most natural
way
to decide a "hardest" problem,
XENP
would be to see whether X is atleast as hard as
any
what does this mean? problem in NP!!