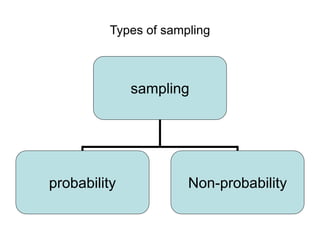
1) Sampling involves collecting data from a subset of individuals (the sample) rather than from the entire population. 2) There are two main types of sampling: probability sampling, where each individual has a known chance of being selected, and non-probability sampling, where the probability of selection is unknown. 3) Common probability sampling methods include simple random sampling, stratified sampling, systematic sampling, and cluster sampling. Non-probability methods include quota sampling and snowball sampling.

1. Sampling
Sampling

2. Some definitions
Population The group of people, items or units
under investigation.
Census Obtained by collecting information about
each member of a population.
Sample Obtained by collecting information only
about some members of a "population"
Sampling Frame The list of people from which the
sample is taken.It should be comprehensive,
complete and up-to-date.
Examples of sampling frame: Electoral Register;
Postcode Address File; telephone book.

3. POPULATION
Population:
In a statistical investigation the interest usually lies in the
assessment of the general magnitude and study of
variation w.r.to one or more characteristics relating to
individuals belonging to a group. This group of
individuals under study is known as Population or
Universe .
Example Of Population:
Total number of students studying in a school or college.

4. Finite population and infinite population:
A population is said to be finite
if it consists of finite number of units.
Example for Finite population.
Numbers of workers in a factory, production of articles in
a particular day for a company
The total number of units in a population is called
population size.
A population is said to be infinite if it has infinite number
of units.
Example for infinite population
The number of stars in the sky, the number of people
seeing the T.V programmes etc.

5. Parameter
Any population constant is called a parameter (or)
measure of the population is called parameter act of
various parameters mean() and variance 2 are
largely used besides correlation co-efficient,
regression co-efficient etc.

6. Statistic
A statistic is a function of observable random
variables and does not involve any unknown parameter.
Statistic is also a random variable mean x , variance s 2,
Student t =
n
s
x 

is a statistic.

7. Distinguish between complete enumeration
and sampling study
•In complete enumeration, each and every unit of the
population is studies and results are bond on all units
of the population
•Where a in sampling study only a selected number of
units are studied and results based on the data of these units.

8. Types of sampling
sampling
probability Non-probability

9. Probability Sampling
A probability sample is one in which each member
of the population has an equal chance of being selected.

10. Types of probability sample
There are five main types of probability sample.
The choice of these depends on nature of research problem,
the availability of a good sampling frame, money, time,
desired level of accuracy in the sample and data collection
methods •Simple random
•Systematic
•Random route
•Stratified
•Multi-stage cluster sampling

11. Non-Probability Sampling
In a non-probability sample,
some people have a greater, but unknown,
chance than others of selection .

12. Types of Nonprobability Sampling
•Quota sampling .
•Purposive sampling
•Snowball sampling
•Dimensional sampling

13. Difference between nonprobability and probability sampling
The difference between nonprobability and probability sampling
is that nonprobability sampling does not involve
random selection and probability sampling does.

14. Simple random sample
A simple random sample gives each member of the
Population an equal chance of being chosen.
e.g. give everyone on the Electoral register a number
Random numbers can be obtained using your calculator
a spreadsheet, printed tables of random numbers,
or by the more traditional methods of drawing
slips of paper from a hat, tossing coins or rolling dice.

15. Characteristics: (Simple random sample)
•Suitable where population is relatively small and where
sampling frame is complete and up-to-date
•Each person has same chance as any other of being selected
•Standard against which other methods are sometimes evaluated

16. Procedure: (Simple random sample)
•Select that many numbers from a table of random
numbers or using computer
•Obtain a complete sampling frame
•Give each case a unique number, starting at one
•Decide on the required sample size

17. Advantages
•ideal for statistical purposes

18. Disadvantages
•Expensive to conduct as those sampled may be
scattered over a wide area
•Hard to achieve in practice
•Requires an accurate list of the whole population

19. Sampling distributions

20. Example
• Take random sample of students.
• Ask “how many courses did you study for
this past weekend?”
• Calculate statistic, say, the sample mean.
Sample 1: 1 0 2 Mean = 1.0
Sample 2: 1 1 4 Mean = 2.0

21. Situation
• Different samples produce different
results.
• Value of a statistic, like mean or
proportion, depends on the particular
sample obtained.
• But some values may be more likely than
others.
• The probability distribution of a statistic
(“sampling distribution”) indicates the
likelihood of getting certain values.

22. Let’s investigate how sample
means vary….

23. Sampling distribution of mean
IF:
• data are normally distributed with mean
 and standard deviation , and
• random samples of size n are taken,
THEN:
The sampling distribution of the sample means is also
normally distributed.
The mean of all of the sample means is .
The standard deviation of the sample means
(“standard error of the mean”) is /sqrt(n).

24. Example
• Adult nose length is normally distributed
with mean 45 mm and standard deviation 6
mm.
• Take random samples of n = 4 adults.
• Then, sample means are normally
distributed with mean 45 mm and standard
error 3 mm [from 6/sqrt(4) = 6/2].

25. Using empirical rule...
• 68% of samples of n=4 adults will have an
average nose length between 42 and 48
mm.
• 95% of samples of n=4 adults will have an
average nose length between 39 and 51
mm.
• 99% of samples of n=4 adults will have an
average nose length between 36 and 54
mm.

26. What happens if we take larger
samples?
• Adult nose length is normally distributed
with mean 45 mm and standard deviation 6
mm.
• Take random samples of n = 36 adults.
• Then, sample means are normally
distributed with mean 45 mm and standard
error 1 mm [from 6/sqrt(36) = 6/6].