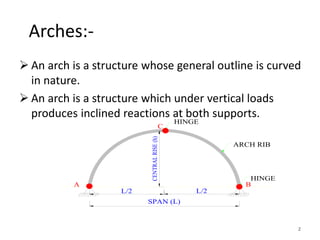
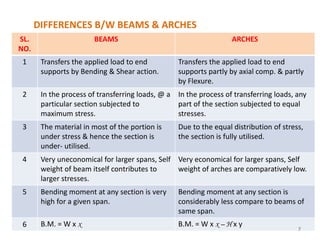
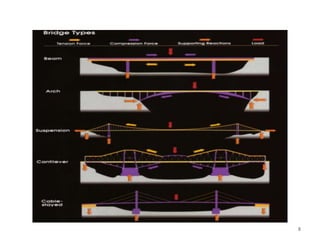
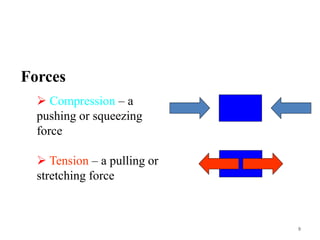
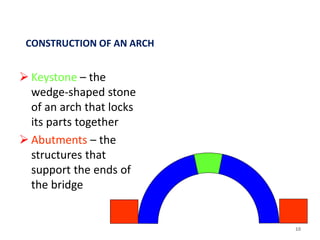
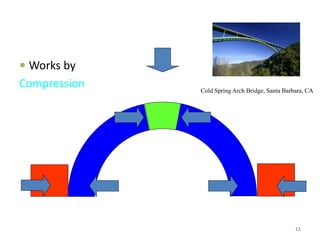
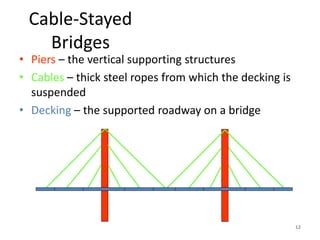
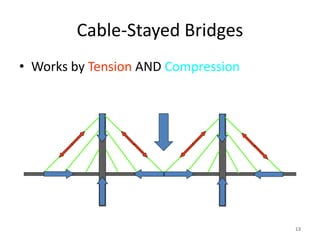
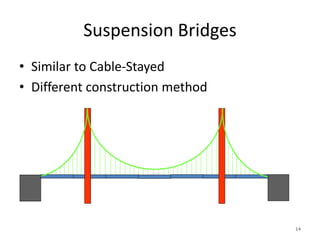
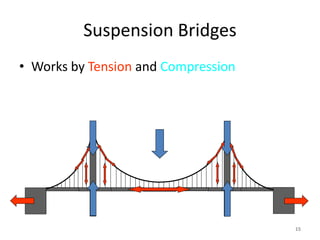
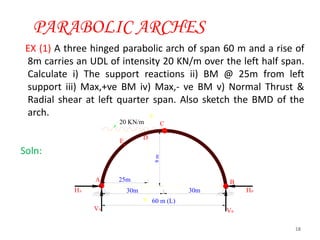
This document discusses three-hinged arches. It begins by defining an arch and its structural behavior under loads. It states that three-hinged arches are statically determinate, meaning horizontal displacement of the supports does not induce additional stresses. Arches can be classified based on material, shape, and structural behavior. The key forces on an arch are bending moment, normal thrust, and radial shear. Analysis of three-hinged arches involves calculating support reactions using equilibrium equations and determining bending moments and other forces. Parabolic arches have a circular profile defined by the radius and rise. Several examples are given of analyzing bending moments and other values for a given three-hinged parabolic arch.

1. THREE HINGED ARCHES
1
M.Arun Kumar
Assistant Professor
Kongu Engineering College,
Erode

2. Arches:-
 An arch is a structure whose general outline is curved
in nature.
 An arch is a structure which under vertical loads
produces inclined reactions at both supports.
2
CENTRAL
RISE
(h)
SPAN (L)
HINGE
HINGE
L/2 L/2
ARCH RIB
A B
C

3. We have 3-hinged, 2-hinged and fixed arches.
1-Three-hinged arches are statically determinate; hence,
horizontal displacement of the abutments does not produce
any additional stresses on the structural system.
2- Two-hinged arches and the fixed arches are statically
indeterminate; hence, displacement of the abutments
produces additional stresses in the structural system.
Furthermore, foundations of such arches should be on rock or
on very solid gravel.
3

4. CLASSIFICATION OF ARCHES:-
1. Based on Materials Used for Construction :-
Steel Arches
R.C.C. Arches
Masonry Arches etc…
2. Based on shape:-
Parabolic Arches
Circular or Segmental Arches
Elliptical Arches etc…
3. Based on structural behaviour:-
Three hinged arches
Two hinged arches
Fixed or Hinge less arches
Fixed arch with a hinge 4

5. CLASSIFICATION OF ARCHES:-
4. Based on structural behaviour:-
Open Arches
Solid Arches
FORCES AT ANY SECTION OF AN ARCH
Bending moment (M)
Normal Thrust (N)
Radial Shear (S)
5
L/4
A
HE
VE
S
N
tangent to arch


S
N
HA
VA
E

6. 6
Sl.
No.
STATICALLY DETERMINATE INDETERMINATE
(HYPERSTATIC)
1 Simply supported beam Continuous beam
2 Cantilever beam Propped cantilever beam
3 Three-hinged arch Fixed end arch
4 Three-hinged frame Rigid frame
EXAMPLES FOR STATICALLY DETERMINATE &
INDETERMINATE STRUCTURES

7. DIFFERENCES B/W BEAMS & ARCHES
SL.
NO.
BEAMS ARCHES
1 Transfers the applied load to end
supports by Bending & Shear action.
Transfers the applied load to end
supports partly by axial comp. & partly
by Flexure.
2 In the process of transferring loads, @ a
particular section subjected to
maximum stress.
In the process of transferring loads, any
part of the section subjected to equal
stresses.
3 The material in most of the portion is
under stress & hence the section is
under- utilised.
Due to the equal distribution of stress,
the section is fully utilised.
4 Very uneconomical for larger spans, Self
weight of beam itself contributes to
larger stresses.
Very economical for larger spans, Self
weight of arches are comparatively low.
5 Bending moment at any section is very
high for a given span.
Bending moment at any section is
considerably less compare to beams of
same span.
6 B.M. = W x x B.M. = W x x – H x y
7

8. 8

9. 9
Forces
 Compression – a
pushing or squeezing
force
 Tension – a pulling or
stretching force

10.  Keystone – the
wedge-shaped stone
of an arch that locks
its parts together
 Abutments – the
structures that
support the ends of
the bridge
10
CONSTRUCTION OF AN ARCH

11.  Works by
Compression
11
Cold Spring Arch Bridge, Santa Barbara, CA

12. Cable-Stayed
Bridges
• Piers – the vertical supporting structures
• Cables – thick steel ropes from which the decking is
suspended
• Decking – the supported roadway on a bridge
12

13. Cable-Stayed Bridges
• Works by Tension AND Compression
13

14. Suspension Bridges
• Similar to Cable-Stayed
• Different construction method
14

15. Suspension Bridges
• Works by Tension and Compression
15

16. ANALYSIS OF THREE HINGED ARCHES
STEPS:-
1) Draw the free body diagram including all the forces, dimensions
& reactions.
2) Calculate the support reactions using equilibrium conditions (i,e,
∑M=0, ∑V=0, ∑H=0).
i. ∑MA=0 ; Find the support reaction VB
ii. ∑V=0 ; Calculate the value of VA
iii. ∑MC=0 ; Calculate the value of HA
iv. ∑H=0 ; Calculate the value of HB
3) Find max. positive B.M ( i,e, Mx-x=VA x x – HA x y – w x x x x/2
i. 16
)
(
4
2
x
L
L
hx
y 


17. 0


dx
dM x
x
17
ii. Find value of “x’ by using condition
; x = ---------- m
iii. Substitute the value of ‘x’ in moment equation; calculate the value
of max. B.M.
4) Then use the same procedure to find – ve B.M
5) Normal thrust & Radial shear at any point of the arch is given by
Normal Thrust, N = V sin + H cos
Radial Shear, S = V cos + H sin
where ‘’ can be calculated as ;
6) Draw B.M.Diagram for the given arch.
)
2
(
4
tan
2
x
L
L
h
dx
dy


 

18. PARABOLIC ARCHES
18
EX (1) A three hinged parabolic arch of span 60 m and a rise of
8m carries an UDL of intensity 20 KN/m over the left half span.
Calculate i) The support reactions ii) BM @ 25m from left
support iii) Max,+ve BM iv) Max,- ve BM v) Normal Thrust &
Radial shear at left quarter span. Also sketch the BMD of the
arch.
Soln: 8
m
60 m (L)
30m 30m
A B
C
20 KN/m
25m
E
D
HB
VB
HA
VA
x
x

19. i. To find support reactions.
a) ∑MA = 0 ( +ve )
VB x 60 – 20 x 30 x 30/2 = 0
VB = 150 KN ( )
b) ∑V = 0 ( +ve)
VA + VB – 20 x 30 = 0
VA = 600 – 150 = 450 KN ( )
c) ∑MC = 0 ( +ve ) ∑H = 0 ( +ve)
19

20. 20
ii. To find B.M @ 25 m from left support,
Mx-x= VA x 25 – HA x yD – 20 X 25 x 25/2
(Rise) yD can be calculated as follows
yD =
iii. To find Max. + ve B.M.
iv. To find Max. - ve B.M.
)
(
4
2
x
L
L
hx

)
(
4
2
x
L
L
hx
y 

0


dx
dM x
x
)
(
4
2
x
L
L
hx
y 

0


dx
dM x
x

21. 21
v. To find Normal Thrust & Radial Shear:-
Normal Thrust, N = V sinq + H cosq
Radial Shear, S = V cosq + H sinq
vi. Draw B.M. Diagram.
Radius of circular arch is given by,
Arch profile at any point is given by,
CIRCULAR or SEGMENTAL ARCHES
4
)
2
(
2
L
h
h
R 

)
(
)
( 2
2
int
@
h
R
x
R
y anypo





22. 22
Cold Spring Arch Bridge, Santa Barbara, CA

23. 23
Marsh Rainbow Arch, Riverton, KS

24. 24
Pont du Gard, Nimes, France

25. Iron bridge, River Severn, England, built by Abraham Darby, 1779.
Members in compression; connections using dowels etc. 25

26. St Louis Rail Bridge, St Louis USA, Mississippi River. James Eades, 1874. First
true steel bridge. Three spans, each 152 m. 26

27. 27
THANK YOU