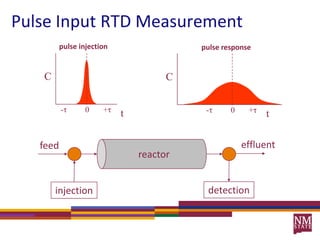
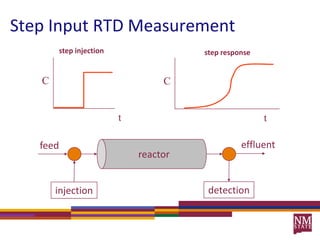
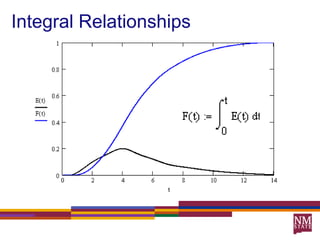
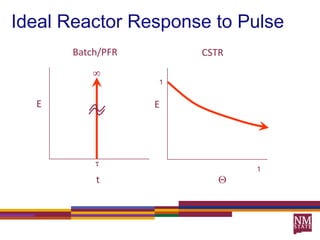
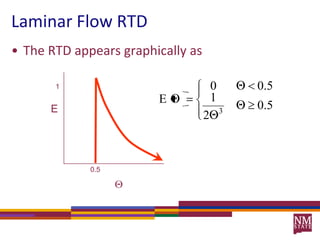
1) Residence time distributions (RTDs) are used to model imperfect mixing in chemical reactors and account for variations in flow patterns and residence times. 2) RTDs can be measured experimentally using inert tracers injected as pulses or steps and monitoring the effluent concentration over time. 3) The RTD function, E(t), represents the age distribution of molecules in the effluent and provides insights into the reactor's mixing behavior beyond the assumption of ideal reactors.

1. Ch E 441 - Chemical Kinetics and Reaction EngineeringResidence Time Distributionsin Chemical Reactors

2. Residence Time DistributionsThe assumption of a “perfectly mixed” reactor often falls short of reality.Residence time distributions are used to model the imperfect mixing behavior of real reactors.Cumulative age, F(t)External age, E(t)Internal age, I(t)

3. Residence Time DistributionsGas-liquid CSTR (A(g) + B(l) C(l))Reaction occurs at gas-liquid interfaceLiquid phase is perfectly mixedRate is proportional to bubble surface areaResidence time of gas bubble in reactor is proportional to bubble volumeLarger bubble escape rapidlySmaller bubbles may remain in reactor until consumedUnderstanding of RTDs is necessary for analysis

4. Residence Time DistributionsPBRSections of the catalyst bed may offer less resistance to flow, resulting in a preferred pathway through the bed.Molecules flowing through the “channel” do not spend as much time in the PBR as those taking another path.Consequently, there is a distribution of residence time for the PBR.

5. Residence Time DistributionsCSTRShort-circuiting may occur (the direct movement of material from inlet to outlet.Dead zones may exist (regions with a minimum of mixing and thus virtually no reaction takes place).

6. Residence Time DistributionsConcepts that must be addressed in approaching a solution to such problems:distribution of residence times occursquality of mixing varies with position in reactora model must used to describe the phenomenonAccounting for nonideality requiresknowledge of macromixing (RTD)application of the RTD to a reactor (micromixing) to predict reactor performance.

7. RTD FunctionsIn any reactor, the RTD can affect performanceIdeal Plug Flow and Batch ReactorsEvery atom leaving reactor is assumed to have resided in the reactor for exactly the same duration. No axial mixing.Ideal CSTRSome atoms leave almost immediately, others remain almost forever. Many leave after spending a period of time near the mean residence time. Perfect mixing.RTD is characteristic of mixing in a reactor.RTDs are not unique to reactor type. Different reactor types can have the same RTD.

8. Measurement of RTDRTD is measured experimentally by use of an inert tracer injected into the reactor at t = 0. Tracer concentration is measured at effluent as a function of time.Tracer must be non-reactive and non-absorbing on reactor walls/internals.Tracer is typically colored or radioactive to allow detection and quantification.Common methods of injection are pulse and step inputs.

9. Pulse Input RTD MeasurementAn amount of tracer No is suddenly (all at once) injected into the feed of a reactor vessel with flow at a steady state.Outlet concentration is measured as a function of time.reactoreffluentfeeddetectioninjection

10. Pulse Input RTD Measurementpulse injectionpulse responseCCreactor0-+0-+tteffluentfeeddetectioninjection

11. Pulse Input RTD MeasurementInjection pulse in system of single-input and single-output, where only flow (no dispersion) carries tracer material across system boundaries. The amount of tracer materialN leaving the reactor between t and t+t for a volumetric flowrate of iswhere t is sufficiently small that the concentration of tracer C(t) is essentially constant over the time interval.

12. Pulse Input RTD MeasurementDividing by total amount of tracer injected, No yields the fraction of material that has a residence time between t and t+t:where E(t) represents the residence-time distribution function.

13. Step Input RTD Measurementstep injectionstep responseCCreactortteffluentfeeddetectioninjection

14. Step Input RTD MeasurementIn general, the output concentration from a vessel is related to the input function by the convolution integral (Levenspiel):where the inlet concentration takes the form of either a perfect pulse input (Dirac delta function), imperfect pulse injection, or a step input.

15. Step Input RTD MeasurementConsidering a step input in tracer concentration for a system of constant :constant can be broughtoutside the integral

16. Divide by CoF(t)  fraction of molecules that have spent a time t or less in reactor (Cumulative age)Differentiate to obtain RTD function E(t)Step Input RTD Measurement

17. Step Input RTD MeasurementAdvantagesEasier to carry out experimentally than pulse testTotal amount tracer in feed need not be knownDisadvantagesOften difficult to maintain a constant tracer concentration in feed.differentiation of data, often leads to large error.Requires large amount of tracer, which in some cases can be expensive.

18. RTD CharacteristicsE(t) is sometimes called the exit-age distribution function. If the age of an atom is regarded as the amount of time it spends in the reactor, E(t) is the age distribution of the effluent.E(t) is the most often used distribution function for reactor analysis.

19. Fraction of exit stream that has resided in the reactor for a period of time shorter than a given value of t:Fraction of exit stream that has resided in the reactor for a period of time longer than a given value of t:Integral Relationships

20. Integral Relationships

21. Mean Residence TimeThe nominal holding time, , is equal to the mean residence time, tm.The mean value of the time is the first moment of the RTD function, E(t).can be used to determine reactor volume

22. 1st moment – mean residence time2nd moment – variance (extent of spread of the RTD)3rd moment – skewness (extent RTD is skewed relative to the mean)Other Moments of the RTD

23. Normalized RTD Function, E()A normalized RTD is often used to allow comparison of flow profiles inside reactors of different sizes, wherefor an ideal CSTR

24. Internal-Age Distribution, I()Fraction of material inside the reactor that has been inside for a period of time between  and +

25. RTD in a Batch or PFRSimplest caseSpike at t =  (or  = 1) of infinite height and zero width with an area of one

26. Effluent concentration is identical to that of reactor contents.A material balance for t > 0 on inert tracer injected as a pulse at t = 0RTD in a CSTR

27. RTD in a CSTRRecall definition of E(t), and substitute:

28. Ideal Reactor Response to PulseBatch/PFRCSTR1EE1t

29. Laminar Flow RTDVelocity profile in a pipe (cylindrical coordinates) is parabolic according to:Time for passage of an element of fluid is

30. The fraction of total fluid passing between r and r+dr is d/0:Laminar Flow RTD

31. Laminar Flow RTDCombining

32. Laminar Flow RTDThe minimum time the fluid will spend in the reactor isTherefore, the complete RTD function is

33. Laminar Flow RTDThe RTD appears graphically as1E0.5

34. RTD of PFR and CSTR in seriesCSTR (s) followed by PFR (p)CSTR output will be delayed by a time of p

35. RTD of PFR and CSTR in seriesPFR (p) followed by CSTR (s) PFR output will delayed the introduction of the pulse to the CSTR by a time of pRegardless of the order, the RTD is the same. However, the RTD is not a complete description of structure for a particular reactor or system of reactors (see Example 13-4).