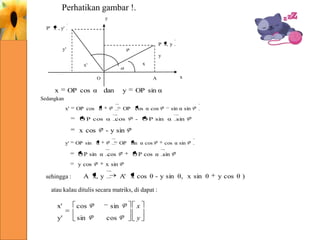
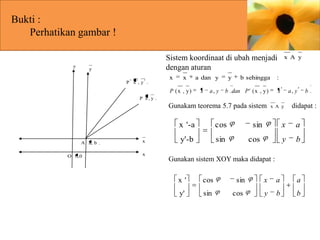
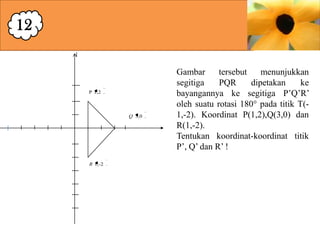
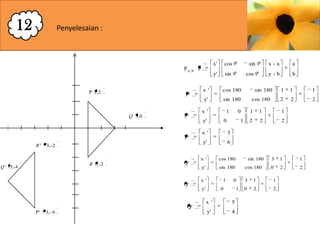
Dokumen ini membahas mengenai transformasi geometri khususnya rotasi, yang melibatkan pemutaran bangun geometri terhadap titik pusat tertentu dan memaparkan rumus serta contoh penerapan rotasi. Selain itu, disertakan berbagai contoh soal yang menunjukkan cara menemukan bayangan titik atau garis setelah mengalami rotasi dengan berbagai sudut. Penjelasan mengenai cara kerja transformasi ini menggunakan pendekatan geometris dan aljabar juga disertakan.

1. Presentasi Geometri Transformasi
Kelompok
3
Assalam’ualaikum. Wr.Wb
Peace be on you

2. “ROTASI”
Rotasi adalah proses memutar bangun geometri terhadap titik
tertentu yang dinamakan titik pusat rotasi dan ditentukan oleh arah rotasi
dan besar sudut rotasi.
Titik pusat rotasi adalah titik tetap atau titik pusat yang digunakan
sebagai acuan untuk menentukan arah dan besar sudut rotasi.
Arah rotasi disepakati dengan aturan sebagai berikut :
• Jika perputaran berlawanan dengan arah putar jarum jam, maka
rotasi ini bernilai positif (+).
• Jika perputaran searah jarum jam, maka rotasi ini bernilai negatif (-).

3. Rotasi merupakan transformasi karena :
Relasi dari v ke v
Fungsi
Injektif
Surjektif
Rotasi merupakan transformasi isometric karena tidak
mengubah jarak.

4. 1. Transformasi Rotasi dengan titik pusat di O(0,0)
Teorema 5.7
P 0,
x cos θ - y sin θ, x sin θ
P
y cos θ )
atau
P0,
P
x'
cos
sin
x
y'
sin
cos
y
untuk P x, y
v dan O 0,0
Bukti :
Misalkan
m
AOP
. karena
P0,
P
P ' , maka
m
POP'
dan m
AOP'

5. Perhatikan gambar !.
y
P' x' , y'
P x, y
y'
y
x
x'
O
x
OP cos α
x
A
dan
y
OP sin α
Sedangkan
x'
OP cos α
OP cos α cos
O P cos α cos
x cos
y'
OP sin α cos
O P sin α cos
sehingga :
- O P sin α sin
- y sin
OP sin α
y cos
O P cos α sin
A' x cos θ - y sin θ, x sin θ
atau kalau ditulis secara matriks, di dapat :
cos
y'
sin
cos α sin
x sin
A x, y
x'
sin α sin
sin
cos
x
y
y cos θ )

6. dari rumus diatas kita ambil contoh jika Rθ = R (O, θ ) diketahui R90ᶱ= R (O, 90ᶱ
)
maka kita subsitusikan :
A x, y
A x, y
A x, y
A x, y
A' x cos θ - y sin θ, x sin θ
A' x cos 90 - y sin 90 , x sin 90
A' x .0 - y. 1, x .1
A' - y , x )
y .0 )
y cos θ )
y cos 90 )

7. Dari penurunan rumus rotasi di atas. Suatu rotasi dengan
pusat O (0,0) dan sudut rotasi θ ditulis dengan R (O,θ) atau
Rθ, maka dapat dirumuskan ditabel dibawah ini.
Rotasi
Bayangan (x,y)
R90ᶱ= R (O, 90ᶱ
)
A x, y
R
R-90ᶱ= R (O, 90ᶱ
)
A x, y
R
90
R180ᶱ= R (O, 180ᶱ
)
A x, y
R
180
Rθ = R (O, θ )
A x, y
90
A'
Matriks
y, x
A' y,-x
A' - x,-y
A' x cos
- y sin
x sin
y cos
,

8. 2. Transformasi Rotasi dengan titik pusat di P(a,b)
Teorema 5.8
untuk setiap P x, y dan A a, b
v , maka
P'
,
P A,
x - a cos
- y - b sin
x
a sin
y
atau
P A,
P
x'
cos
sin
x -a
a
y'
sin
cos
y-b
b
b cos
b

9. Bukti :
Perhatikan gambar !
y
Sistem koordinaat di ubah menjadi
dengan aturan
y
P x ,y
x
x
P (x , y)
a dan y
x
a, y
y
x A y
b sehingga
:
b dan P' ( x , y )
x
a, y
b
P x, y
Gunakam teorema 5.7 pada sistem
x A y
didapat :
x '-a
A a, b
O 0,0
x
x
cos
sin
x
a
y'-b
sin
cos
y
b
Gunakan sistem XOY maka didapat :
x'
cos
sin
x
a
a
y'
sin
cos
y
b
b

10. Contoh Soal

11. 1.
Tentukan bayangan titik (5,2) oleh rotasi :
1. R90ᶱ
2. R-90ᶱ
3. R180ᶱ
Penyelesaian :
1.
5,2
R
90
A'
2.
5,2
R
90
A' 2,-5
3.
5,2
R
180
2,5
A' - 5,-2

12. - 2, 5
5,2
- 5,-2
2, - 5

13. 2.
Tentukan bayangan titik (-2,8) oleh rotasi R (O,135ᶱ !
)
Penyelesaian :
Jadi, bayangan adalah

14. 3.
Tentukan bayangan titik (5,-3) oleh rotasi R(P,90) dengan koordinat
titik P(-1,2) !
Penyelesaian :
Jadi, bayangannya adalah (4,8)

15. 4.
Tentukan bayangan garis y= 5x + 4 oleh rotasi R(O,-90) !
Penyelesaian:
x’ = y ↔ y = x’
y’ = -x ↔ x = -y’
Disubstitusikan ke y = 5x + 4
x’ = 5(-y’) + 4
↔ x’ = -5y’ +4
jadi, bayangannya adalah x = -5y +4

16. 5.
Tentukanlah bayangan P(3,-5) jika dirotasi 900 dengan pusat
rotasi di A(1,2)
Penyelesaian :
P(3, -5) = P(a, b)
A(1, 2) = A(x, y)
a’ = (a – x) cos a – (b – y) sin a + x
b’ = (a – x) sin a + (b – y) cos a + y
P a, b
R
A,
P' a' , b'
a’ = (3 – 1) cos 90o – (-5 – 2) sin 90o + 1 = 0 + 7 + 1 = 8
b’ = (3 – 1) sin 90o – (-5 – 2) cos 90o + 2 = 2 + 0 + 2 = 4
Jadi, bayangan P(3, 5) adalah P’(8, 4)

17. 6.
Persamaan bayangan garis x + y = 6 setelah dirotasikan pada pangkal
koordinat dengan sudut putaran +900 adalah . . .
Penyelesaian :
x'
-y maka y
-x'
y'
x maka x
y'
Substitusikan ke persamaan x + y = 6
x+y=6
y'
- x'
6 atau x'
y'
6
jadi bayangannya : x – y = -6

18. 7.
Persamaan bayangan garis 2x – y + 6 = 0 setelah dirotasikan pada pangkal koordinat dengan sudut
putaran -900 adalah . . .
x'
-y maka y
-x'
y'
x maka x
y'
Substitusikan ke persamaan 2x – y + 6 = 0
2x – y + 6 = 0
2 - y'
x'
6
0
x' 2 y'
6
0
jadi bayangannya : x + 2y– 6 = 0

19. 8.
Diberikan PO, 60° dan titik P (1,2). Tentukan koordinat P’= PO, 60° (P).
Penyelesaian :
θ
60, maka sin 60
P’= PO, 60° (1,2) =
1.
1
2
1
1
2
1
2.
2
2
3 , 1.
1
3 , 1
1
2
2
3
2.
1
2
3
2
1
1
1
2
2
Cara matriks :
P= PO, 60° (1,2) =
1
3 , cos 60
2
1
3
2
3
1
1
2
2
3 ,
1
2
3
1

20. 9.
Tentukan bayangan titik A ( -6, 2) jika dirotasikan dari titik pusat
sejauh 90°
Penyelesaian :
Dengan cara matriks :
x '
0
y'
1
x '
1
0
0
y'
2
y'
6
Cara bayangan (x,y)
A x, y
A - 6 ,2
R
R
90
90
A'
y, x
A'
2,- 6
0
y
1
1
0
6
2
1 2
6
x '
x
0
Maka A’ = ( -2, -6)

21. 10
Tentukan persamaan bayangan garis y = 5x + 2 jika dirotasikan dari pusat O sejauh 90°
Penyelesaian :
x '
0
y'
1
1
0
x '
y'
x
y
y
x
Atau y = -x’ dan x = y’ disubsitusikan ke pers y = 5x+2 sehingga menjadi :
y = 5x + 2
-x’ = 5 (y’) +2
-x’ – 5y’ = 2
x’ + 5y’ = -2
jadi persamaan bayangan garis adalah x + 5y = -2

22. 11
Diketahui sebuah garis dengan persamaan 2x + 5y = 12
Tentukan bayangan garis tersebut jika diputar dari titik pusat P(3,1)
sejauh 90°.
Penyelesaian :
Maka
x '
y'
y
x
1
3
x '-a
y'-b
1
1
0
x '
y'
1
0
y
x
3
4
2
x
3
y
1
x’ = -y + 4 → y = -x’ + 4 …………. (1)
y’ = x -2
→ x = y’ + 2 ……………(2)
persamaan (1) dan (2) di subtitusikan ke persamaan 2x + 5y = 12
sehingga :
2x + 5y = 12
2 (y’ + 2 ) + 5 (-x’ + 4 ) = 12
2y’ + 4 – 5x’ + 20 = 12
2y’ – 5x’ + 12 = 0
-5x’ +
2y’ = 12 x (-)
5x’ – 2y’ = 12
Jadi persamaan bayangan adalah 5x – 2y = 12

23. 12
P 1,2
Q 3,0
R 1,-2
Gambar
tersebut
menunjukkan
segitiga
PQR
dipetakan
ke
bayangannya ke segitiga P’Q’R’
oleh suatu rotasi 180° pada titik T(1,-2). Koordinat P(1,2),Q(3,0) dan
R(1,-2).
Tentukan koordinat-koordinat titik
P’, Q’ dan R’ !

24. 12
Penyelesaian :
P A,
x'
cos
y'
P
sin
sin
P'
Q 3,0
P'
x '
cos 180
sin 180
x '
1
y'
R ' - 3,-2
R 1,-2
Q ' - 5,-4
x '
Q'
P' - 3,- 6
1
2
2
2
1
1
1
2
2
2
6
x '
cos 180
sin 180
x '
1
y'
Q'
1
3
y'
Q'
1
cos 180
1
y'
P'
b
sin 180
0
0
a
y-b
cos
y'
P 1,2
x -a
sin 180
cos 180
0
0
1
x '
5
y'
4
3
1
1
0
2
2
3
1
1
0
2
2

25. R'
x '
cos 180
y'
R'
sin 180
x '
y'
1
0
x '
1
cos 180
0
1
1
2
2
1
1
1
2
2
1
2
2
3
y'
R'
sin 180
2
Jadi segitiga P’Q’R’ titik koordinatnya P(-3,-6),Q(-5,-4) dan R(-3,-2).

26. Terima Kasih
Wassalamualaikum.Wr.wb