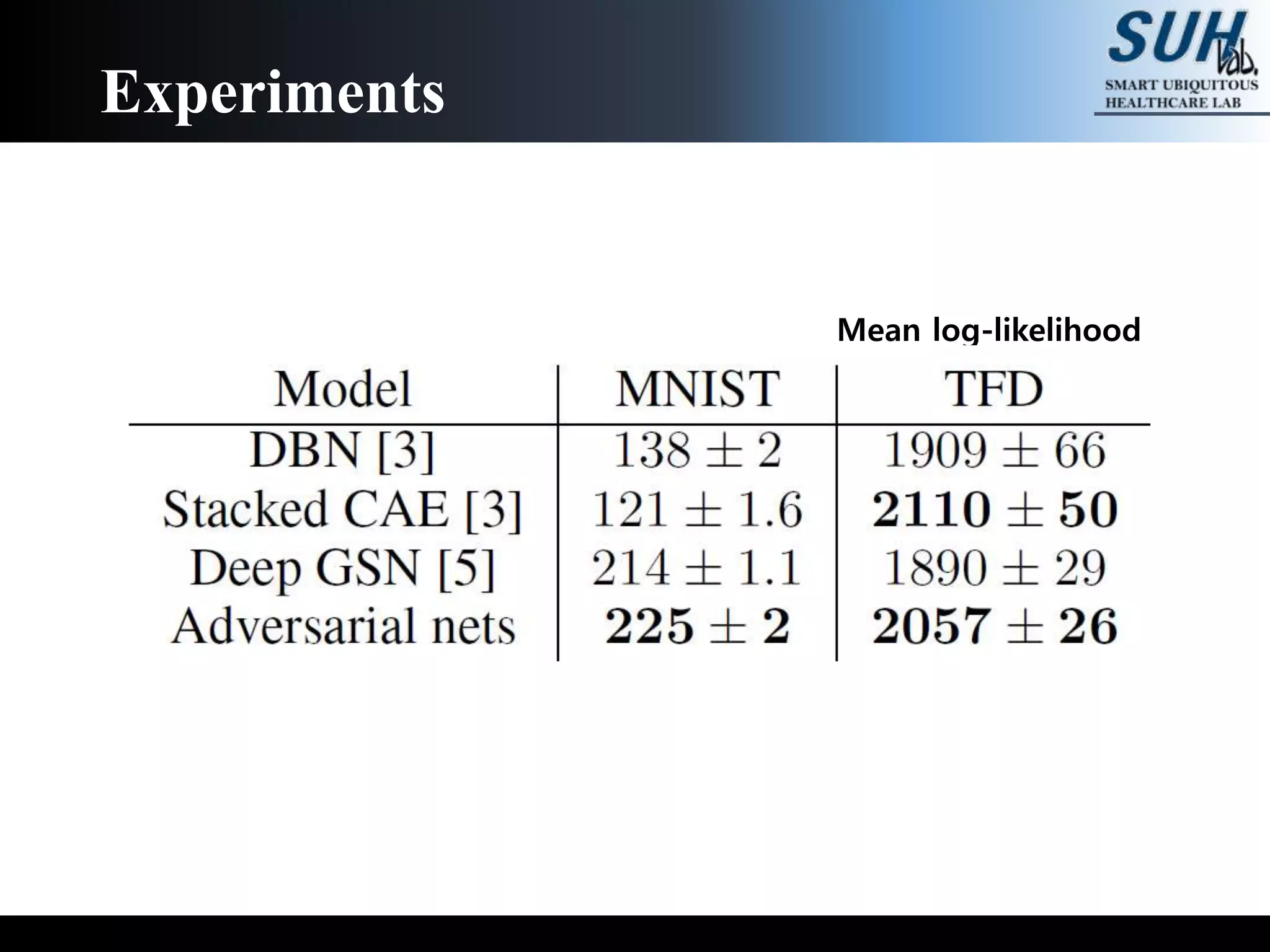
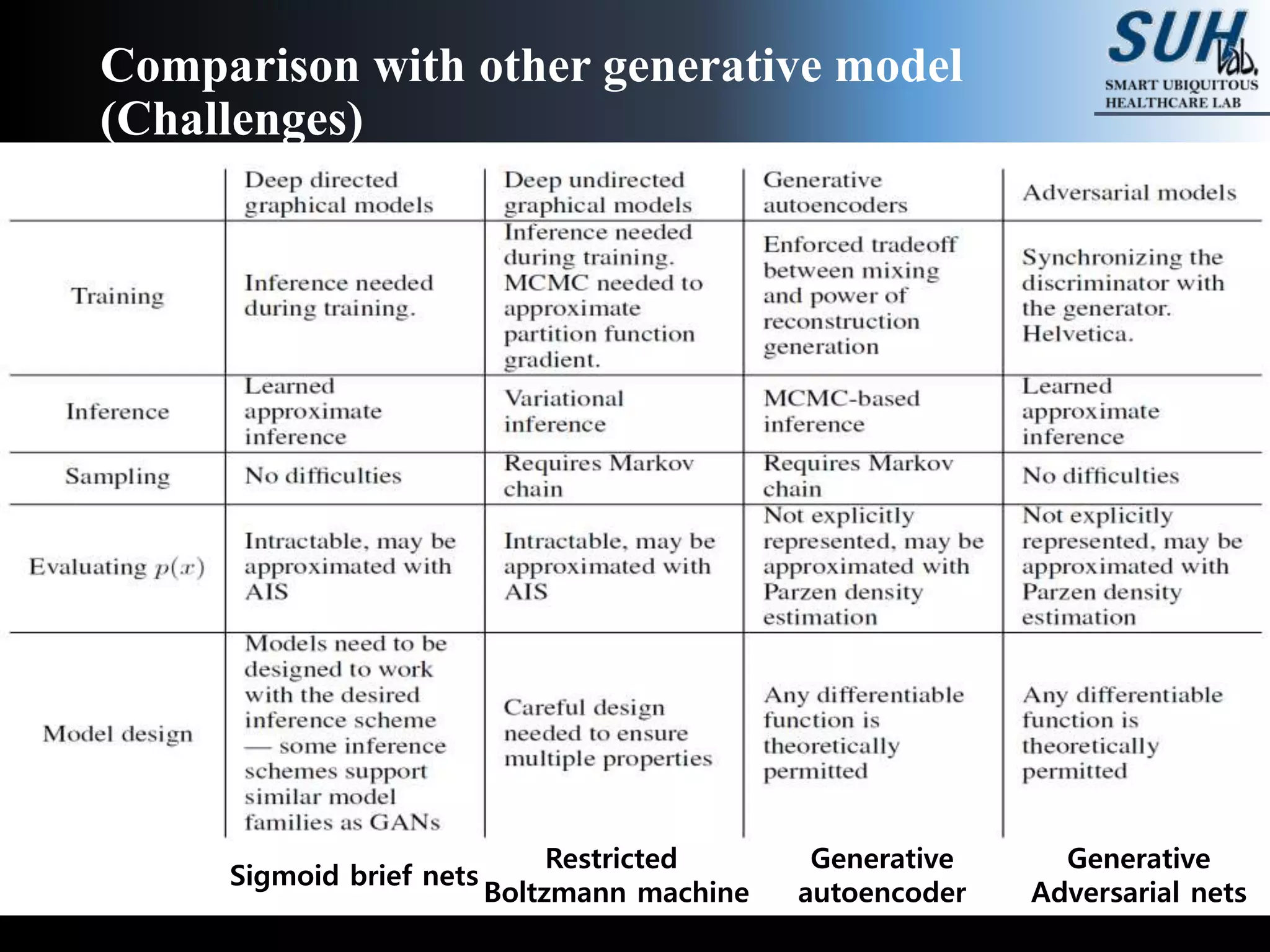
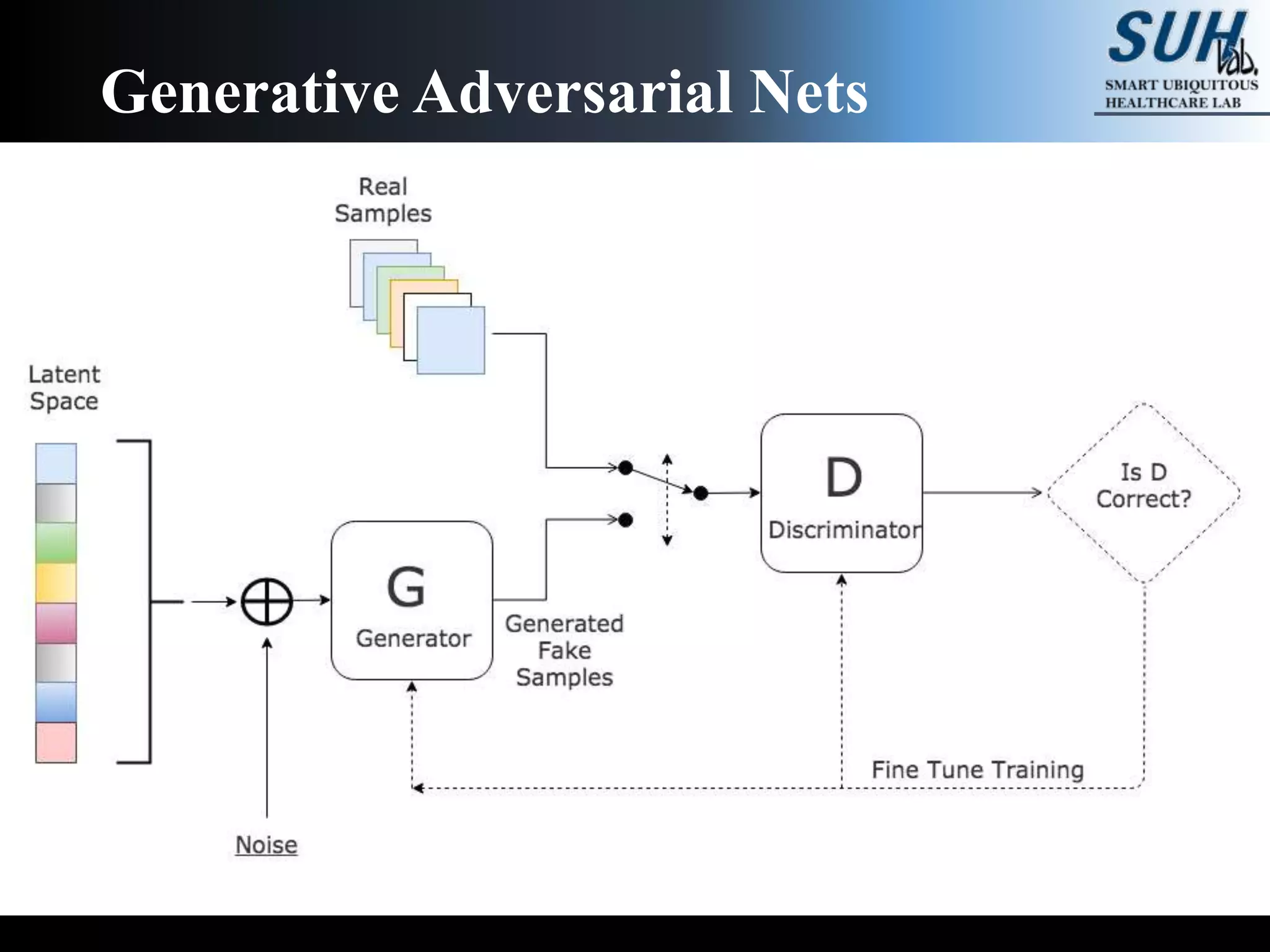
This document discusses generative adversarial networks (GANs). GANs are a class of machine learning frameworks where two neural networks, a generator and discriminator, compete against each other. The generator learns to generate new data with the same statistics as the training set to fool the discriminator, while the discriminator learns to better distinguish real samples from generated samples. When trained, GANs can generate highly realistic synthetic images, videos, text, and more. The document reviews several papers that apply GANs to image transformation, super-resolution image generation, and generating images from semantic maps. It also explains how GANs are trained through an adversarial game that converges when the generator learns the true data distribution.





![Learning of Adversarial nets
Learn generator’s distribution 𝒑 𝒈 over data x
Input noise
variable
𝒑 𝒛(𝒛)
Data
𝒙
Mapping to
data space
𝑮(𝒛; 𝜽 𝒈)
Discriminator
𝑫(𝒙; 𝜽 𝒅) Probability
that x came
from the
(real) data
𝑫(𝒙)
Train G to Minimize 𝐥𝐨𝐠(𝟏 − 𝑫 𝑮 𝒛 )
min
𝐺
max
𝐷
𝑽(𝑫, 𝑮)
= 𝔼 𝒙~𝒑 𝒅𝒂𝒕𝒂(𝒙) 𝒍𝒐𝒈 𝑫 𝒙 + 𝔼 𝒛~𝒑 𝒛(𝒛)[𝒍𝒐𝒈 𝟏 − 𝑫 𝑮 𝒛 ]
Train D to maximize the probability of assign correct label to
both training sample and samples from G (generated sample)](https://image.slidesharecdn.com/reviewofgenerativeadversarialnets-190711044929/75/Review-of-generative-adversarial-nets-8-2048.jpg)
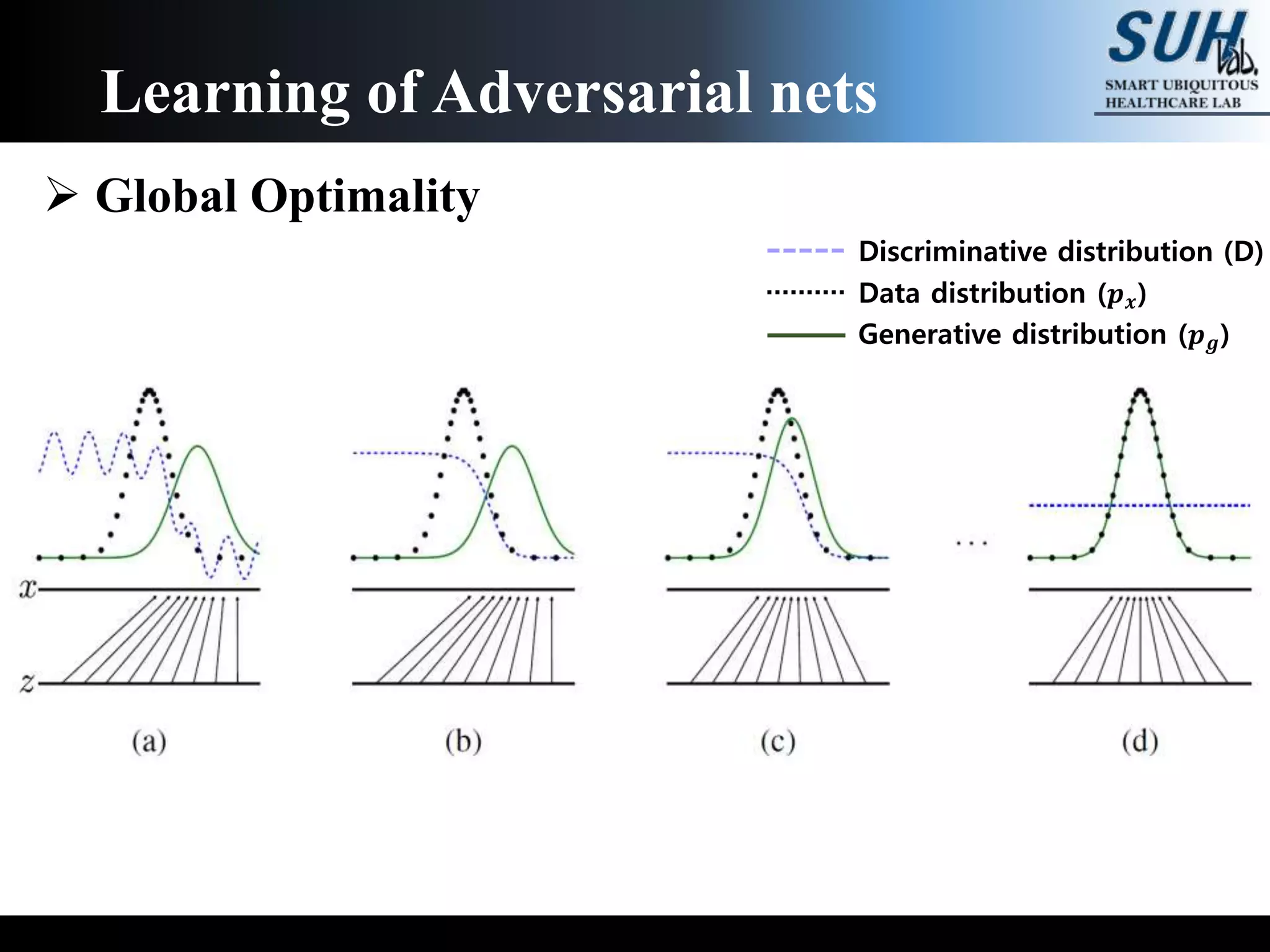
![Learning of Adversarial nets
Learn generator’s distribution 𝒑 𝒈 over data x
min
𝐺
max
𝐷
𝑽(𝑫, 𝑮)
= 𝔼 𝒙~𝒑 𝒅𝒂𝒕𝒂(𝒙) 𝒍𝒐𝒈 𝑫 𝒙 + 𝔼 𝒛~𝒑 𝒛(𝒛)[𝒍𝒐𝒈 𝟏 − 𝑫 𝑮 𝒛 ]
Global optimum 𝒑 𝒈 = 𝒑 𝒅𝒂𝒕𝒂](https://image.slidesharecdn.com/reviewofgenerativeadversarialnets-190711044929/75/Review-of-generative-adversarial-nets-9-2048.jpg)