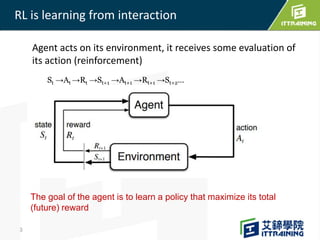
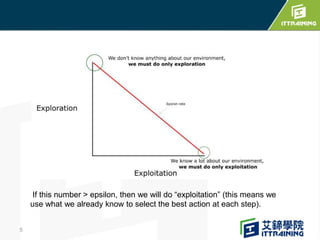
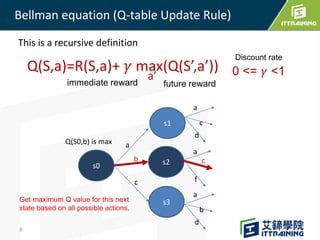
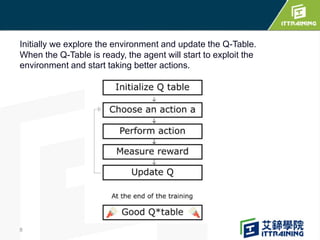
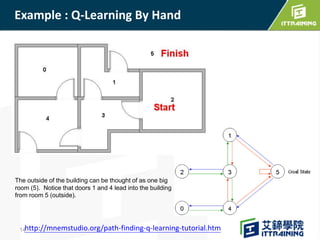
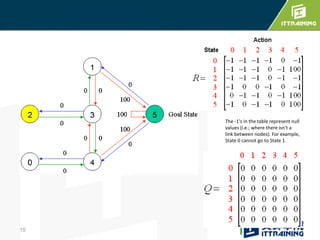
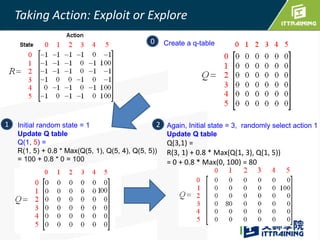
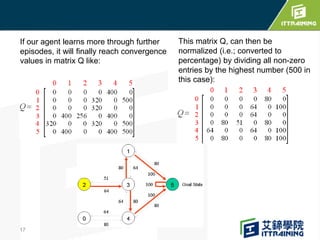
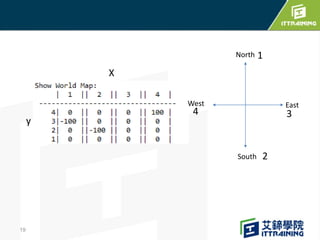
Reinforcement learning allows an agent to learn how to behave through trial-and-error interactions with an environment. The agent takes actions in a state and receives rewards, learning through experience which actions maximize total rewards. The agent learns a policy using a Q-table that represents the estimated utility of taking an action in a given state. Initially the agent explores randomly, but over time exploits what it has learned from the Q-table to select the highest-valued actions. The Q-learning algorithm iteratively updates the Q-table values using the Bellman equation to improve its estimates of the best actions.

1. Reinforcement Learning
from Explore to Exploit

2. Task: Learn how to behave successfully to achieve a
goal while interacting with an external environment
Learn via experiences!
Examples
• Game playing: player knows whether it win or lose, but
not know how to move at each step
• Control: a traffic system can measure the delay of cars,
but not know how to decrease it.
Reinforcement Learning
2

3. RL is learning from interaction
3
Agent acts on its environment, it receives some evaluation of
its action (reinforcement)
The goal of the agent is to learn a policy that maximize its total
(future) reward
St →At →Rt →St+1 →At+1 →Rt+1 →St+2…

4. At each State S, choose the a action a which
maximizes the function Q(S, a)
Q is the estimated utility function – it tells us how
good an action is given a certain state
Q-Learning Basics
4
所有決策都依據Q-table (best policy)，但Q table 要從何得來?

5. 5
If this number > epsilon, then we will do “exploitation” (this means we
use what we already know to select the best action at each step).

6. Bellman equation (Q-table Update Rule)
6
s0 s2
s1
s3
a
c
b
a
c
d
a
c
f
a
b
d
Q(S0,b) is max
Get maximum Q value for this next
state based on all possible actions.
0 <= 𝛾 <1Q(S,a)=R(S,a)+ 𝛾 max(Q(S’,a’))
a’immediate reward future reward
This is a recursive definition
Discount rate

7. Q(S,a)=R(S,a)+ 𝛾 max(Q(S’,a’))
𝛾=0.9
Example
7
reward=1
?

8. 8
Initially we explore the environment and update the Q-Table.
When the Q-Table is ready, the agent will start to exploit the
environment and start taking better actions.

9. This Q-table becomes a reference table for our agent to
select the best action
1. Set current state = initial state.
2. From current state, find the action with the highest Q value.
3. Set current state = next state.
4. Repeat Steps 2 and 3 until current state = goal state.
Algorithm to utilize the Q matrix:
9

10. 根據Q-table 走,
有可能有其他更
好的線但你不知
道, 也就是你可
能未必找到整體
的最佳路線!
10

11. Bellman equation 是看到當下狀態, 因此未必能能找到最
佳解, 故引入MDP方法以增加隨機性
只看Q-table 的值 (greedy method), 即永遠只做當下最好
的選擇,但未必最好。 故引入某種程度的隨機選擇，則有
機會去嘗試一條沒有走過的路，也許可以找到最佳的路
MDP (Markov Decision Process)
11

12. Q-Learning algorithm
12

13. Bellman equation
13
Note: 更新的是落差的部份..
NewQ(s,a)= (1-𝛼) Q(s,a) + 𝛼 {R (s,a)+ 𝛾 max(Q (s’, a’) }
0 <= 𝛾 < 1 Discount rate
0 <= 𝛼 <= 1 Learning rate

14. Example : Q-Learning By Hand
14http://mnemstudio.org/path-finding-q-learning-tutorial.htm
The outside of the building can be thought of as one big
room (5). Notice that doors 1 and 4 lead into the building
from room 5 (outside).

15. 15
The -1's in the table represent null
values (i.e.; where there isn't a
link between nodes). For example,
State 0 cannot go to State 1.

16. Taking Action: Exploit or Explore
16
Again, Initial state = 3, randomly select action 1
Update Q table
Q(3,1) =
R(3, 1) + 0.8 * Max(Q(1, 3), Q(1, 5))
= 0 + 0.8 * Max(0, 100) = 80
Initial random state = 1
Update Q table
Q(1, 5) =
R(1, 5) + 0.8 * Max(Q(5, 1), Q(5, 4), Q(5, 5))
= 100 + 0.8 * 0 = 100
1 2
Create a q-table0

17. 17
If our agent learns more through further
episodes, it will finally reach convergence
values in matrix Q like:
This matrix Q, can then be
normalized (i.e.; converted to
percentage) by dividing all non-zero
entries by the highest number (500 in
this case):

18. 實作
18

19. 19
X
y
North
South
EastWest
1
4
2
3