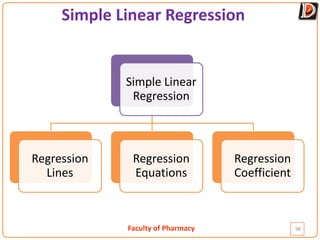
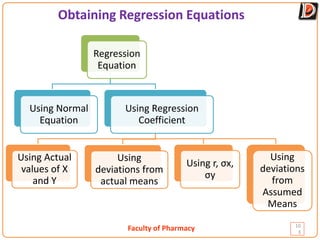
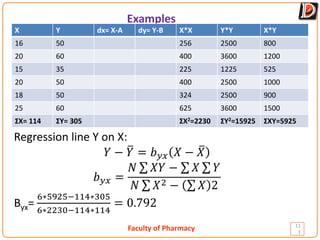
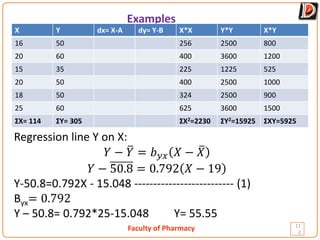
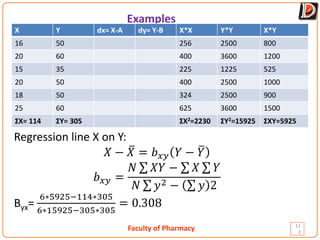
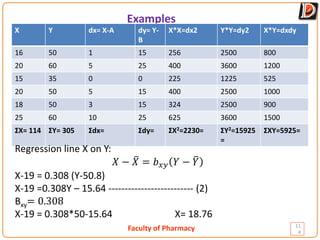
Regression is a statistical method used to analyze the relationship between two or more variables. It allows one to predict the value of a dependent variable based on the value of an independent variable. The document discusses simple linear regression, defining key concepts like the regression line, regression equations, and regression coefficients. It also provides an example to demonstrate calculating a regression line and using it to predict values.

1. Faculty of Pharmacy
Regression
92

2. Faculty of Pharmacy
What is Regression?
• Regression is the measure of the average
relationship between two or more variables.
• Regression Analysis measures the nature and
extent of the relationship between two or more
variables, thus enables us to make predictions.
93

3. Faculty of Pharmacy
Application of Regression
• Degree & Nature of relationship
• Estimation of relationship
• Prediction
• Useful in Economic & Business Research
94

4. Faculty of Pharmacy
DIFFERENCE BETWEEN CORRELATION
& REGRESSION
• Degree & Nature of Relationship
• Correlation is a measure of degree of relationship
between X & Y
• Regression studies the nature of relationship between the
variables so that one may be able to predict the value of
one variable on the basis of another.
• Cause & Effect Relationship
• Correlation does not always assume cause and effect
relationship between two variables.
• Regression clearly expresses the cause and effect
relationship between two variables. The independent
variable is the cause and dependent variable is effect.
95

5. Faculty of Pharmacy
DIFFERENCE BETWEEN CORRELATION
& REGRESSION
• Prediction
• Correlation doesn’t help in making predictions
• Regression enable us to make predictions using regression
line
• Symmetric
• Correlation coefficients are symmetrical i.e. rxy = ryx.
• Regression coefficients are not symmetrical i.e. bxy ≠ byx.
• Origin & Scale
• Correlation is independent of the change of origin and
scale
• Regression coefficient is independent of change of origin
but not of scale
96

6. Faculty of Pharmacy
Types of Regression Analysis
• Simple & Multiple Regression
• Linear & Non Linear Regression
• Partial & Total Regression
97

7. Faculty of Pharmacy
Simple Linear Regression
Simple Linear
Regression
Regression
Lines
Regression
Equations
Regression
Coefficient
98

8. Faculty of Pharmacy
Regression Lines
99
• The regression line shows the average relationship between
two variables. It is also called Line of Best Fit.
• If two variables X & Y are given, then there are two regression
lines:
• Regression Line of X on Y
• Regression Line of Y on X
• Nature of Regression Lines
• If r = ±1, then the two regression lines are coincident.
• If r = 0, then the two regression lines intersect each other at
90°.
• The nearer the regression lines are to each other, the greater
will be the degree of correlation.
• If regression lines rise from left to right upward, then
correlation is positive.

9. Faculty of Pharmacy
Regression Equations
10
0
• Regression Equations are the algebraic formulation of regression lines.
• There are two regression equations:
• Regression Equation of Y on X
Y = a + bX
𝑌𝑌 − �
𝑌𝑌 = 𝑏𝑏𝑏𝑏𝑏𝑏(𝑋𝑋 − �
𝑋𝑋)
𝑌𝑌 − �
𝑌𝑌 = 𝑟𝑟.
𝜎𝜎𝑦𝑦
𝜎𝜎𝑥𝑥
(𝑋𝑋 − �
𝑋𝑋)
• Regression Equation of X on Y
X = a + bY
𝑋𝑋 − �
𝑋𝑋 = 𝑏𝑏𝑏𝑏𝑏𝑏(𝑌𝑌 − �
𝑌𝑌)
𝑋𝑋 − �
𝑋𝑋 = 𝑟𝑟.
𝜎𝜎𝑥𝑥
𝜎𝜎𝑦𝑦
(𝑌𝑌 − �
𝑌𝑌)

10. Faculty of Pharmacy
Regression Coefficients
10
1
• Regression coefficient measures the average
change in the value of one variable for a unit
change in the value of another variable.
• These represent the slope of regression line
• There are two regression coefficients:
• Regression coefficient of Y on X: byx = 𝑟𝑟. σ𝑦𝑦/σ𝑥𝑥
• Regression coefficient of X on Y: bxy = 𝑟𝑟. σ𝑥𝑥/σ𝑦𝑦

11. Faculty of Pharmacy
Properties of Regression Coefficients
10
2
• Coefficient of correlation is the geometric mean of the
regression coefficients. i.e. r = 𝑏𝑏𝑥𝑥𝑥𝑥. 𝑏𝑏𝑦𝑦𝑦𝑦
• Both the regression coefficients must have the same
algebraic sign.
• Coefficient of correlation must have the same sign as that
of the regression coefficients.
• Both the regression coefficients cannot be greater than
unity.
• Arithmetic mean of two regression coefficients is equal to
or greater than the correlation coefficient.
• i.e. 𝑏𝑏𝑥𝑥𝑦𝑦+𝑏𝑏𝑦𝑦𝑥𝑥/2 ≥ r
• Regression coefficient is independent of change of origin
but not of scale.

12. Faculty of Pharmacy
Obtaining Regression Equations
10
3
Regression
Equation
Using Normal
Equation
Using Regression
Coefficient
Using Actual
values of X
and Y
Using
deviations from
actual means
Using r, σx,
σy
Using
deviations
from
Assumed
Means

13. Faculty of Pharmacy
Regression Equations in Individual Series Using Normal
Equations
10
4
• This method is also called as Least Square Method.
• In this method, regression equations can be calculated by
solving two normal equations:
• For regression equation Y on X: Y = a + bX
• Σ𝑌𝑌=𝑁𝑁𝑎𝑎+𝑏𝑏Σ𝑋𝑋
• Σ𝑋𝑋𝑌𝑌=𝑎𝑎Σ𝑋𝑋+𝑏𝑏Σ𝑋𝑋2
• Another Method:
• 𝑏𝑏𝑦𝑦𝑦𝑦 =
𝑁𝑁 ∑ 𝑋𝑋𝑋𝑋−∑ 𝑋𝑋 ∑ 𝑌𝑌
∑ 𝑋𝑋2− ∑ 𝑋𝑋 2
• Here a is the Y – intercept, indicates the minimum value of
Y for X = 0
• b is the slope of the line, indicates the absolute increase in
Y for a unit increase in X.

14. Faculty of Pharmacy
Regression Equations in Individual Series Using Normal
Equations
10
5
• For regression equation X on Y: X = a + bY
• ΣX=𝑁𝑁𝑎𝑎+𝑏𝑏ΣY
• Σ𝑋𝑋𝑌𝑌=𝑎𝑎ΣY+𝑏𝑏ΣY2
• Another Method:
• 𝑏𝑏𝑥𝑥𝑥𝑥 =
𝑁𝑁 ∑ 𝑋𝑋𝑋𝑋−∑ 𝑋𝑋 ∑ 𝑌𝑌
∑ 𝑌𝑌2− ∑ 𝑌𝑌 2
• Here a is the X – intercept, indicates the
minimum value of X for Y = 0
• b is the slope of the line, indicates the absolute
increase in X for a unit increase in Y.

15. Faculty of Pharmacy
Regression Equations Using Regression Coefficients
(Using Actual Values)
10
6
• Regression Equation of Y on X
𝑌𝑌 − �
𝑌𝑌 = 𝑏𝑏𝑏𝑏𝑏𝑏(𝑋𝑋 − �
𝑋𝑋)
• Regression Equation of X on Y
𝑋𝑋 − �
𝑋𝑋 = 𝑏𝑏𝑏𝑏𝑏𝑏(𝑌𝑌 − �
𝑌𝑌)

16. Faculty of Pharmacy
Regression Equations Using Regression Coefficients
(Using Deviations Actual Values)
10
7
• Regression Equation of Y on X
𝑌𝑌 − �
𝑌𝑌 = 𝑏𝑏𝑏𝑏𝑏𝑏(𝑋𝑋 − �
𝑋𝑋)
𝑏𝑏𝑦𝑦𝑦𝑦 =
∑ 𝑥𝑥𝑥𝑥
∑ 𝑥𝑥2
• Regression Equation of X on Y
𝑋𝑋 − �
𝑋𝑋 = 𝑏𝑏𝑏𝑏𝑏𝑏 𝑌𝑌 − �
𝑌𝑌
𝑏𝑏𝑥𝑥𝑥𝑥 =
∑ 𝑥𝑥𝑥𝑥
∑ 𝑦𝑦2

17. Faculty of Pharmacy
Regression Equations Using Regression Coefficients
(Using Deviations from Assumed Mean)
10
8
• Regression Equation of Y on X
𝑌𝑌 − �
𝑌𝑌 = 𝑏𝑏𝑏𝑏𝑏𝑏(𝑋𝑋 − �
𝑋𝑋)
𝑏𝑏𝑦𝑦𝑦𝑦 =
𝑁𝑁 ∑ 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 − ∑ 𝑑𝑑𝑑𝑑 ∑ 𝑑𝑑𝑑𝑑
𝑁𝑁 ∑ 𝑑𝑑𝑑𝑑2 − ∑ 𝑑𝑑𝑑𝑑 2
• Regression Equation of X on Y
𝑋𝑋 − �
𝑋𝑋 = 𝑏𝑏𝑏𝑏𝑏𝑏 𝑌𝑌 − �
𝑌𝑌
𝑏𝑏𝑥𝑥𝑦𝑦 =
𝑁𝑁 ∑ 𝑑𝑑𝑑𝑑𝑑𝑑𝑑𝑑 − ∑ 𝑑𝑑𝑑𝑑 ∑ 𝑑𝑑𝑑𝑑
𝑁𝑁 ∑ 𝑑𝑑𝑦𝑦2 − ∑ 𝑑𝑑𝑦𝑦 2

18. Faculty of Pharmacy
Regression Equations Using Regression Coefficients
(Using Standard Deviations)
10
9
• Regression Equation of Y on X
𝑌𝑌 − �
𝑌𝑌 = 𝑏𝑏𝑏𝑏𝑏𝑏(𝑋𝑋 − �
𝑋𝑋)
𝑏𝑏𝑦𝑦𝑦𝑦 = 𝑟𝑟.
𝜎𝜎𝑦𝑦
𝜎𝜎𝑥𝑥
• Regression Equation of X on Y
𝑋𝑋 − �
𝑋𝑋 = 𝑏𝑏𝑏𝑏𝑏𝑏 𝑌𝑌 − �
𝑌𝑌
𝑏𝑏𝑥𝑥𝑦𝑦 = 𝑟𝑟.
𝜎𝜎𝑥𝑥
𝜎𝜎𝑦𝑦

19. Faculty of Pharmacy
Examples
11
0
• Example 1: From following data calculate the
lines of regression.
• Estimate value of Y when X= 25
• Estimate value of X when Y= 50
X 16 20 15 20 18 25
Y 50 60 35 50 50 60

20. Faculty of Pharmacy
Examples
11
1
X Y dx= X-A dy= Y-B X*X Y*Y X*Y
16 50 256 2500 800
20 60 400 3600 1200
15 35 225 1225 525
20 50 400 2500 1000
18 50 324 2500 900
25 60 625 3600 1500
ƩX= 114 ƩY= 305 ƩX2=2230 ƩY2=15925 ƩXY=5925
Regression line Y on X:
𝑌𝑌 − �
𝑌𝑌 = 𝑏𝑏𝑦𝑦𝑦𝑦 𝑋𝑋 − �
𝑋𝑋
𝑏𝑏𝑦𝑦𝑦𝑦 =
𝑁𝑁 ∑ 𝑋𝑋𝑋𝑋 − ∑ 𝑋𝑋 ∑ 𝑌𝑌
𝑁𝑁 ∑ 𝑋𝑋2 − ∑ 𝑋𝑋 2
Byx=
6∗5925−114∗305
6∗2230−114∗114
= 0.792

21. Faculty of Pharmacy
Examples
11
2
X Y dx= X-A dy= Y-B X*X Y*Y X*Y
16 50 256 2500 800
20 60 400 3600 1200
15 35 225 1225 525
20 50 400 2500 1000
18 50 324 2500 900
25 60 625 3600 1500
ƩX= 114 ƩY= 305 ƩX2=2230 ƩY2=15925 ƩXY=5925
Regression line Y on X:
𝑌𝑌 − �
𝑌𝑌 = 𝑏𝑏𝑦𝑦𝑦𝑦 𝑋𝑋 − �
𝑋𝑋
𝑌𝑌 − 50.8 = 0.792 𝑋𝑋 − 19
Y-50.8=0.792X - 15.048 -------------------------- (1)
Byx= 0.792
Y – 50.8= 0.792*25-15.048 Y= 55.55

22. Faculty of Pharmacy
Examples
11
3
X Y dx= X-A dy= Y-B X*X Y*Y X*Y
16 50 256 2500 800
20 60 400 3600 1200
15 35 225 1225 525
20 50 400 2500 1000
18 50 324 2500 900
25 60 625 3600 1500
ƩX= 114 ƩY= 305 ƩX2=2230 ƩY2=15925 ƩXY=5925
Regression line X on Y:
𝑋𝑋 − �
𝑋𝑋 = 𝑏𝑏𝑥𝑥𝑥𝑥 𝑌𝑌 − �
𝑌𝑌
𝑏𝑏𝑥𝑥𝑥𝑥 =
𝑁𝑁 ∑ 𝑋𝑋𝑋𝑋 − ∑ 𝑋𝑋 ∑ 𝑌𝑌
𝑁𝑁 ∑ 𝑦𝑦2 − ∑ 𝑦𝑦 2
Byx=
6∗5925−114∗305
6∗15925−305∗305
= 0.308

23. Faculty of Pharmacy
Examples
11
4
X Y dx= X-A dy= Y-
B
X*X=dx2 Y*Y=dy2 X*Y=dxdy
16 50 1 15 256 2500 800
20 60 5 25 400 3600 1200
15 35 0 0 225 1225 525
20 50 5 15 400 2500 1000
18 50 3 15 324 2500 900
25 60 10 25 625 3600 1500
ƩX= 114 ƩY= 305 Ʃdx= Ʃdy= ƩX2=2230= ƩY2=15925
=
ƩXY=5925=
Regression line X on Y:
𝑋𝑋 − �
𝑋𝑋 = 𝑏𝑏𝑥𝑥𝑦𝑦 𝑌𝑌 − �
𝑌𝑌
X-19 = 0.308 (Y-50.8)
X-19 =0.308Y – 15.64 -------------------------- (2)
Bxy= 0.308
X-19 = 0.308*50-15.64 X= 18.76

24. Faculty of Pharmacy
Examples
11
5
• Example 2: from following data calculate the
lines of regression.
• Correlation coefficient value is 0.8= r
• Estimate value of Y when X= 60
• Estimate value of X when Y= 80
Mean S.D
X 50 5
Y 20 4

25. Faculty of Pharmacy
Examples
11
6
• We have
• �
𝑋𝑋 = 50
• �
𝑌𝑌 = 20
• σX = 5
• σY = 4
• 𝑏𝑏𝑦𝑦𝑦𝑦 = 𝑟𝑟
𝜎𝜎𝑦𝑦
𝜎𝜎𝑥𝑥
= 0.8 ∗
4
5
= 0.64
• 𝑏𝑏𝑥𝑥𝑥𝑥 = 𝑟𝑟
𝜎𝜎𝑥𝑥
𝜎𝜎𝑦𝑦
= 0.8 ∗
5
4
= 1

26. Faculty of Pharmacy
Examples
11
7
• We have
• �
𝑋𝑋 = 50
• �
𝑌𝑌 = 20
• σX = 5
• σY = 4
• 𝑏𝑏𝑦𝑦𝑦𝑦 = 𝑟𝑟
𝜎𝜎𝑦𝑦
𝜎𝜎𝑥𝑥
= 0.8 ∗
4
5
= 0.64
• 𝑏𝑏𝑥𝑥𝑥𝑥 = 𝑟𝑟
𝜎𝜎𝑥𝑥
𝜎𝜎𝑦𝑦
= 0.8 ∗
5
4
= 1