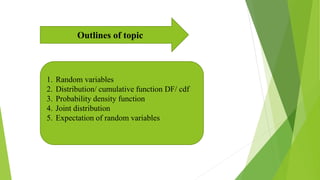
This document discusses random variables for discrete cases. It provides outlines on topics such as random variables, distribution/cumulative functions, probability density functions, joint distributions, and expectations of random variables. Examples are given for each topic. Applications in electrical engineering, civil engineering, and business are also discussed. These include using discrete random variables to find the probability of circuits being accepted or rejected, the number of defective circuits, and the number of working communication lines in a business.

1. Ali Zar 14093122-027
Aqeel Haider 14093122-017
Shahbaz Sharif 14093122-010
Electrical Engineering, 5th
University of Gujrat, Hafiz Hayat campus,
Gujrat
Group members

2. Topic of representation
Random variables for
discrete case

3. Outlines of topic
1. Random variables
2. Distribution/ cumulative function DF/ cdf
3. Probability density function
4. Joint distribution
5. Expectation of random variables

4. Random variables
 Such a numerical quantity whose value is determined
by the outcome of a random experiment, is called a
random variable.
 A random variable is a variable that is subject to
randomness, which means it can take on different
values.
 A random variable is also called chance variable, and
is abbreviated as r.v.
 The random variables are denoted by capital letters
as X, Y, Z and values taken by them as x,y,z.
 Two types of r.v :
1. The discrete
2. The continuous

5. Example
When two coins are tossed, we may be interested only
in the number of heads.
𝑆 = { 𝐻𝐻, 𝐻𝑇, 𝑇𝐻, 𝑇𝑇}

6. Distribution/ cumulative
function DF/ cdf
The distribution function of a random variable X,
denoted by F(x), defined by F(x)= P(X<=x).
 F(x) gives the probability of the event that X
takes a value less than or equal to a specified
value x.
F(x) is a non decreasing function of x.
F −∞ = 0, F +∞ = 1.

7. Example
Suppose, three coins are tossed and ‘x’ is
number of tails. Find probability distribution
and construct its graph.

8. Joint distribution
 Distribution of more than one variables.
 We study only Bivariate ( two variables).
 Important terms in joint distribution are:
 Marginal of x (only interested in x, g(x)) and
 Marginal of y (only interested in y, h(y)).
 𝑔 𝑥 = 𝑦 𝑓(𝑥, 𝑦)
 ℎ 𝑦 = 𝑥 𝑓(𝑥, 𝑦)

9. How to calculate?
f(x)
1. 0 ≤ 𝑓 𝑥 ≤ 1
2. 𝑓 𝑥 = 1
f(x, y)
1. 0 ≤ 𝑓 𝑥, 𝑦 ≤ 1
2. 𝑓 𝑥, 𝑦 = 1

10. Expectation of random
variables
The expected value of X, denoted by E(X), is
defined as:
𝐸 𝑋 = 𝑥1f 𝑥1 + 𝑥2 𝑓 𝑥2 + ⋯ + 𝑥 𝑛 𝑓 𝑥 𝑛
E(X) is also called the mean of X and is usually
denoted by 𝜇.

11. How to calculate?
𝐸 𝑋 = 𝑥 𝑓 𝑥
𝐸 𝑋2 = 𝑥2 𝑓(𝑥)
𝐸 𝑥 + 𝑦 = 𝑥 + 𝑦 𝑓(𝑥, 𝑦)
𝐸 𝑥. 𝑦 = 𝑥. 𝑦 𝑓(𝑥, 𝑦)
𝐸 𝑋 = 𝑥. 𝑔(𝑥)
𝐸 𝑌 = 𝑦. ℎ(𝑦)
𝑉𝑎𝑟 𝑋 = 𝐸 𝑋2 − [𝐸 𝑥 ]2

12. Applications in
Electrical Engineering

13. Application 1
If we want to find probability of circuits accepted or not.
if number of given integrated circuit would be accepted
or rejected we use discrete PMF.

14. Application 2
If we want to find number of semiconductor wafers that
need to be analyzed in order to detect a large particle of
contamination in p-type or n-type material or in doping
material we use random variables or discrete random
variable.

15. Application 3
If we have number of circuit and we need the probability
to test circuit to be defective and non-defective we use
discrete variable distribution to find the number of
defective and non-defective circuits.

16. Applications in Civil
Engineering

17. Application 1
If we want to find load on a specific point in a beam we
can use discrete functions to find loading at each point
on a beam.
Suppose a loading on a long, thin beam places mass only
at discrete points. The loading can be described by a
function that specifies the mass at each of the discrete
points. Similarly, for a discrete random variable X, its
distribution can be described by a function that specifies
the probability at each of the possible discrete values for
X.

18. Application 2
Statisticians use sampling plans to either accept or reject
batches or lots of construction material.
Suppose one of these sampling plans involves sampling
independently 10 items from a lot of 100 items in which
12 are defective.

19. Applications in
Business

20. Application 1
In any business firm there is a communication system
with certain number of lines to communication data and
voice communication.
If we need to know the probability of how many lines
are working at one time we use discrete variables.

21. Thank you