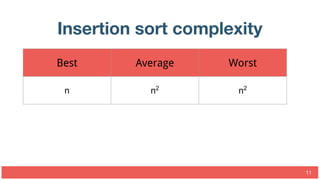
This document discusses different sorting algorithms and their complexities. It covers slow sorts like bubble sort and insertion sort which have quadratic time complexity, as well as medium sorts like merge sort which has linearithmic time complexity. Merge sort works by dividing the array into sublists of one element and then merging the sublists together until the entire list is sorted. The document provides pseudocode examples and analyses the time complexities of various sorting algorithms.

1. Data Structures and Algorithms -
Sorting algorithms
Abimbola Idowu
The Andela Institute

2. Introduction to Sorting
Algorithms

3. Why sorting algorithms
3
• Efficient sorting is important for the use of other
algorithms such as search
• The way data is sorted affects how fast it can be
traversed or searched for
• Poor choice of algorithms affect the runtime of our
code

4. Classifications
• Computation complexity
• Memory Usage
• Stability
• Comparison sort...
4

5. Part 1 - Slow sort

6. Bubble Sort
• Loop through the array
• Compares each pair of adjacent elements
• Swaps if they are in wrong order
• Repeat until no swap is done
• Array is sorted
6

7. Pseudocode
7
procedure bubbleSort( A : list of sortable items )
n = length(A)
repeat
swapped = false
for i = 1 to n-1 inclusive do
/* if this pair is out of order */
if A[i-1] > A[i] then
/* swap them and remember something changed */
swap( A[i-1], A[i] )
swapped = true
end if
end for
until not swapped
end procedure

8. Bubble sort complexity
8
Best Average Worst
n n2
n2

9. Insertion sort
• Loop through the array
• Pick an element in the array
• Find the location where it belongs in the array
• Continue till loops ends
• Array is sorted
9

10. Pseudocode
10
for i ← 1 to length(A) - 1
j ← i
while j > 0 and A[j-1] > A[j]
swap A[j] and A[j-1]
j ← j - 1
end while
end for

11. Insertion sort complexity
11
Best Average Worst
n n2
n2

12. Why is slow slow
12
• Comparison is local
• Guarantee to always make a lot of
comparison

13. Part 2 - Medium Sort

14. Merge Sort
• Divide the array in sublist until each sublist
contains one elements
• Merge sublists until there are one
• Array is sorted
14

15. Pseudocode
15
function merge(left, right)
var list result
while notempty(left) and notempty(right)
if first(left) <= first(right)
append first(left) to result
left = rest(left)
else
append first(right) to result
right = rest(right)
// either left or right may have elements left
while notempty(left)
append first(left) to result
left = rest(left)
while notempty(right)
append first(right) to result
right = rest(right)
return result

16. Merge sort complexity
16
Best Average Worst
n n logn n logn

17. Next time
• Other types of medium sorts
• Fast sorts
17