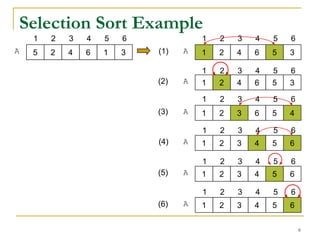
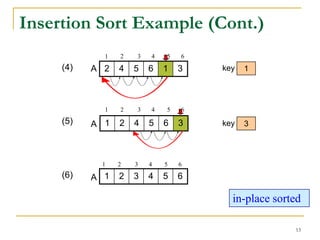
This document provides a summary of a lecture on sorting algorithms: 1) It introduces sorting concepts and sorting problems. Common sorting algorithms discussed include selection sort, insertion sort, merge sort, and quick sort. 2) Selection sort and insertion sort algorithms are explained in detail with examples. Selection sort has a running time of O(n^2) in all cases. 3) Insertion sort's running time depends on how sorted the input array is - it is O(n) for a presorted array but O(n^2) for a reverse sorted array. 4) The time complexity of both algorithms is analyzed mathematically. Selection sort is always O(n^2) while

1. 1302251 Data Structures and Algorithms
Lecture 11
Sorting
Aj. Khwunta Kirimasthong
School of Information Technology
Mae Fah Luang University

2. Outline
 Sorting Concept
 Sorting Algorithm
 Selection Sort
 Insertion Sort
 Merge Sort
 Quick Sort
2

3. Sorting Concept
 Sorting is the operation of arranging data in some
given order, such as
 Ascending
 the dictionary, the telephone book
 Descending
 grade-point average for honor students
 The sorted data can be numerical data or character
data.
 Sorting is one of the most common data-processing
applications.
3

4. Sorting Concept (Cont.)
 Sorting problem
Let A be a sequence of n elements. Sorting A refers
to the operation of rearranging the content of A so
that they are increasing in order.
Input: A: the sequence of n numbers ( a1 , a 2 , ..., a n )
Output: A: the reordering ( a1 , a 2 ,..., a n ) of the
input sequence such that
a1 a2 an
4

5. Selection Sort
 One of basic sorting algorithms
 Selection Sort works as follows:
 First, find the smallest elements in the data
sequence and exchange it with the element in the
first position,
 Then, find the second smallest element and
exchange it with the element in the second
position and
 Continue in this way until the entire sequence is
sorted.
5

6. Selection Sort Example
1 2 3 4 5 6 1 2 3 4 5 6
A 5 2 4 6 1 3 (1) A 1 2 4 6 5 3
1 2 3 4 5 6
(2) A 1 2 4 6 5 3
1 2 3 4 5 6
(3) A 1 2 3 6 5 4
1 2 3 4 5 6
(4) A 1 2 3 4 5 6
1 2 3 4 5 6
(5) A 1 2 3 4 5 6
1 2 3 4 5 6
(6) A 1 2 3 4 5 6
6

7. Selection Sort Algorithm
Algorithm SelectionSort(A,n)
Input: A: a sequence of n elements
n: the size of A
Output: A: a sorted sequence in ascending order
for i = 1 to n
min = i
for j = i+1 to n
if A[j] < A[min] then
min = j
Swap(A,min,i)
7

8. Selection Sort Algorithm (Cont.)
Algorithm: Swap(A,min,i)
Input: A : a sequence of n elements
min: the position of the minimum value of A
while considers at index i of A
i: the considered index of A
Output: exchange A[i] and A[min]
temp = a[min]
a[min] = a[i]
a[i] = temp
8

9. Selection Sort Analysis
 For i = 1, there are _(n-1)_ comparisons to find the
first smallest element.
 For i = 2, there are _(n-2)_ comparisons to find the
second smallest element, and so on.
 Accordingly, n 1
(n-1) + (n-2) + (n-3) + … + 2 + 1 = i = n(n-1)/2
i 1
 The best case running time is ___ (n2)__
 The worst case running time is __ O(n2)__
9

10. Insertion Sort
 To solve the sorting problem
 Insertion sort algorithm is almost as simple as
selection sort but perhaps more flexible.
 Insertion sort is the method people often
use for sorting a hand of cards.
10

11. Insertion Sort (Cont.)
 Insertion sort uses an incremental approach:
having the sorted subarray A[1…j-1], we
insert the single element A[ j ] into its proper
place and then we will get the sorted
subarray A[ 1…j ]
pick up
Sorted order Unsorted order
11

12. Insertion Sort Example
1 2 3 4 5 6
5 2 4 6 1 3
key = A[j]
1 2 3 4 5 6
(1) A 5 2 4 6 1 3 key 2
1 2 3 4 5 6
(2) A 2 5 4 6 1 3 key 4
1 2 3 4 5 6
(3) A 2 4 5 6 1 3 key 6
in-place sorted
12

13. Insertion Sort Example (Cont.)
1 2 3 4 5 6
(4) A 2 4 5 6 1 3 key 1
1 2 3 4 5 6
(5) A 1 2 4 5 6 3 key 3
1 2 3 4 5 6
(6) A 1 2 3 4 5 6
in-place sorted
13

14. Insertion Sort Algorithm
Algorithm: INSERTION-SORT(A)
Input: A : A sequence of n numbers
Output: A : A sorted sequence in increasing order of array A
for j = 2 to length(A)
key = A[j]
//Insert A[j] into the sorted sequence A[1…j-1]
i = j-1
while i > 0 and A[i] > key
A[i+1] = A[i]
i = i-1
A[i+1] = key
14

15. Insertion Sort Analysis
 The running – time of INSERTION-SORT
depends on the size of input.
15

16. Insertion Sort Analysis (cont.)
INSERTION-SORT(A) cost times
1. for j = 2 to length(A) c1 n
2. key = A[j] c2 n-1
3. //Insert A[j] into the sorted sequence A[1…j-1] 0 n-1
4. i = j-1 c4 n-1
n
5. while i > 0 and A[i] > key c5 tj
j 2
n
6. A[i+1] = A[i] c6 (t j 1)
j 2
n
7. i = i-1 c7 (t j 1)
j 2
8. A[i+1] = key c8 n-1
16

17. Analysis of Insertion Sort (Cont.)
 To Compute the total running time of INSERTION-
SORT, T ( n )
n
T (n) c1 n c2 (n 1) 0(n 1) c4 (n 1) c5 tj
j 2
n n
c6 (t j 1) c7 (t j 1) c8 ( n 1)
j 2 j 2
17

18. Analysis of Insertion Sort (Cont.)
 Best – case
 If input array is already sorted. Thus tj = 1
T(n) = c1n+c2(n-1)+(0)(n-1)+c4(n-1)+c5(n-1)+c6(0)+c7(0)+c8(n-1)
= (c1+c2+c3+c4+c5+c8)n - (c2+c3+c4+c5+c8)
an + b for constant a and b
Base-case running time of INSERTION-SORT is (n)
18

19. Analysis of Insertion Sort (Cont.)
 Worse – case
 If input array is in reverse sorted order. Thus tj = j
n(n 1)
T (n) c1 n c2 (n 1) c4 (n 1) c5 1
2
(n 1) n (n 1) n
c6 c7 c8 ( n 1)
2 2
c5 c6 c6 2 c5 c6 c7
T (n) n c1 c2 c4 c8 n
2 2 2 2 2 2
(c2 c4 c5 c8 ) an
2
bn c
for constant a, b and c
2
Worse-case running time of INSERTION-SORT is (n )
19

20. Analysis of Insertion Sort (Cont.)
 Worse – case (Cont.)
 If input array is in reverse sorted order. Thus tj = j
n
n n n(n 1)
n(n 1) j
tj j 1 j 1
2
j 2 j 2 2
n n
(n 1)(( n 1) 1) (n 1) n
(t j 1) (j 1) (1 1)
j 2 j 2 2 2
20

21. Divide and Conquer
Approach
Merge Sort
Quick Sort

22. Divide-and-Conquer Approach
 The divide-and-conquer approach involves
three steps at each level of the recursion:
 Divide the problem into a number of sub-problems
that are similar to the original problem but smaller
in size.
 Conquer the sub-problems by solving them
recursively.
 Combine the solution of subproblems into the
solution for the original problem.
22

23. Merge Sort
 The Merge Sort algorithm closely follows the
divide-and-conquer approach. It operates as
follows,
 Divide: Divide the n-element sequence to be
sorted into two subsequences of n/2 elements
each.
 Conquer: Sort the two subsequences recursively
using merge sort
 Combine: Merge the two sorted subsequences to
produce the sorted solution.
23

24. Merge Sort (Cont.)
 The recursion “bottom out” when the
sequence to be sorted has length 1, in which
case there is no work to be done, since every
sequence of length 1 is already in sorted
order.
24

25. Merge Sort Example DIVIDE
&
0 1 2 3 4 5 CONQUER
A 5 2 4 6 1 3
0 1 2 3 4 5
5 2 4 6 1 3
0 1 2 3 4 5
5 2 4 6 1 3
0 1 3 4
5 2 6 1
25

26. Merge Sort Example (cont.)
0 1 2 3 4 5
COMBINE
A 1 2 3 4 5 6
0 1 2 3 4 5
2 4 5 1 3 6
0 1 2 3 4 5
2 5 4 1 6 3
0 1 3 4
5 2 6 1
26

27. Merge Sort Algorithm
Algorithm MergeSort( A, p, q )
Input: A: a sequence of n elements
p: the beginning index of A
q: the last index of A
Output: A: a sorted sequence of n elements
if(p < q) then
r = floor((p+q)/2)
MergeSort(A,p,r)
MergeSort(A,r+1,q)
Merge(A,p,r,q)
27

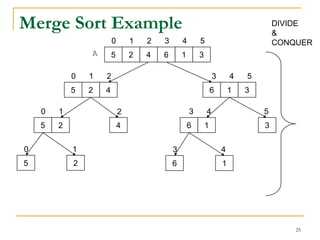
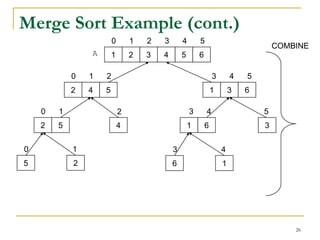
28. Algo Merge(A,p,r,q)
Input: A, p, r, q : a sorted subsequences A[p…r] and
A[r+1…q]
Output: A: a sorted sequence A[p…q]
let i=p, k=p, j=r+1
while (i ≤ r) and (j ≤ q)
if (A[i] ≤ A[j]) then
B[k] = A[i]
k++
i++
else
B[k] = A[j]
k=k+1
j=j+1
if (i>r) then /* If the maximum value of left subsequence is less than the right subsequence */
while(j ≤ q)
B[k] = A[j]
k++
j++
else if(j > q) then /* If the maximum value of left subsequence is gather than the right subsequence */
while(i ≤ r)
B[k] = A[i]
k++
i++
for k = p to q
A[k] = b[k]
28

29. Merge Sort Analysis
 The best case running time is _ (n log n)_
 The worst case running time is _ O(n log n) _
29

30. Quick Sort
 Quick Sort, likes merge sort, is based on the
divide-and-conquer approach.
 To sort an array A[p…r]
 Divide: Partition (rearrange) the array A[p…r] into
two subarray A[p…q -1] and subarray A[q+1…r]
such that:
 Each element of A[p…q -1] is less than or equal to A[q]
 Each element of A[q+1…r] is greater than A[q]
30

31. Quick Sort (Cont.)
 To sort sorting an array A[p…r] (cont.)
 Conquer: Sort the two subarray A[p…q -1] and
A[q+1…r] by recursive calls to QuickSort.
 Combine: Since the subarrays are sorted in place, no
work is needed to combine them: the entire array
A[p…r] is now sorted.
31

32. Quick Sort Example
0 1 2 3 4 5
A 5 2 4 6 1 3
32

33. Quick Sort Algorithm
Algo QuickSort(A, p, r)
Input: A: A sequence of n numbers
p: The first index of A
r: The last index of A
Output: A: A sorted sequence in increasing order of array A
• Rearrange the subarray
if (p < r) then A[p…r] in place.
• The elements that is less
q = Partition(A,p,r) than A[q] are placed at the
left side of A[q] and
QuickSort(A,p,q-1) • The elements that is
greater than A[q] are placed
QuickSort(A,q+1,r) at the right side of A[q].
33

34. Quick Sort Algorithm (Cont.)
Algo Partition(A, p, r)
Input: A: A sequence of n numbers
p: The first index of A
r: The last index of A
Output: A: The rearranged subarray A[p…r]
key = A[r]
i=p–1
for j = p to r -1
if A[ j ] ≤ key then
i = i+1
exchange A[i] and A[j]
exchange A[i+1] and key
return i+1 34

35. Quick Sort Analysis
 The best case running time is _ (n log n)_
 The worst case running time is _ O(n2)_
35

36. Q&A