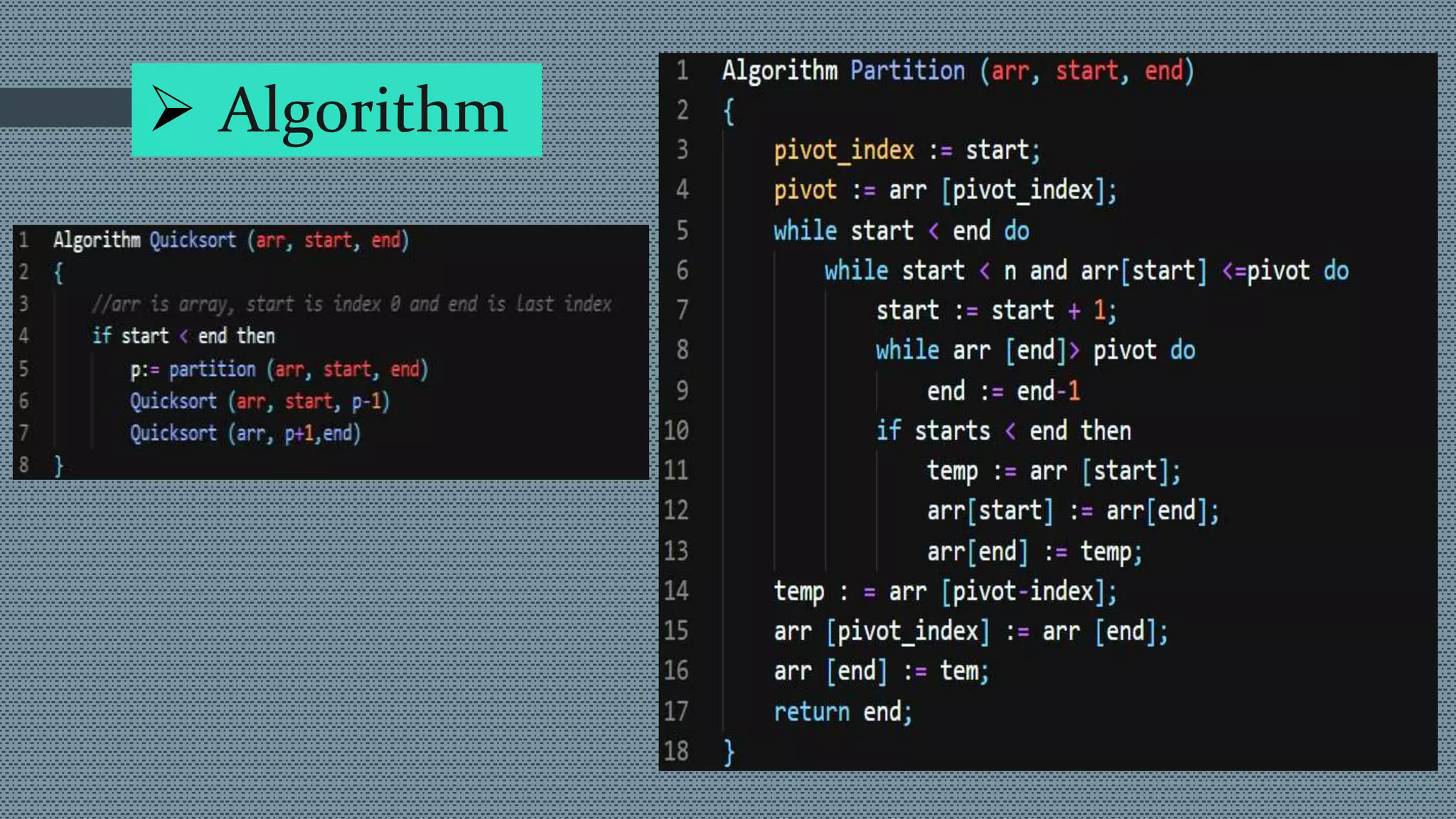
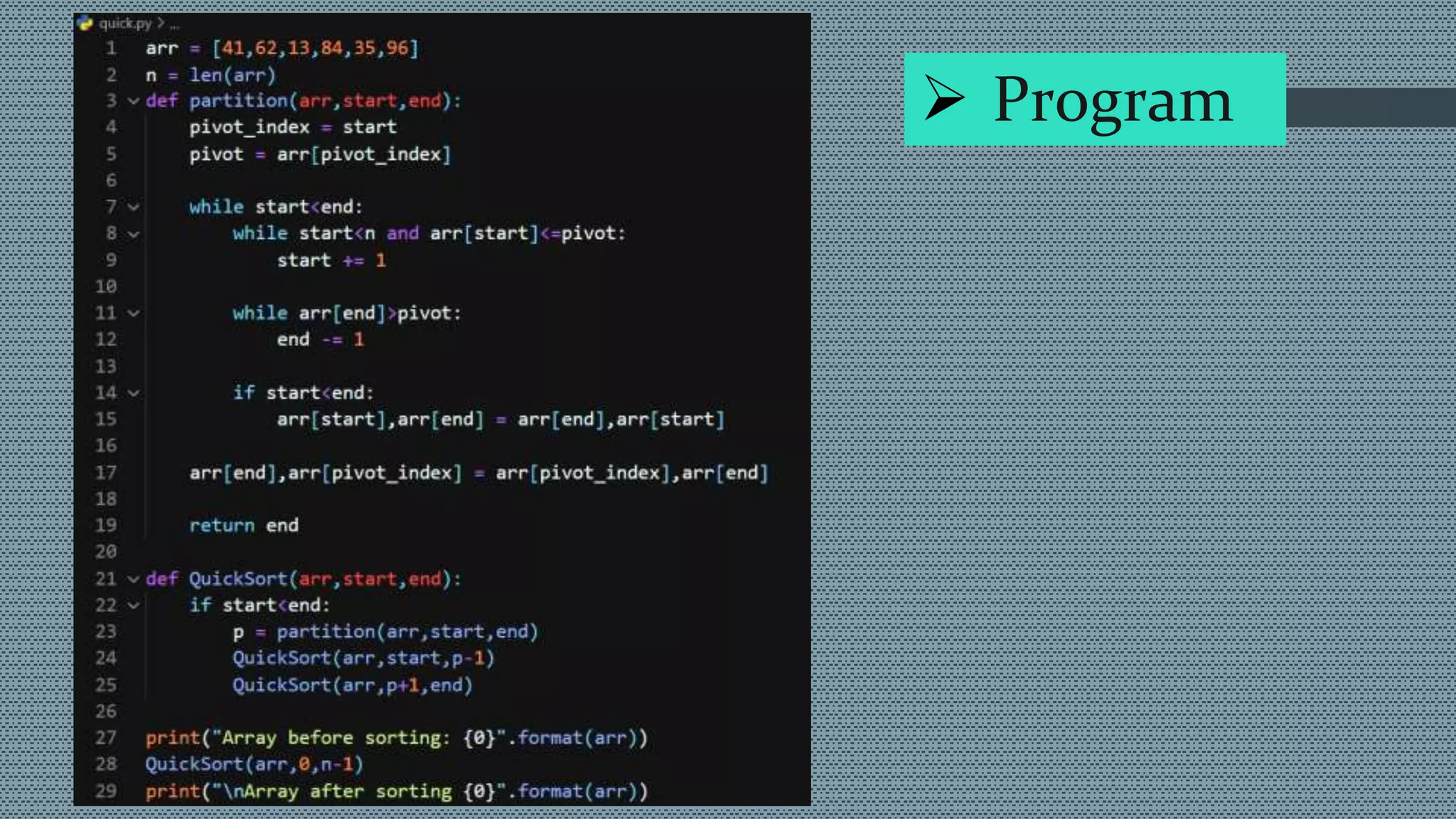
Quick sort is a widely used and efficient sorting algorithm that utilizes the divide and conquer strategy, partitioning an array into smaller arrays based on a specified pivot value. The algorithm sorts elements in place by recursively sorting sub-arrays and has a best and average time complexity of O(n log n), with a worst case of O(n^2). Space complexity can range from O(n) for the basic approach to O(log n) for the modified approach.

1. Quick Sort
Using
Divide And Conquer
Algorithm
Name : Mrunal Sanjay Patil
Roll No : FYMCA2064

2. What is Quick Sort ?
 Ranking manner Quick Sort is the most widely used of all the other sorting
algorithms because they are faster and consume less memory.
 Fastest known sorting algorithm in practice
 Quick sort is a highly efficient sorting algorithm and is based on partitioning of
array of data into smaller arrays.
 A large array is partitioned into two arrays one of which holds
values smaller than the specified value, say pivot, based on which the
partition is made and another array holds values greater than
the pivot value.

3. Divide and Conquer
Divide :
Divide the problem into a number of sub-problems
Similar sub-problems of smaller size
Conquer :
Conquer the sub-problems Solve the sub-problems
recursively.
Sub-problem size small enough  solve the problems in
straightforward manner
Combine :
Combine the solutions of the sub-problems
Obtain the solution for the original problem

4. How we use divide and conquer algorithm for
Quicksort
 Sort an array A[p…r]
 Divide
Partition the array A into 2 subarrays A[p..q] and A[q+1..r], such that each element of
A[p..q] is smaller than or equal to each element in A[q+1..r]
Need to find index q to partition the array
≤

5.  Conquer
Recursively sort A[p..q] and A[q+1..r] using Quicksort.
First sort A[p..q] and then sort A[q+1..r] individually.
 Combine
Trivial: the arrays are sorted in place
No additional work is required to combine them.
The entire array is now sorted.
≤

6. Basic idea (The first step towards sorting the
elements)
 Pick some number as pivot from the array
 Move all numbers less than pivot to the beginning of the array
 Move all numbers greater than (or equal to) pivot to the end of the array
 Quicksort the numbers less than pivot
 Quicksort the numbers greater than or equal to pivot
pivot
pivot
numbers less than pivot numbers greater than or equal to

7. Example
41 62 13 84 35 96
Pivot = 41 i j
35
84
13
62
41
If i > j then swap i and j Else j--
96
35
84
13
62
41
i j
41 > 35 = true
35
84
13
62
41
i j
swap 41 and 35
96
96
Unsorted array of 6 elements
41 > 96 = false then j--

8. i j
41
84
13
62
35 96
Pivot = j = 41 do i++
i j
62 > 41 = true
j
41
84
13
i
62
swap 41 and 62
j
62
84
13
i
41
Pivot = i = 41 do j--
35 35 96
41
84
13
62 84
62
35 96
96

9. 41 > 84 = false do j-- 41 > 13 = True
j
13
i
41 62
84
35
j
84
13
i
41 62
35 96
swap 41 and 13 Pivot = j = 41 do
96
j
41
i
13 62
84
35 96
j
13
i
41 62
84
35 96

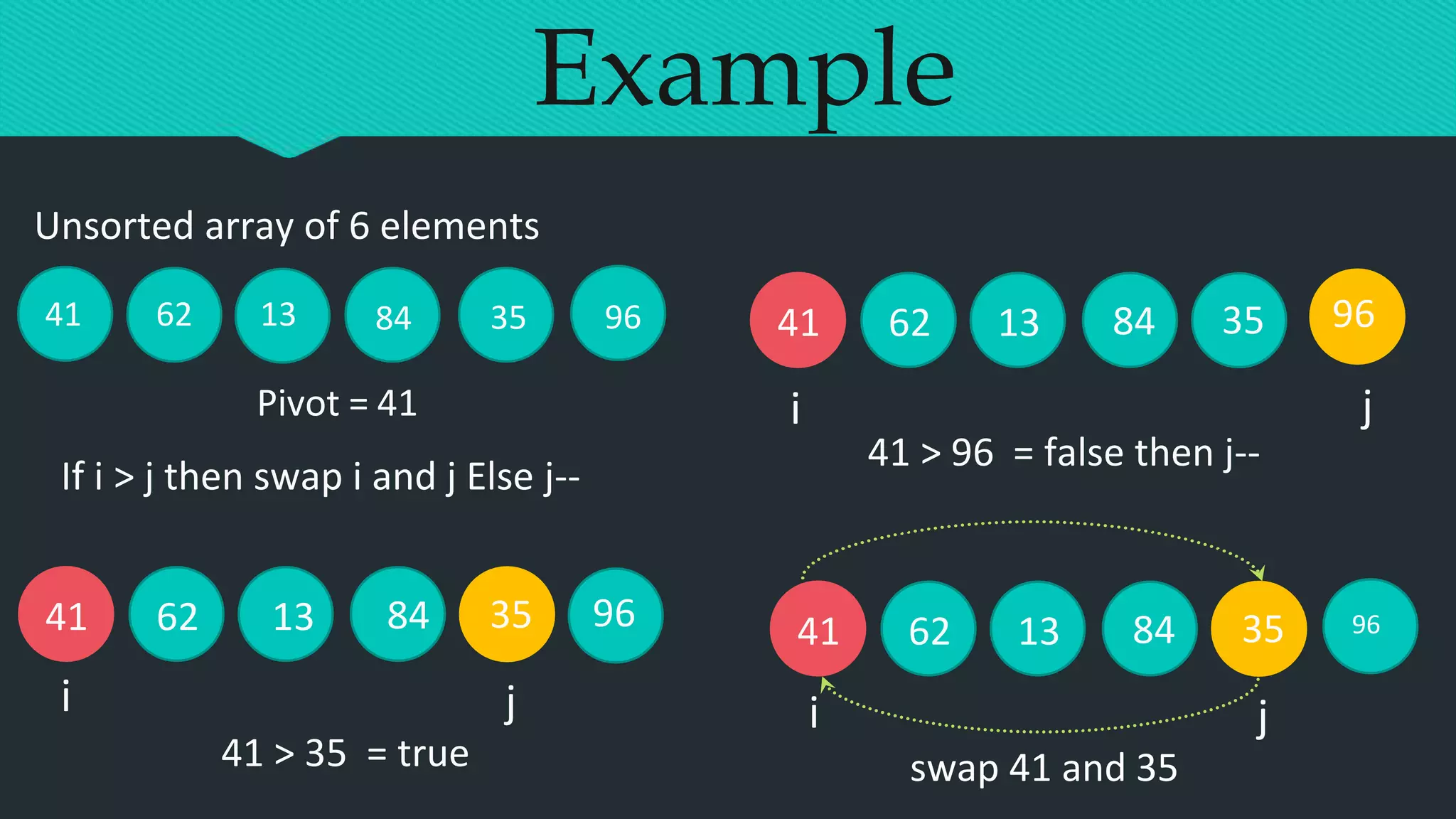
10. i = j
41
13
35
a[0] a[1] a[2] a[3] a[4] a[5]
numbers less than
pivot
numbers greater than or
equal to pivot
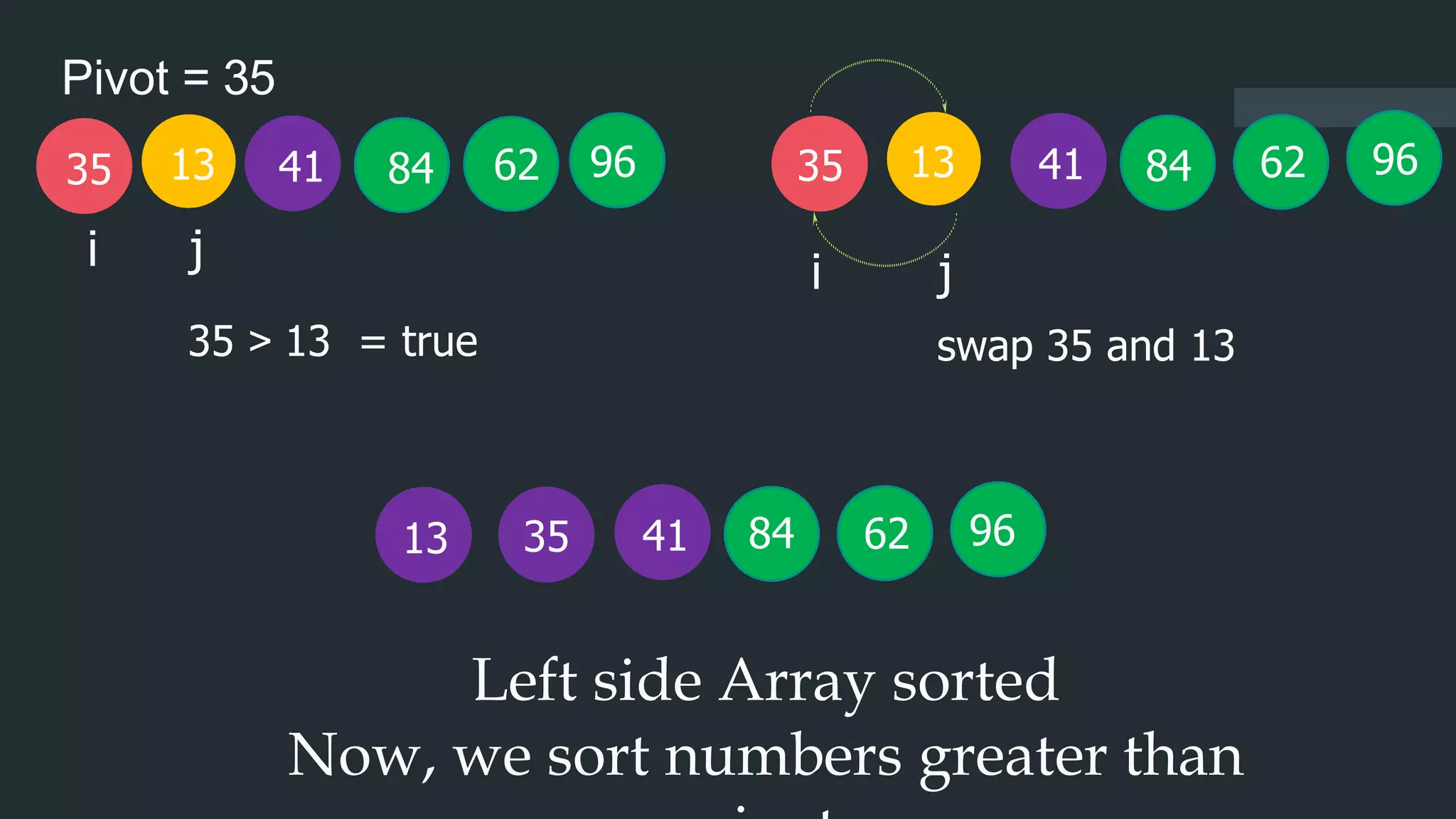
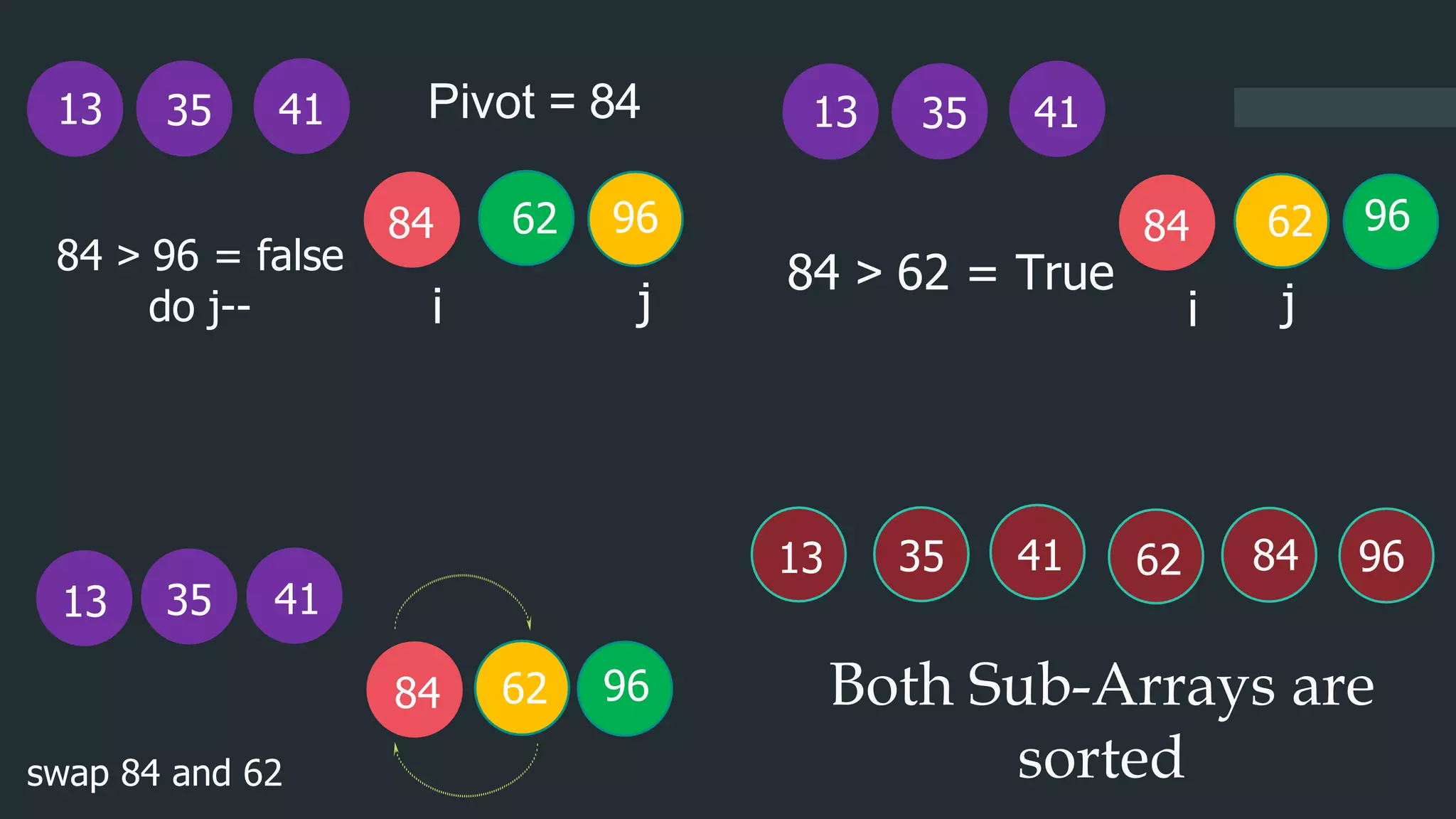
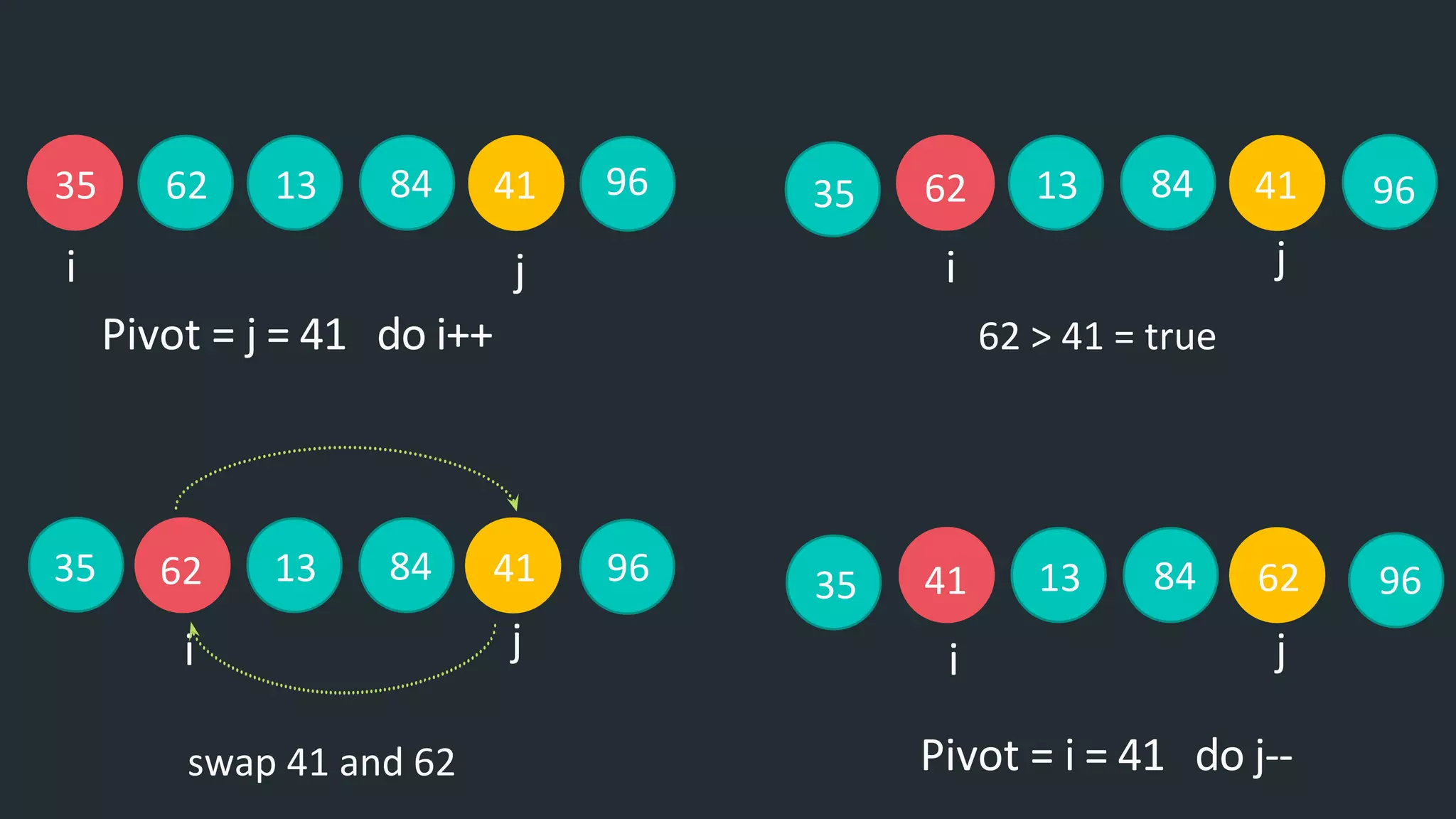
Now we sort numbers less than pivot
13
35
41 62
84 96
62
84 96
j
41
i
13 62
84
35 96

11. 13 41 62
84 96
Pivot = 35
j
i
35
35 > 13 = true
Left side Array sorted
Now, we sort numbers greater than
35 41 62
84
13 96
13 41 62
84
j
i
35 96
swap 35 and 13

12. 35 41
13
Pivot = 84
84 > 62 = True
35 41
13
swap 84 and 62
Both Sub-Arrays are
sorted
62
35 41
13
j
i
84
84 > 96 = false
do j--
96 62
j
i
84 96
62
84 96
35 41 84
13 62 96

13.  Algorithm

14.  Program

15. Quick Sort Space Complexity
 Basic approach : O(n)
 Modified approach : O(logn)
Quick Sort Time Complexity
 Best Time Complexity : O(nlogn)
 Average Time Complexity : O(nlogn)
 Worst Time Complexity : O(n^2)
The amount of computer time needs to run to completion.
The amount of computer space (memory) needs to
run to completion.