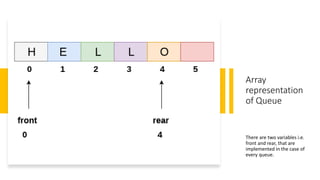
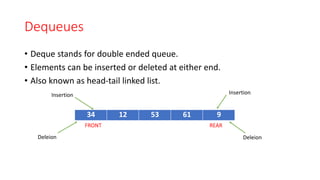
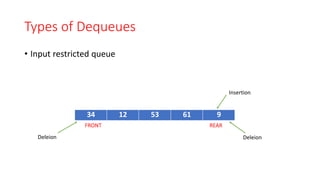
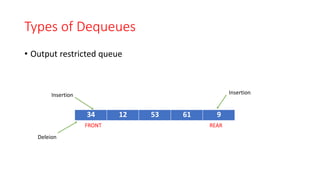
The document provides an introduction to queues, explaining that they are ordered collections where items are added at the rear and removed from the front, following a FIFO (First In First Out) principle. It details operations such as insertion (enqueue), deletion (dequeue), and outlines conditions for queue status (empty or full), as well as representations using arrays and linked lists. The document also discusses applications of queues in algorithms and operating systems.

1. Queues
UNIT II

2. Introduction to Queues
• A queue is an ordered collection of items where the addition of new items
happens at one end, called the “rear,” and the removal of existing items
occurs at the other end, commonly called the “front.”
• Queue: FIFO (Fist In First Out) : Enqueue and Dequeue, front, rear
• Stack: FILO or LIFO , Push and Pop, top

3. Array
representation
of Queue
There are two variables i.e.
front and rear, that are
implemented in the case of
every queue.

4. Maxsize=6, rear=front=-1
• Qinsert(item)
• 1.If (rear = maxsize-1 )
• print (“queue overflow”) and return
• 2.Else
• rear = rear + 1
• Queue [rear] = item
0 1 2 3 4 5
rear
front
Function call
Qinsert(item)
Rear=maxsize-1? Rear=rear+1 Queue[rear]=item
If section Else section

5. Maxsize=6, rear=0, front=-1
• Qinsert(item)
• 1.If (rear = maxsize-1 )
• print (“queue overflow”) and return
• 2.Else
• rear = rear + 1
• Queue [rear] = item
20
0 1 2 3 4 5
rear
front
Function call
Qinsert(item)
Rear=maxsize-1 Rear=rear+1 Queue[rear]=item
Qinsert(20) -1=5 ? F Rear=-1+1=0 Queue[0]=20
If section Else section
1

6. Maxsize=6, rear=1, front=-1
• Qinsert(item)
• 1.If (rear = maxsize-1 )
• print (“queue overflow”) and return
• 2.Else
• rear = rear + 1
• Queue [rear] = item
20 30
0 1 2 3 4 5
rear
front
Function call
Qinsert(item)
Rear=maxsize-1 Rear=rear+1 Queue[rear]=item
Qinsert(20) -1=5 ? F Rear=-1+1=0 Queue[0]=20
Qinsert(30) 0=5? F Rear= 0+1=1 Queue[1]=30
If section Else section
1
2

7. Maxsize=6, rear=2, front=-1
• Qinsert(item)
• 1.If (rear = maxsize-1 )
• print (“queue overflow”) and return
• 2.Else
• rear = rear + 1
• Queue [rear] = item
20 30 40
0 1 2 3 4 5
rear
front
Function call
Qinsert(item)
Rear=maxsize-1 Rear=rear+1 Queue[rear]=item
Qinsert(20) -1=5 ? F Rear=-1+1=0 Queue[0]=20
Qinsert(30) 0=5? F Rear= 0+1=1 Queue[1]=30
Qinsert(40) 1=5? F Rear= 1+1=2 Queue[2]=40
If section Else section
1
2
3

8. Maxsize=6, rear=3, front=-1
• Qinsert(item)
• 1.If (rear = maxsize-1 )
• print (“queue overflow”) and return
• 2.Else
• rear = rear + 1
• Queue [rear] = item
20 30 40 50
0 1 2 3 4 5
rear
front
Function call
Qinsert(item)
Rear=maxsize-1 Rear=rear+1 Queue[rear]=item
Qinsert(20) -1=5 ? F Rear=-1+1=0 Queue[0]=20
Qinsert(30) 0=5? F Rear= 0+1=1 Queue[1]=30
Qinsert(40) 1=5? F Rear= 1+1=2 Queue[2]=40
Qinsert(50) 2=5? F Rear= 2+1=3 Queue[3]=50
If section Else section
1
2
3
4

9. Maxsize=6, rear=4, front=-1
• Qinsert(item)
• 1.If (rear = maxsize-1 )
• print (“queue overflow”) and return
• 2.Else
• rear = rear + 1
• Queue [rear] = item
20 30 40 50 60
0 1 2 3 4 5
rear
front
Function call
Qinsert(item)
Rear=maxsize-1 Rear=rear+1 Queue[rear]=item
Qinsert(20) -1=5 ? F Rear=-1+1=0 Queue[0]=20
Qinsert(30) 0=5? F Rear= 0+1=1 Queue[1]=30
Qinsert(40) 1=5? F Rear= 1+1=2 Queue[2]=40
Qinsert(50) 2=5? F Rear= 2+1=3 Queue[3]=50
Qinsert(60) 3=5? F Rear= 3+1=4 Queue[4]=60
If section Else section
1
2
3
4
5

10. Maxsize=6, rear=5, front=-1
• Qinsert(item)
• 1.If (rear = maxsize-1 )
• print (“queue overflow”) and return
• 2.Else
• rear = rear + 1
• Queue [rear] = item
20 30 40 50 60 70
0 1 2 3 4 5
rear
front
Function call
Qinsert(item)
Rear=maxsize-1 Rear=rear+1 Queue[rear]=item
Qinsert(20) -1=5 ? F Rear=-1+1=0 Queue[0]=20
Qinsert(30) 0=5? F Rear= 0+1=1 Queue[1]=30
Qinsert(40) 1=5? F Rear= 1+1=2 Queue[2]=40
Qinsert(50) 2=5? F Rear= 2+1=3 Queue[3]=50
Qinsert(60) 3=5? F Rear= 3+1=4 Queue[4]=60
Qinsert(70) 4=5? F Rear= 4+1=5 Queue[5]=70
If section Else section
1
2
3
4
5
6

11. Maxsize=6, rear=5, front=-1
• Qinsert(item)
• 1.If (rear = maxsize-1 )
• print (“queue overflow”) and return
• 2.Else
• rear = rear + 1
• Queue [rear] = item
20 30 40 50 60 70
0 1 2 3 4 5
rear
front
Function call
Qinsert(item)
Rear=maxsize-1 Rear=rear+1 Queue[rear]=item
Qinsert(20) -1=5 ? F Rear=-1+1=0 Queue[0]=20
Qinsert(30) 0=5? F Rear= 0+1=1 Queue[1]=30
Qinsert(40) 1=5? F Rear= 1+1=2 Queue[2]=40
Qinsert(50) 2=5? F Rear= 2+1=3 Queue[3]=50
Qinsert(60) 3=5? F Rear= 3+1=4 Queue[4]=60
Qinsert(70) 4=5? F Rear= 4+1=5 Queue[5]=70
Qinsert(80) 5=5? T stop
If section Else section
1
2
3
4
5
6
7

12. Maxsize=6, front=-1
rear=5
• Qdelete()
• If (front =rear)
• print “queue empty” and return
• 2. Else
• Front = front + 1
• item = queue [front];
• Return item
20 30 40 50 60 70
0 1 2 3 4 5
rear
front
Function call
Qdelete()
front=rear Front=front+1 Item=Queeue[front]
If section Else section

13. Maxsize=6, front=0
rear=5
• Qdelete()
• If (front =rear)
• print “queue empty” and return
• 2. Else
• Front = front + 1
• item = queue [front];
• Return item
30 40 50 60 70
0 1 2 3 4 5
rear
front
Function call
Qdelete()
front=rear Front=front+1 Item=Queeue[front]
Qdelete() -1 = 5 ? F front=-1+1=0 item=Queue[0]
If section Else section
1
Item=20

14. Maxsize=6, front=1
rear=5
• Qdelete()
• If (front =rear)
• print “queue empty” and return
• 2. Else
• Front = front + 1
• item = queue [front];
• Return item
40 50 60 70
0 1 2 3 4 5
rear
front
Function call
Qdelete()
front=rear Front=front+1 Item=Queeue[front]
Qdelete() -1 = 5 ? F front=-1+1=0 item=Queue[0]
Qdelete() 0 = 5 ? F front=0+1=1 item=Queue[1]
If section Else section
1
Item=30
2

15. Maxsize=6, front=2
rear=5
• Qdelete()
• If (front =rear)
• print “queue empty” and return
• 2. Else
• Front = front + 1
• item = queue [front];
• Return item
50 60 70
0 1 2 3 4 5
rear
front
Function call
Qdelete()
front=rear Front=front+1 Item=Queeue[front]
Qdelete() -1 = 5 ? F front=-1+1=0 item=Queue[0]
Qdelete() 0 = 5 ? F front=0+1=1 item=Queue[1]
Qdelete() 1 = 5 ? F front=1+1=2 item=Queue[2]
If section Else section
1
Item=40
2
3

16. Maxsize=6, front=3
rear=5
• Qdelete()
• If (front =rear)
• print “queue empty” and return
• 2. Else
• Front = front + 1
• item = queue [front];
• Return item
60 70
0 1 2 3 4 5
rear
front
Function call
Qdelete()
front=rear Front=front+1 Item=Queeue[front]
Qdelete() -1 = 5 ? F front=-1+1=0 item=Queue[0]
Qdelete() 0 = 5 ? F front=0+1=1 item=Queue[1]
Qdelete() 1 = 5 ? F front=1+1=2 item=Queue[2]
Qdelete() 2 = 5 ? F front=2+1=3 item=Queue[3]
If section Else section
1
Item=50
2
3
4

17. Maxsize=6, front=4
rear=5
• Qdelete()
• If (front =rear)
• print “queue empty” and return
• 2. Else
• Front = front + 1
• item = queue [front];
• Return item
70
0 1 2 3 4 5
rear
front
Function call
Qdelete()
front=rear Front=front+1 Item=Queeue[front]
Qdelete() -1 = 5 ? F front=-1+1=0 item=Queue[0]
Qdelete() 0 = 5 ? F front=0+1=1 item=Queue[1]
Qdelete() 1 = 5 ? F front=1+1=2 item=Queue[2]
Qdelete() 2 = 5 ? F front=2+1=3 item=Queue[3]
Qdelete() 3 = 5 ? F front=3+1=4 item=Queue[4]
If section Else section
1
Item=60
2
3
4
5

18. Maxsize=6, front=5
rear=5
• Qdelete()
• If (front =rear)
• print “queue empty” and return
• 2. Else
• Front = front + 1
• item = queue [front];
• Return item
0 1 2 3 4 5
rear
front
Function call
Qdelete()
front=rear Front=front+1 Item=Queeue[front]
Qdelete() -1 = 5 ? F front=-1+1=0 item=Queue[0]
Qdelete() 0 = 5 ? F front=0+1=1 item=Queue[1]
Qdelete() 1 = 5 ? F front=1+1=2 item=Queue[2]
Qdelete() 2 = 5 ? F front=2+1=3 item=Queue[3]
Qdelete() 3 = 5 ? F front=3+1=4 item=Queue[4]
Qdelete() 4= 5 ? F front=4+1=5 item=Queue[5]
If section Else section
1
Item=70
2
3
4
5
6

19. Maxsize=6, front=5
rear=5
• Qdelete()
• If (front =rear)
• print “queue empty” and return
• 2. Else
• Front = front + 1
• item = queue [front];
• Return item
0 1 2 3 4 5
rear
front
Function call
Qdelete()
front=rear Front=front+1 Item=Queeue[front]
Qdelete() -1 = 5 ? F front=-1+1=0 item=Queue[0]
Qdelete() 0 = 5 ? F front=0+1=1 item=Queue[1]
Qdelete() 1 = 5 ? F front=1+1=2 item=Queue[2]
Qdelete() 2 = 5 ? F front=2+1=3 item=Queue[3]
Qdelete() 3 = 5 ? F front=3+1=4 item=Queue[4]
Qdelete() 4= 5 ? F front=4+1=5 item=Queue[5]
Qdelete() 5=5? T queue empty - -
If section Else section
1
2
6
7

20. Conditions to be satisfied in Queue
• Queue is empty FRONT=REAR
• Queue is full REAR=Maxsize
• Queue contains element >= 1
FRONT <REAR
NO. OF ELEMENT = REAR-FRONT+1
Disadvantage of Queue: The deleted element’s space in the queuqe
cannot be reused-utilized for inserting another element.

21. Applications of
queues
Queue is
used in BFS.
Queue is
used by OS to
schedule
equal priority
jobs
In recognizing
palindrome
Simulation

22. Representation of Queues
• Queues can be represented using arrays
• Queues can be represented using Linked List

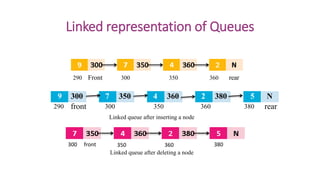
23. Array representation of Queues
12 9 7 18 45
front rear
A[0] A[1] A[2] A[3] A[4]

24. Linked representation of Queues
290 Front 300 350 360 rear
9 300 7 350 4 360 2 380 5 N
290 front 300 350 360 380 rear
Linked queue after inserting a node
300 front 350 360 380
Linked queue after deleting a node

25. Insert an element in queue using linked list
STEP-1: Allocate memory for the new node & name it as TEMP.
STEP-2: SET TEMP➔ DATA = NUM
SET TEMP→ LINK = NULL
STEP-3: IF FRONT = NULL
FRONT=REAR=TEMP
ELSE
REAR→ LINK =TEMP
REAR=TEMP
[ END OF IF]
STEP-4: EXIT
FRONT=REAR=NULL

26. 20 NULL
5000
TEMP
STEP-1: Allocate memory for the new node & name it as TEMP.
STEP-2: SET TEMP➔ DATA = NUM
SET TEMP→ LINK = NULL FRONT=REAR=NULL
1. QINSERT_LINK(TEMP)
Data link

27. STEP-3: IF FRONT = NULL
FRONT=REAR=TEMP
ELSE
REAR→ LINK =TEMP
REAR=TEMP
[ END OF IF]
FRONT=REAR=5000
20 NULL
5000
FRONT REAR

28. 30 NULL
6000
TEMP
STEP-1: Allocate memory for the new node & name it as TEMP.
STEP-2: SET TEMP➔ DATA = NUM
SET TEMP→ LINK = NULL FRONT=REAR=TEMP
2. QINSERT_LINK(TEMP)

29. STEP-3: IF FRONT = NULL
FRONT=REAR=TEMP
ELSE
REAR→ LINK =TEMP
REAR=TEMP
[ END OF IF]
FRONT=5000
REAR=6000
20 NULL
5000
FRONT REAR
30 NULL
6000
TEMP
20 6000
5000
FRONT
REAR
30 NULL
6000
TEMP

30. 40 NULL
7000
TEMP
STEP-1: Allocate memory for the new node & name it as TEMP.
STEP-2: SET TEMP➔ DATA = NUM
SET TEMP→ LINK = NULL
3. QINSERT_LINK(TEMP)
FRONT=5000
REAR=6000

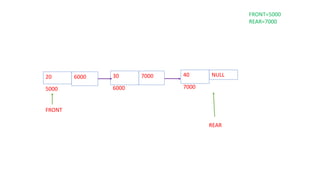
31. STEP-3: IF FRONT = NULL
FRONT=REAR=TEMP
ELSE
REAR→ LINK =TEMP
REAR=TEMP
[ END OF IF]
FRONT=5000
REAR=7000
20 6000
5000
FRONT REAR
30 NULL
6000
20 6000
5000
FRONT REAR
30 7000
6000
40 NULL
7000
TEMP

32. FRONT=5000
REAR=7000
20 6000
5000
FRONT
REAR
30 7000
6000
40 NULL
7000

33. Delete an element in queue using linked list
STEP-1: If FRONT = NULL
write “underflow”
go to step 3.
[End of if]
STEP-2: SET TEMP = FRONT
FRONT=FRONT→ LINK
IF FRONT = NULL
REAR=NULL
STEP-3: EXIT

34. Delete an element in queue using linked list
STEP-1: If FRONT = NULL
write “underflow”
go to step 3.
[End of if]
STEP-2: SET TEMP = FRONT
FRONT=FRONT→ LINK
IF FRONT = NULL
REAR=NULL
STEP-3: EXIT
20 6000
5000
FRONT
REAR
30 7000
6000
40 NULL
7000
1. QDELETE_LINK()
TEMP

35. Delete an element in queue using linked list
STEP-1: If FRONT = NULL
write “underflow”
go to step 4.
[End of if]
STEP-2: SET TEMP = FRONT
FRONT=FRONT→ LINK
IF FRONT = NULL
REAR=NULL
STEP-3: FREE(TEMP)
STEP-4: EXIT
20 6000
5000
FRONT REAR
30 7000
6000
40 NULL
7000
1. QDELETE_LINK()
TEMP
FRONT REAR
30 7000
6000
40 NULL
7000

36. Delete an element in queue using linked list
STEP-1: If FRONT = NULL
write “underflow”
go to step 4.
[End of if]
STEP-2: SET TEMP = FRONT
FRONT=FRONT→ LINK
IF FRONT = NULL
REAR=NULL
STEP-3: FREE(TEMP)
STEP-4: EXIT
2. QDELETE_LINK()
TEMP
FRONT REAR
30 7000
6000
40 NULL
7000
TEMP
FRONT REAR
30 7000
6000
40 NULL
7000
FRONT REAR
40 NULL
7000

37. Delete an element in queue using linked list
STEP-1: If FRONT = NULL
write “underflow”
go to step 4.
[End of if]
STEP-2: SET TEMP = FRONT
FRONT=FRONT→ LINK
IF FRONT = NULL
REAR=NULL
STEP-3: FREE(TEMP)
STEP-4: EXIT
3. QDELETE_LINK()
4. QDELETE_LINK()
FRONT=NULL
REAR=NULL
40 NULL
7000
TEMP
FRONT REAR
40 NULL
7000
TEMP
TEMP

38. Types of Queues
• Dequeue
• Circular Queue
• Priority Queue

39. Dequeues
• Deque stands for double ended queue.
• Elements can be inserted or deleted at either end.
• Also known as head-tail linked list.
34 12 53 61 9
FRONT
Insertion
Deleion
REAR
Insertion
Deleion

40. Types of Dequeues
• Input restricted queue
34 12 53 61 9
FRONT
Deleion
REAR
Insertion
Deleion

41. Types of Dequeues
• Output restricted queue
34 12 53 61 9
FRONT
Deleion
REAR
Insertion
Insertion

42. Circular Queues
• Circular queue are used to remove the drawback of simple queue.
• Both the front and the rear pointers wrap around to the beginning of
the array.
• It is also called as “Ring buffer”.

43. Algorithm CQ_insert(ITEM)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit

44. Algorithm CQ_insert(ITEM)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
FRONT=-1
REAR=-1
MAX=7

45. Algorithm CQ_insert(10)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
10
FRONT=-1
REAR=-1
MAX=7
IF FRONT=-1 & REAR=-1 T
REAR=FRONT=0
IF ((REAR+1)%MAX=FRONT)
(-1+1)%7=-1
0 = -1 F
C1
C2
REAR=(REAR+1)%MAX
FRONT=0
REAR=0
MAX=7
REAR=MAX-1 & FRONT!=0
REAR=0
C3
CQ[REAR]=ITEM
CQ[0]=10

46. Algorithm CQ_insert(20)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
10
FRONT=0
REAR=0
MAX=7
IF FRONT=-1 & REAR=-1 F
REAR=FRONT=0
IF ((REAR+1)%MAX=FRONT)
(0+1)%7= 0
1 = -1 F
C1
C2
REAR=(REAR+1)%MAX
(0+1)%7= 1
FRONT=0
REAR=1
MAX=7
REAR=MAX-1 & FRONT!=0
0=6 F & 0!0 F
REAR=0
C3
CQ[REAR]=ITEM
CQ[1]=20
C4
20

47. Algorithm CQ_insert(30)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
10
FRONT=0
REAR=1
MAX=7
IF FRONT=-1 & REAR=-1 F
REAR=FRONT=0
IF ((REAR+1)%MAX=FRONT)
(1+1)%7= 0
2 = 0 F
C1
C2
REAR=(REAR+1)%MAX
(1+1)%7= 2
FRONT=0
REAR=2
MAX=7
REAR=MAX-1 & FRONT!=0
1=6 F
REAR=0
C3
CQ[REAR]=ITEM
CQ[2]=30
C4
20
30

48. Algorithm CQ_insert(30)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
10
FRONT=0
REAR=1
MAX=7
IF FRONT=-1 & REAR=-1 F
REAR=FRONT=0
IF ((REAR+1)%MAX=FRONT)
(1+1)%7= 0
2 = 0 F
C1
C2
REAR=(REAR+1)%MAX
(1+1)%7= 2
FRONT=0
REAR=2
MAX=7
REAR=MAX-1 & FRONT!=0
1=6 F
REAR=0
C3
CQ[REAR]=ITEM
CQ[2]=30
C4
20
30

49. Algorithm CQ_insert(40)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
10
FRONT=0
REAR=2
MAX=7
IF FRONT=-1 & REAR=-1 F
REAR=FRONT=0
IF ((REAR+1)%MAX=FRONT)
(2+1)%7= 0
3 = 0 F
C1
C2
REAR=(REAR+1)%MAX
(2+1)%7= 3
FRONT=0
REAR=3
MAX=7
REAR=MAX-1 & FRONT!=0
2=6 F
REAR=0
C3
CQ[REAR]=ITEM
CQ[3]=40
C4
20
30
40

50. Algorithm CQ_insert(50)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
10
FRONT=0
REAR=3
MAX=7
IF FRONT=-1 & REAR=-1 F
REAR=FRONT=0
IF ((REAR+1)%MAX=FRONT)
(3+1)%7= 0
4= 0 F
C1
C2
REAR=(REAR+1)%MAX
(3+1)%7= 4
FRONT=0
REAR=4
MAX=7
REAR=MAX-1 & FRONT!=0
4=6 F
REAR=0
C3
CQ[REAR]=ITEM
CQ[4]=50
C4
20
30
40
50

51. Algorithm CQ_insert(60)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
10
FRONT=0
REAR=4
MAX=7
IF FRONT=-1 & REAR=-1 F
REAR=FRONT=0
IF ((REAR+1)%MAX=FRONT)
(4+1)%7= 0
5= 0 F
C1
C2
REAR=(REAR+1)%MAX
(4+1)%7= 5
FRONT=0
REAR=5
MAX=7
REAR=MAX-1 & FRONT!=0
5=6 F
REAR=0
C3
CQ[REAR]=ITEM
CQ[5]=60
C4
20
30
40
50
60

52. Algorithm CQ_insert(70)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
10
FRONT=0
REAR=5
MAX=7
IF FRONT=-1 & REAR=-1 F
REAR=FRONT=0
IF ((REAR+1)%MAX=FRONT)
(5+1)%7= 0
6= 0 F
C1
C2
REAR=(REAR+1)%MAX
(5+1)%7= 6
FRONT=0
REAR=6
MAX=7
REAR=MAX-1 & FRONT!=0
5=6 F
REAR=0
C3
CQ[REAR]=ITEM
CQ[6]=70
C4
20
30
40
50
60
70

53. Algorithm CQ_insert(80)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
10
FRONT=0
REAR=6
MAX=7
IF ((REAR+1)%MAX=FRONT)
(6+1)%7= 0
0= 0 T
C1
20
30
40
50
60
70

54. Algorithm CQ_insert(80)
• Step-1: If (REAR+1)%MAX=FRONT
• Write Overflow
• GoTo Step 4.
• [End of if]
• Step-2: If FRONT=-1 and REAR =-1
• REAR=FRONT=0
• Else If REAR=MAX-1 AND FRONT!=0
• REAR=0
• Else
• REAR=(REAR+1)%MAX
• [End of If]
• Step-3: CQ[REAR]=ITEM
• Step-4: Exit
CQ[0]
CQ[1]
CQ[2]
CQ[3]
CQ[4]
CQ[5]
CQ[6]
REAR
FRONT
IF FRONT=-1 & REAR=-1 F
REAR=FRONT=0
IF ((REAR+1)%MAX=FRONT)
(6+1)%7= 1
0= 1 F
C1
C2
REAR=(REAR+1)%MAX
FRONT=1
REAR=6
MAX=7
REAR=MAX-1 & FRONT!=0
6=6 T & 1!0 T
REAR=0
C3
CQ[REAR]=ITEM
CQ[0]=80
C4
20
30
40
50
60
70
CQ_delete()
80

55. Algorithm CQ_delete()
• Step-1: If FRONT=-1
• Write Underflow
• go to step 4
• [End of if]
• Step-2: VAL=CQ[FRONT]
• Step-3:If FRONT = REAR
• REAR=FRONT=-1
• Else If FRONT=MAX-1
• FRONT=0
• Else
• FRONT=FRONT+1
• [End of If]
• Step-4: Exit
CQ[0]
CQ[1]
CQ[3]
CQ[5]
CQ[6]
REAR
FRONT
10 20
30
40
50
60
CQ[2]
70