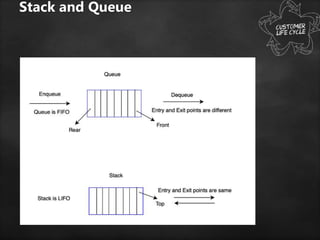
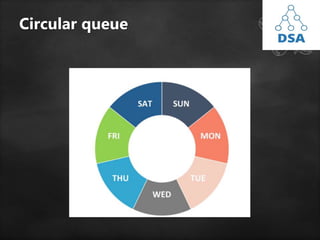
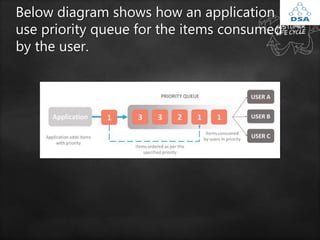
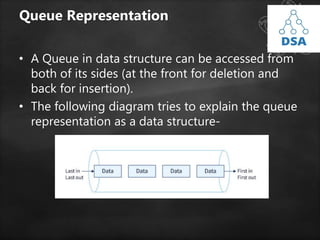
This document provides a detailed overview of queues and linked lists in data structures, focusing on queue operations, representations, implementations, and types. It explains FIFO principles, various operations (enqueue, dequeue, peek), and how to implement a queue using arrays or stacks. Additionally, it discusses practical applications of queues and different types, including simple queues, circular queues, priority queues, and double-ended queues.

1. Data Structure & Algorithm
Unit 2: Queue and Linked List
by:
Dr. Shweta Saraswat

2. Contents
Part A: Queue
• Basic Queue Operations,
• Representation of a Queue using array,
• Implementation of Queue Operations using
Stack,
• Applications of Queues-
• Round Robin Algorithm.
• Circular Queues,
• DeQueue Priority Queues.

3. What is queue?
• The Queue in data structure is an ordered, linear
sequence of items.
• It is a FIFO (First In First Out) data structure, which
means that we can insert an item to the rear end of
the queue and remove from the front of the queue
only.
• A Queue is a sequential data type, unlike an array,
in an array, we can access any of its elements using
indexing, but we can only access the element at the
front of the queue at a time.

4. Queue

5. Example
• A queue of people waiting for their turn or a queue
of airplanes waiting for landing instructions are also
some real life examples of the queue data structure.
• In the above illustration, we can see that the person
standing at the front of the queue will be the first
one to leave the queue and the person standing at
the last of the queue will be the last one to leave.

6. Queue Representation
• A Queue in data structure can be accessed from
both of its sides (at the front for deletion and
back for insertion).
• The following diagram tries to explain the queue
representation as a data structure-

7. Queue Operations

8. Working of Queue
• We can use queue to perform its main two
operations:
• Enqueue and Dequeue,
• other operations being Peek, isEmpty and isFull.

9. Enqueue
The Enqueue operation is used to add an element
to the front of the queue.
Steps of the algorithm:
• Check if the Queue is full.
• Set the front as 0 for the first element.
• Increase rear by 1.
• Add the new element at the rear index.

10. Dequeue
The Dequeue operation is used to remove an
element from the rear of the queue.
Steps of the algorithm:
• Check if the Queue is empty.
• Return the value at the front index.
• Increase front by 1.
• Set front and rear as -1 for the last element.

11. Peek
The Peek operation is used to return the front
most element of the queue.
• Steps of the algorithm:
• Check if the Queue is empty.
• Return the value at the front index.

12. isFull
The isFull operation is used to check if the queue
is full or not.
Steps of the algorithm:
• Check if the number of elements in the queue
(size) is equal to the capacity, if yes, return True.
• Return False.

13. isEmpty
The isEmpty operation is used to check if the
queue is empty or not.
Steps of the algorithm:
• Check if the number of elements in the queue
(size) is equal to 0, if yes, return True.
• Return False.

14. Queue Implementation

15. • A Queue in data structure can be implemented
using arrays, linked lists, or vectors. For the
sake of simplicity, we will be implementing
queue using a one-dimensional array.

16. To implement a queue using an array,
• create an array arr of size n and
• take two variables front and rear both of which
will be initialized to 0 which means the queue is
currently empty.
• Element
– rear is the index up to which the elements are stored
in the array and
– front is the index of the first element of the array.

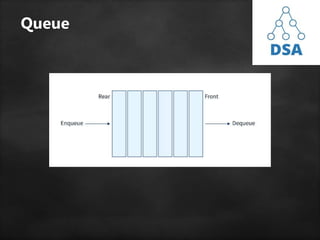
17. Now, some of the implementations of queue
operations are as follows:
• Enqueue: Addition of an element to the queue. Adding an
element will be performed after checking whether the queue
is full or not. If rear < n which indicates that the array is not
full then store the element at arr[rear] and increment rear by 1
but if rear == n then it is said to be an Overflow condition as
the array is full.
• Dequeue: Removal of an element from the queue. An
element can only be deleted when there is at least an element
to delete i.e. rear > 0. Now, the element at arr[front] can be
deleted but all the remaining elements have to shift to the left
by one position in order for the dequeue operation to delete
the second element from the left on another dequeue
operation.
• Front: Get the front element from the queue i.e. arr[front] if
the queue is not empty.
• Display: Print all elements of the queue. If the queue is non-
empty, traverse and print all the elements from the index front
to rear.

18. Implementation of Queue
Operations using Stack

19. Understanding the Problem:
• Queue and Stack are both different data
structures with different properties and also
different use cases. However, the given problem
is asking to implement one data structure, i.e.,
Queue, with the help of the other (Stack). Let us
first look at the features and characteristics of
Stack and Queue and try to get an idea of how
we can implement them with the help of each
other.

20. Stack and Queue

21. Stack and Queue
• Stack is a LIFO based data structure and there is
only one side in Stack(top) acting as entry and
exit point in Stacks.
• Stack supports operations like Push, Pop, Peek
and isEmpty.
• Queue is a FIFO based data structure and there
are two different points, one for entry and the
other one for exit.
• Queue supports operations like enqueue,
dequeue, peek and isEmpty.

22. Solution
• We can implement Queue using two Stacks. Two
Stacks taken together can help us to get all the
operations as supported by Queue. All the use-
cases of queue can be achieved by using two
stacks.

23. Possible questions to ask the interviewer:
→
• Implementation of Queue using Stack can make
one of the operation costly(enqueue or
dequeue). Which operation needs to be less
complex?
• ( Ans: You can choose either of the operation.)
• By making enqueue operation costly: We will
try to insert in a way such that the first element
inserted is at the top of the stack.
• By making dequeue operation costly: In this,
we try to optimize the enqueue operation but
the dequeue operation becomes costly.

24. Modifying the Enqueue Operation
• The idea here is to modify the insertion
operation of the Queue so that it can be
implemented using Stacks. Since in a queue the
element which gets in first, gets out first so when
using stack we have to figure out a way so that
the element inserted first should present at the
top of the stack. For this during insertion, we will
use a second stack to push everything from the
first stack into the second one and then push the
element to be inserted into the first one then
again all the elements from the second stack will
be pushed to the first one. This way the insertion
is costly but we can get a queue using stack.

25. Solution steps
Algorithm for Insertion
• Take two stacks S1 and S2
• If S1 is empty, insert directly into S1.
• If S1 is not empty, push all the elements from S1
to S2.
• Push the element to be inserted into S1.
• Push everything from S2 back to S1.
Algorithm for Deletion
• Pop-out the element from S1 if S1 is not empty.
• If S1 is not empty, return -1.

26. Modifying the Enqueue Operation
• Complexity AnalysisTime Complexity :
O(N) for Insertion , O(1) for Deletion .
• Space Complexity : O(N)

27. Modifying the Dequeue Operation
Solution idea
• Here we modifying the deletion or the dequeue
operation of the queue. This will lead to the
dequeue operation being more costly but it will
help in implementing queue with stacks. For
deleting we first need to check if both the
stacks(as we are using two) are not empty and if
this condition is true, we will simply move all the
elements from stack S1 to stack S2.
• This will let the first element inserted into the
stack to be at the top. We will then perform a
pop operation on stack S2.

28. Solution steps
Algorithm for Insertion
• Take two stacks S1 and S2.
• Push everything to S1 taking into consideration
that S1 has unlimited size.
Algorithm for Deletion
• If both S1 and S2 is empty return -1.
• Push everything to S2 from S1.
• Delete(pop) the top element from S2.

29. Complexity Analysis
• Time Complexity : O(N) for dequeue and
O(1) for enqueue.
• Space Complexity : O(N)

30. Applications of Queue

31. Some of the Application of Queue in Data
Structure
Here are some of the common application of queue in data
structure:
• Queues can be used to schedule jobs and ensure that
they are executed in the correct order.
• Queues can be used to manage the order in which print
jobs are sent to the printer.
• Queues are used to implement the breadth-first search
algorithm.
• Queues can be used to manage incoming calls and
ensure that they are handled in the correct order.
• Queues can be used to manage the order in which
processes are executed on the CPU.
• Queues can be used for buffering data while it is being
transferred between two systems. When data is received,
it is added to the back of the queue, and when data is
sent, it is removed from the front of the queue.

32. Types of Queues in Data
Structure

33. Types of Queues in Data Structure
There are four different types of queues in data
structures:
• Simple Queue
• Circular Queue
• Priority Queue
• Double-Ended Queue (Deque)

34. Simple Queue
• It is the most basic queue in which the insertion
of an item is done at the front of the queue and
deletion takes place at the end of the queue.
• Ordered collection of comparable data kinds.
• Queue structure is FIFO (First in, First Out).
• When a new element is added, all elements
added before the new element must be deleted
in order to remove the new element.

35. Circular Queue
• A circular queue is a special case of a
simple queue in which the last member is linked
to the first. As a result, a circle-like structure is
formed.
• The last node is connected to the first node.
• Also known as a Ring Buffer as the nodes are
connected end to end.
• Insertion takes place at the front of the queue
and deletion at the end of the queue.
• Circular queue application: Insertion of days in
a week.

36. Circular queue

37. Priority Queue
In a priority queue, the nodes will have some
predefined priority in the priority queue. The
node with the least priority will be the first to be
removed from the queue. Insertion takes place in
the order of arrival of the nodes.
Some of the applications of priority queue:
• Dijkstra’s shortest path algorithm
• Prim’s algorithm
• Data compression techniques like Huffman code

38. Below diagram shows how an application
use priority queue for the items consumed
by the user.

39. Deque (Double Ended Queue)
• In a double-ended queue, insertion and deletion
can take place at both the front and rear ends of
the queue.

40. Thank you