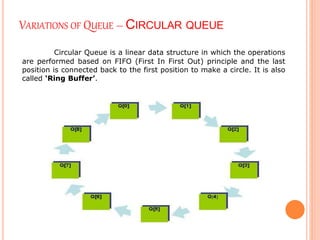
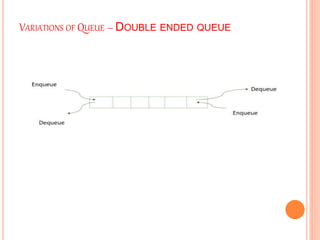
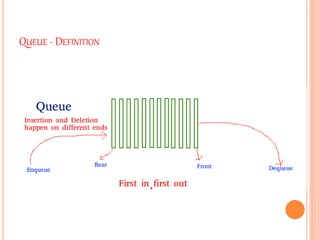
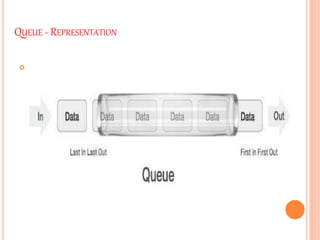
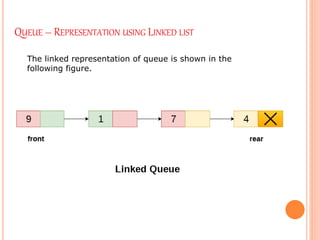
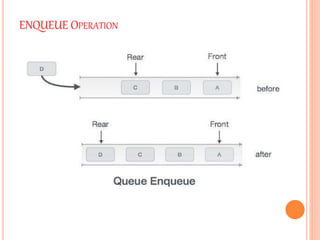
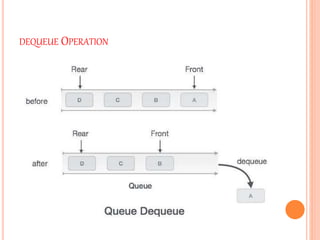
This document discusses queues, including: 1. Queues follow a First-In First-Out (FIFO) methodology where the first item stored is the first item accessed. 2. Queues can be implemented using arrays or linked lists, with two pointers - a front pointer and rear pointer - to keep track of the first and last elements. 3. The basic queue operations are enqueue, which adds an item to the rear, and dequeue, which removes an item from the front.

1. QUEUE AND ITS OPERATIONS
Mrs.G.Chandraprabha,M.Sc.,M.Phil.,
Assistant Professor,
Department of Information Technology,
V.V.Vanniaperumal College for Women,
Virudhunagar.

2. QUEUE - INTRODUCTION
 Queue is an abstract data structure, somewhat similar to
Stacks.
 Unlike stacks, a queue is open at both its ends. One end is
always used to insert data (enqueue) and the other is used to
remove data (dequeue).
 Queue follows First-In-First-Out methodology, i.e., the data
item stored first will be accessed first.

3. QUEUE - DEFINITION
 A Queue is a linear structure which follows a particular order
in which the operations are performed.
 The order is First In First Out (FIFO).
 A good example of a queue is any queue of consumers for a
resource where the consumer that came first is served first.
 The difference between stack and queues is in removing.
 In a stack we remove the item the most recently added; in a
queue, we remove the item the least recently added.

4. QUEUE - DEFINITION

5. QUEUE - EXAMPLE

6. QUEUE - REPRESENTATION
 As we now understand that in queue, we access both ends for
different reasons.
 As in stacks, a queue can also be implemented using Arrays,
Linked-lists, Pointers and Structures.
 For the sake of simplicity, we shall implement queues using
one-dimensional array.

7. QUEUE - REPRESENTATION


8. QUEUE – REPRESENTATION USING ARRAY
 Array is the easiest way to implement a queue. Queue can be also
implemented using Array

 In the above diagram, Front and Rear of the queue point at the first index of the
array. (Array index starts from 0).
 While adding an element into the queue, the Rear keeps on moving ahead and
always points to the position where the next element will be inserted. Front
remains at the first index.

9. QUEUE – REPRESENTATION USING LINKED LIST
 In the linked queue, there are two pointers maintained in
the memory i.e. front pointer and rear pointer. The front
pointer contains the address of the starting element of
the queue while the rear pointer contains the address of
the last element of the queue.
 Insertion and deletions are performed at rear and front
end respectively. If front and rear both are NULL, it
indicates that the queue is empty.

10. QUEUE – REPRESENTATION USING LINKED LIST
The linked representation of queue is shown in the
following figure.

11. OPERATIONS ON QUEUE
 Queue operations may involve initializing or defining the
queue, utilizing it, and then completely erasing it from the
memory. Here we shall try to understand the basic
operations associated with queues .
 enqueue() − add (store) an item to the queue.
 dequeue() − remove (access) an item from the queue.
 Few more functions are required to make the above-
mentioned queue operation efficient. These are −
 peek() − Gets the element at the front of the queue
without removing it.
 isfull() − Checks if the queue is full.
 isempty() − Checks if the queue is empty.
 In queue, we always dequeue (or access) data, pointed
by front pointer and while enqueing (or storing) data in
the queue we take help of rear pointer.

12. ENQUEUE OPERATION
 Queues maintain two data pointers, front and rear.
Therefore, its operations are comparatively difficult to
implement than that of stacks.
 The following steps should be taken to enqueue (insert)
data into a queue −
 Step 1 − Check if the queue is full.
 Step 2 − If the queue is full, produce overflow error and
exit.
 Step 3 − If the queue is not full, increment rear pointer to
point the next empty space.
 Step 4 − Add data element to the queue location, where
the rear is pointing.
 Step 5 − return success.

13. ENQUEUE OPERATION

14. ENQUEUE OPERATION – ARRAY ALGORITHM
procedure enqueue(data)
if queue is full
return overflow
endif
rear ← rear + 1
queue[rear] ← data
return true
end procedure

15. DEQUEUE OPERATION
 Accessing data from the queue is a process of two tasks
− access the data where front is pointing and remove
the data after access. The following steps are taken to
perform dequeue operation −
 Step 1 − Check if the queue is empty.
 Step 2 − If the queue is empty, produce underflow error
and exit.
 Step 3 − If the queue is not empty, access the data
where front is pointing.
 Step 4 − Increment front pointer to point to the next
available data element.
 Step 5 − Return success.

16. DEQUEUE OPERATION

17. DEQUEUE OPERATION – ARRAY ALGORITHM
procedure dequeue
if queue is empty
return underflow
end if
data = queue[front]
front ← front + 1
return true
end procedure

18. VARIATIONS OF QUEUE – CIRCULAR QUEUE
Circular Queue is a linear data structure in which the operations
are performed based on FIFO (First In First Out) principle and the last
position is connected back to the first position to make a circle. It is also
called ‘Ring Buffer’.

19. VARIATIONS OF QUEUE – DOUBLE ENDED QUEUE
oDouble Ended Queue is also a Queue data structure in
which the insertion and deletion operations are performed at
both the ends (front and rear).
oThat means, we can insert at both front and rear positions
and can delete from both front and rear positions.
oSince Dequeue supports both stack and queue operations,
it can be used as both.
oThe Dequeue data structure supports clockwise and
anticlockwise rotations in O(1) time which can be useful in
certain applications.
oAlso, the problems where elements need to be removed
and or added both ends can be efficiently solved using
Dequeue.

20. VARIATIONS OF QUEUE – DOUBLE ENDED QUEUE

21. THANKYOU