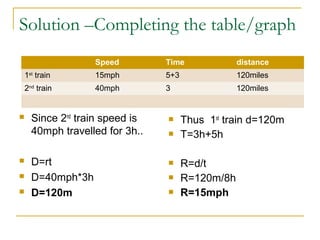
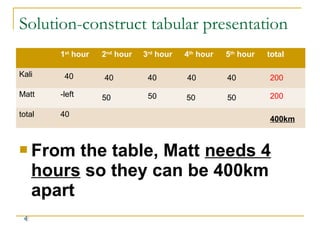
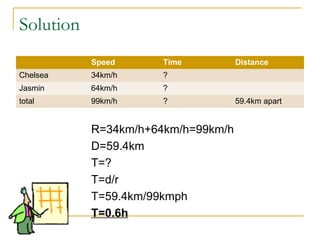
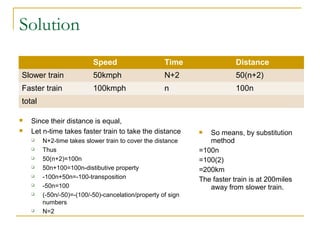
This document discusses speed, time, and distance formulas. It explains that these formulas relate time, distance, and speed, and have practical applications for calculating travel times, distances, and speeds. The key formulas presented are: Distance = Rate x Time Rate = Distance / Time Time = Distance / Rate Steps for solving problems using these formulas are outlined, including translating the question into mathematical terms, putting values into consistent units, writing the appropriate equation, and solving it. Several example problems are worked through to demonstrate applying the formulas to calculate distances, rates, and times for scenarios involving traveling cars, trains, runners, and planes.

1. Speed, Time and Distance
Formulas
Boyet B. Aluan
San Roque Elementary School

2. What are Time and Distance formulas?

Time and Distance
Formulas relate time,
distance, and speed.
These relationships
have many practical
applications.

3. Why do you need to know the Speed,
Time and Distance Formula?
 To
figure how long a trip will
take
 To see how far you can go in
a set amount of time
 To see how fast you took a trip
 To compare different trips

4. Steps in solving Speed, Time and Distance
Formulas
 Step
1. Translate the question
into mathematical terms. For
example, if you are asked miles
per hour, write the question as
miles divided by hours.
 Ex m/h or mph

5. Steps in solving Speed, Time and Distance
Formulas
 Step
2. Put everything in
constant units. For example, if
the question asks miles per
hour, every time must be placed
in terms of hours, and every
distance must be placed in
terms of miles.

6. Conversion Units
Remember: There are 60 seconds in
a minute, 60 minutes in an hour, and
24 hours in a day.
 Remember: There are 12 inches in a
foot, 3 feet in a yard, and 5280 feet in
a mile.


7. Time Conversions






To convert minutes to hours, divide by 60.
To convert hours to minutes, multiply by 60
To convert seconds to minutes, divide by 60
To convert minutes to seconds, multiply by
60
To convert days to hours, multiply by 24
To convert hours to days, divide by 24

8. Measurement Conversions




To convert inches to feet, divide by 12
To convert feet to inches, multiply by 12
To convert feet to miles, divide by 5280
To convert miles to feet, multiply by 5280

9. Step 3. Write the equation you want
to solve.
 Use the correct formula to solve it.
 Be careful about what you multiply,
and what you divide!


10. What are the basic formulas?
Distance = Rate * Time (d = r * t)
 Rate = Distance / Time (r =d/ t)
 Time = Distance / Rate (t = d / r)

Be sure you use the right formula!

11. To find distance

Distance = Rate * Time (d = r * t)
For example, to find miles, multiply miles per
hour (rate) times the number of hours.
Miles = Miles x Hours
Hours
The hours cancel, you are left with miles.

12. To find the rate of speed
 Rate
= Distance /Time (r =d/ t)
rate- constant/ average
speed. To find miles per hour,
divide miles driven by the
number of hours driven.

13. To find the time it takes to travel.

Time = Distance / Rate (t = d / r)
Hours = Miles_____
Miles/Hour
Remember, to divide fractions, flip and multiply
Hours = Miles x Hours
Miles
Miles cancel, you are left with hours

14. Quiz 1-finding the distance
A
girl cycles for 3h at a
speed of 40 km/h. what is
the distance did she
travel?

15. Step one
 Put
in constant units
 Rate was given in km/h,

16. Question 1
What formula should be used?

We are looking for distance so use
Answer
 A. d=r*t
 B. r=d/t
 C. t=d/r

17. Solve
D=rt
D=?
R=40km/h
T=3hrs
Substitute the value
D=rt
D=40km/h(3h)
Cancel h
D=120km

18. Quiz2 finding the time
A
train travels at a speed of
30mph and travel a distance of
240 miles. How long did it take
the train to complete its
journey?

19. Question 1
What formula should be used?

We are asked to find how long did it
take the train to complete its journey so
used
Answer
 A. d=rt
 B. r=d/t
 C. t=d/r

20. Solve
T=d/r
T=?
R= 30mph
D=240m
T= 240M/30mph
Cancel m(miles)
T=8h is the time to complete the
journey

21. Quiz 3

A car travels a distance
of 540km in 6 hours.
What is the speed did it
travel at?

22. Question 3

We are asked to find the rate to travel the
distance of 540km in 6 hours. What
formula should be used?
Answer
 A. d=rt
 B. r=d/t
 C. t=d/r

23. Solution
R=d/t
R=?
D= 540 m
T=6h
Substitute:
R=d/t
R=(540m)/6h
R=90mph

24. Quiz4
John is a runner. He runs the
100m sprint in 10.6s. What speed
did he travel at?
The unit is (m/s)
Use r=d/t where r=?, t=10.6s,
d=100meter
Substitute
R=(100m)/10.6s
R= 9.43m/s

25. Quiz 5

At 11:00 am, a car(1) leaves
city “A” at a constant rate of
60m/h toward city “B”. At the
same time a second car(2)
leaves city “B” toward city “A”
at the constant speed of
50mph. The distance between
city A and B is 220miles and
these cities are connected by a
highway used by the two cars.
At what time will the two cars
cross each other?

26. Solution -construct a tabular
presentation
Speed (R)
Car 1
110mph
?
220m
50mph
total
Distance (D)
60mph
car2
TIME (T)
T=d/t
T=220m/110mph
T=2h
So at constants speed, cars cross each other at
1:00pm

27. Quiz 6

Kali left school and traveled toward
her friend’s house at an average
speed of 40km/h. Matt left one hour
later and traveled in the opposite
direction with an average speed of
50km/h. find the number of hours
Matt needs to travel before they are
400km apart.

28. Solution-construct tabular presentation
1st hour
Kali
40
Matt
-left
total
40
 From
2nd hour
40
50
3rd hour
4th hour
5th hour
total
40
40
40
200
50
50
50
200
400km
the table, Matt needs 4
hours so they can be 400km
apart

29. Quiz 7

Chelsea left the White House and
traveled toward the capital at an
average speed of 34km/h. Jasmine left
at the same time traveled in the
opposite direction with an average
speed of 65km/h. Find the number of
hours Jasmine needs to travel before
they are 59.4 km apart.

30. Solution
Speed
Time
Chelsea
34km/h
?
Jasmin
64km/h
?
total
99km/h
?
R=34km/h+64km/h=99km/h
D=59.4km
T=?
T=d/r
T=59.4km/99kmph
T=0.6h
Distance
59.4km apart

31. Quiz 8

A train leaves Deb’s house and travels
at 50mph. Two hours later, another
train leaves from Deb’s house on the
track beside or parallel to the first train
but it travels at 100mph. How far away
from Deb’s house will the faster train
pass the other train?

32. Solution
Speed
Time
Distance
Slower train
50kmph
N+2
50(n+2)
Faster train
100kmph
n
100n
total


Since their distance is equal,
Let n-time takes faster train to take the distance








N+2-time takes slower train to cover the distance
Thus
50(n+2)=100n
50n+100=100n-distibutive property
-100n+50n=-100-transposition
-50n=100
(-50n/-50)=-(100/-50)-cancelation/property of sign
numbers
N=2
So means, by substitution
method
=100n
=100(2)
=200km
The faster train is at 200miles
away from slower train.


33. Quiz 9

A train left Chicago and traveled towards
Dallas. Five hours later another train left
for Dallas traveling at 40mph with a goal
or catching up with the first train bounded
for Dallas. The second train finally caught
up with the first train after traveling for
three hours. How fast was the train that
left first going?

34. Solution –Completing the table/graph
Speed


15mph
5+3
120miles
2nd train

distance
1st train

Time
40mph
3
120miles
Since 2nd train speed is
40mph travelled for 3h..
D=rt
D=40mph*3h
D=120m





Thus 1st train d=120m
T=3h+5h
R=d/t
R=120m/8h
R=15mph

35. Quiz 10.Catching up same direction,
has equal distance!

A jet took off Toronto, heading west at a
speed of 405mph. Another jet left for Toronto
from the same airport sometime after the first
jet took off and it was traveling at a speed of
486mph. Ten hours later, the second jet
caught up with the first jet. How long did the
jet fly before the second jet caught up?

36. Solution
Speed




405mph
n+10
405(n+10)
Jet2

Distance
Jet1

Time
486mph
10h
4860mph
405(n+10)=4860
405n+4050=4860
405n=4860-4050
405n=810
405n/(405)=810/(405)
N= 2





So n+10
=2+10
=12
Time =12h
1st jet took 12h before it
just get caught.

37. Thanks!!!
Boyet B. Aluan